What is structural analysis?

Structural analysis is a process in which the effects of different loads and internal forces, acting on structures and their elements are determined. This method of analysis is effective in detecting the failure loads of the structural elements and the design can be altered before commencing the construction process, which ensures proper strength and safety of the structures.

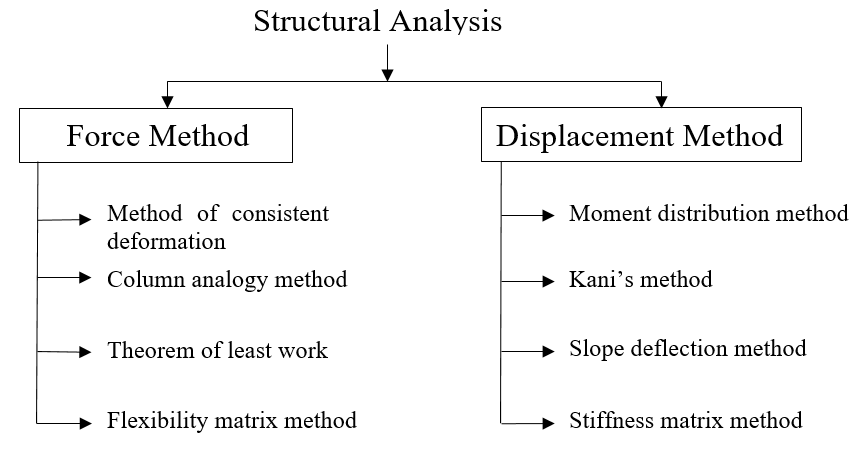
Force method for structural analysis

In this method, the forces are treated as unknown. Compatibility equations are formed for displacements and rotations. Redundant forces are solved from these equations, following which, remaining unknown reactions are computed from equilibrium equations. The different force methods are the flexibility matrix method (it is a matrices method), the theorem of least work, the column analogy method, and the method of consistent deformation.

Displacement method for structural analysis

In this method, the displacements are treated as unknown. From the force-displacement relationships, the unknown displacements are computed, and using force equilibrium relationships, the remaining forces are calculated. This method is the most used structural analysis method. The displacement methods of structural analysis are the moment distribution method, the Kani’s method, the slope deflection method, and the stiffness matrix method (it is one of the matrices methods).

Matrix algebra method for structural analysis

Matrix algebra is a method used for the analysis of structures that are indeterminate to a large extent. There are two types of matrices, namely, the flexibility matrix method and the stiffness matrix method.

Flexibility matrix method for structural analysis

Flexibility is defined as the displacement under a unit load. This flexibility matrix algebra method is a type of finite element method which provides numerical solutions to the differential equations (flexibility matrix represents the linear equations) of the matrices. These equations are then solved to get the member forces. This method of matrix algebra can be used to analyze the beams, portal frames, and pin-jointed trusses (plane trusses).

$$\begin{gathered} F=\frac{∆}{P} \\ where, \\ ∆=Displacement, \\ P=Load \end{gathered}$$ 

Properties of flexibility matrix

1. The flexibility matrix is a square symmetrical matrix.
2. All the elements of the matrix are in terms of slope and displacement.
3. The diagonal elements of the matrix are non-zero and non-negative.
4. The flexibility matrix can be drawn only for stable structures.
5. The order of the flexibility matrix is equal to the degree of static determinacy of the structure.
6. All the elements of the flexibility matrix are denoted by $\left[\begin{array}{c}{F}_{\mathrm{ij}}\end{array}\right]$, where $i$ represents the direction of displacement and $j$ represents the direction of unit load.

$Flexibility matrix, \left[F_{ij}\right]=\left[\begin{array}{cccc}{F}_{11}& F_{12}& ...& F_{1n}\\ F_{21}& F_{22}& ...& F_{2n}\\ ...& ...& ...& ...\\ F_{n1}& F_{n2}& ...& F_{nn}\end{array}\right]$

The first step is to determine the static indeterminacy, then the redundant is chosen and the coordinates are assigned to the redundant force directions. The restraints of the redundant forces are removed to get the basic determinate structure. The deflections due to the given loading in the basic determinate structure in the coordinate directions are determined, from this flexibility matrix is formed. Applying the compatibility conditions and knowing the redundant forces, the member forces are computed.

Stiffness matrix method for structural analysis

Stiffness is defined as the force required to produce unit displacement. This stiffness matrix algebra method is a type of finite element method which provides numerical solutions to the differential equations (stiffness matrix represents the linear equations) of the matrices. The stiffness method is a modified slope-deflection method where matrices are used to construct equations, these equations are then solved to get the member forces. This method of matrix algebra can be used to analyze continuous beams, portal frames, and pin-jointed plane trusses. In the case of truss analysis, the number of unknowns should not be greater than three.

$$\begin{gathered} K=\frac{P}{\Delta } \\ where, \\ P=Load \\ \Delta =Displacement \end{gathered}$$

Properties of Stiffness matrix

1. 1. A stiffness matrix is a square symmetrical matrix.
   2. Diagonal elements are always positive and non-zero.
   3. A stiffness matrix can be drawn for only stable structures.
   4. The Order of the stiffness matrix is equal to the degree of kinematic indeterminacy.
   5. All the elements of the stiffness matrix are forces or moments.
   6. All the elements of the flexibility matrix are denoted by $\left[\begin{array}{c}{K}_{ij}\end{array}\right]$, where $i$ represents the direction of force or moment and $j$ represents  the direction of displacement.

$$\begin{gathered} From slope-deflection equation, \\ {M}_{AB}={\overline{M}}_{AB}+\frac{4EI{\theta }_A}{L}+\frac{2EI{\theta }_B}{L}-\frac{6EI\delta }{L^2} \\ {M}_{BA}={\overline{M}}_{BA}+\frac{4EI{\theta }_B}{L}+\frac{2EI{\theta }_A}{L}-\frac{6EI\delta }{L^2} \\ where, \\ {\overline{M}}_{AB}= Fixed end moment at A \\ {\overline{M}}_{BA}=Fixed end moment at B \\ E=Modulus of Elasiticity \\ I= Moment of inertia \\ {\theta }_A,{\theta }_B=Slopes at A and B \\ \delta =Displacement \end{gathered}$$

$$\begin{gathered} \left[\begin{array}{c}M\end{array}\right]=\left[\begin{array}{c}\overline{M}\end{array}\right]+\left[\begin{array}{c}K\end{array}\right]\left[\begin{array}{c}P\end{array}\right] \\ \left[\begin{array}{c}{M}_{AB}\\ M_{BA}\end{array}\right]=\left[\begin{array}{c}{\overline{M}}_{AB}\\ {\overline{M}}_{BA}\end{array}\right]+\left[\begin{array}{ccc}\frac{4EI}{L}& \frac{2EI}{L}& \frac{-6EI}{L^2}\\ \frac{2EI}{L}& \frac{4EI}{L}& \frac{-6EI}{L^2}\end{array}\right]\left[\begin{array}{c}{\theta }_A\\ {\theta }_B\\ \delta \end{array}\right] \end{gathered}$$

The first step is to find the degree of kinematic indeterminacy n, from this, the coordinate numbers are assigned to the displacements that are unknown. The restraints are added to the structure in all the coordinate directions and the forces developed in the resulting structure are determined. The stiffness matrix is formed by giving a unit displacement to the structure and the resulting forces are determined in all the coordinate directions. On solving the stiffness equations, the displacements are obtained in all the coordinate directions and from these displacements, the member force calculation is done.

Relationship between flexibility matrix and stiffness matrix

Stiffness is the inverse of flexibility and vice-versa.

$$\begin{gathered} Stiffness \propto \frac{1}{Flexibility} \\ \left[\begin{array}{c}K\end{array}\right]={\left[\begin{array}{c}F\end{array}\right]}^{-1} \end{gathered}$$

For instance, In the case of a beam, the stiffness is very high and its flexibility is very less due to the rigid nature of the beam. In the case of a spring, stiffness is very less and flexibility is very high.

Context and Applications

Matrix algebra for structural analysis is a topic that has a wide range of usage in structural and construction engineering. It will be a major part of the following engineering disciplines.

• Bachelors of Technology in Civil Engineering
• Bachelors of Technology in Structural Engineering
• Masters of Technology in Civil Engineering
• Masters of Technology in Structural Engineering

Practice Problems

1. What does the Flexibility coefficients F_ij indicate?

1. Displacement at i due to unit load at j
2. Displacement at j due to unit load at i
3. Force at i due to unit load at j
4. Force at j due to unit load at i

Answer: Option a

Explanation: F_ij is an element of the matrix in which the displacement in the direction i, is due to unit load in the direction j.

2. Which of the following statement is true regarding the matrix methods?

1. Flexibility matrix is a displacement method
2. Stiffness matrix is a displacement method
3. The order of the flexibility matrix is equal to the degree of kinematic indeterminacy
4. The order of the stiffness matrix is equal to the degree of static indeterminacy

Answer: Option b

Explanation: Stiffness matrix is a displacement method. The other statements are false because the flexibility matrix method is a force method of analysis. Similarly, the order of the stiffness matrix is equal to the degree of kinematic indeterminacy and the order of flexibility matrix is equal to the degree of static indeterminacy.

3. What should be the diagonal elements in the matrix method of analysis?

1. Non-negative and non-zero
2. Negative and zero
3. Non-negative and zero
4. Negative and non-zero

Answer: Option a

Explanation: From the properties of the stiffness matrix and flexibility matrix, we know that the diagonal elements of the matrices must be non-negative and non-zero.

4. All the elements of the stiffness matrix are-

1. Slopes and displacements
2. Forces and moments
3. Slope
4. Displacement

Answer: Option b

Explanation: All the elements of the stiffness matrix are forces or moments.

5. What is the structure which is formed by removing all the restraints in the flexibility matrix method of structural analysis called?

1. Basic determinate structure
2. Redundant structure
3. Both a and b
4. None of the above

Answer: Option c

Explanation: In the flexibility matrix method, the structure which is formed by removing all the restraints, is called a basic determinate structure or redundant structure.