What is Mechanics of Solids?
It is the study of the behavior of solid materials, their characteristics under various circumstances such as variation in external forces, temperature, and other internal factors. It is one of most important study in the field of engineering science, especially chemistry and mechanical engineering. In rigid body, the idealization of the solid body in which deformation is neglected. Deformation is known as the force acting on the solid state system which exerts change in its shape of the body but it continues to be at rest or in a uniform motion but it cannot accelerate. But those solid systems do have elasticity, compressibility and can be bent. This field is very vast since there are wide range of materials around us.
The study of mechanics of solids focus on rigid body, an appropriate material where the distance between any two particle remains fixed and difficult to separate them from each other. They are of static systems and dynamical system. In this study, the two most important factors is the stress-strain study. There at different advanced study where the solid system's deformation is located in the space like 2-D or 3-D.
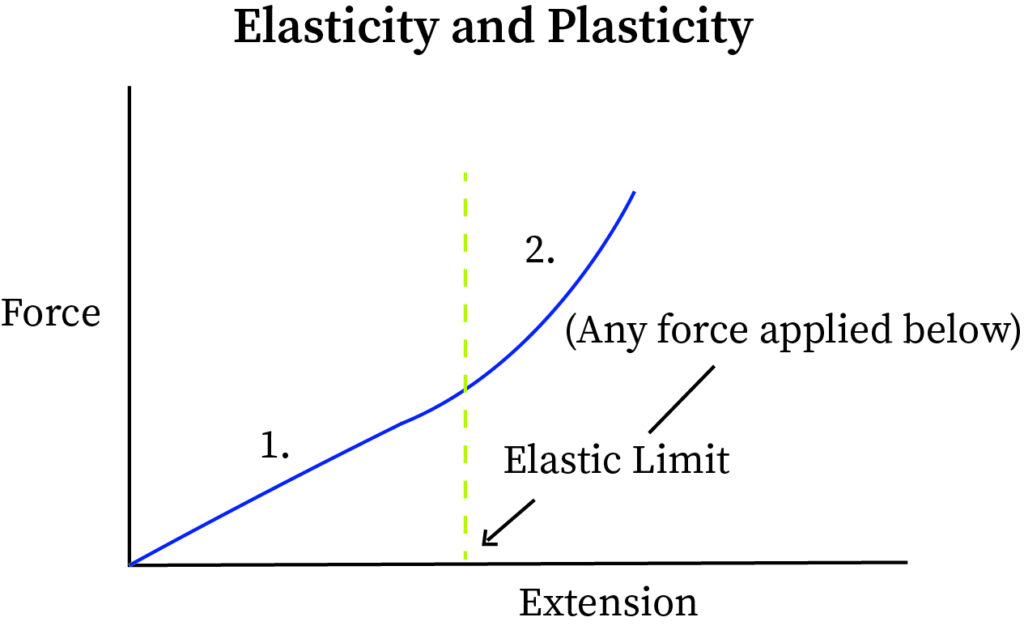
Elasticity vs Plasticity
The Elasticity property is defined as the property of a body which tends to regain its original size and shape when there is an external force removed and thereby causing deformation. For example like stretching a balloon or rubber band. There are different types like linear elasticity and non linear elasticity depending on the cross-section of the body. We study the stress and strain of the elastic solids, their problems, methods, constraints, theory, various mechanics and solutions for various materials in Solid mechanic engineering.
The plasticity property is defined as the property of a solid state body which have no force or tendency to regain its position back and cause permanent deformation. For example plastic spoon, mud.
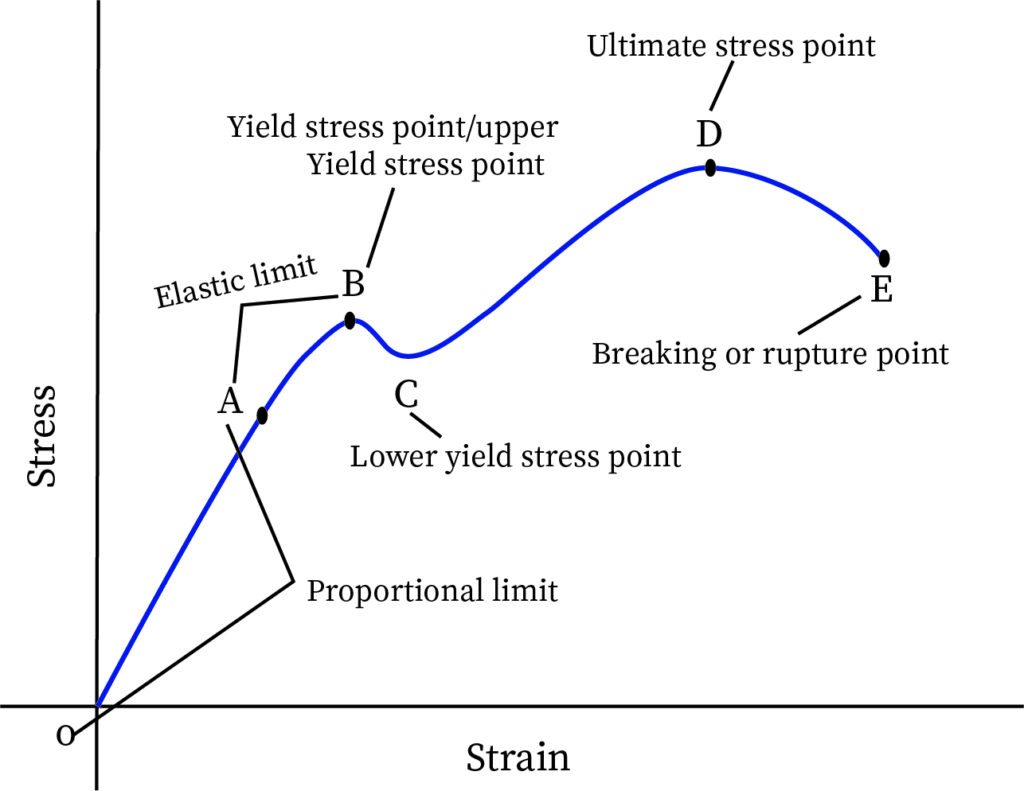
What is Stress and Strain?
Stress
Stress is the internal resistance exerted by the system to the external load applied per its unit cross sectional area. They are normal to the plane where they act and are tensile. As per the working of deformed solids, when an external force acts, the solids cause a deformation. So there is an internal force inside the solids which opposes this force due to the particles inside the solids where there is a strong coherent force between them and this force is called stress. So stress is restoring force per unit area developed inside the solid state system when deforming force acts. The SI unit of stress is Newton/metre2 or Pascal.
The equation of the stress is
σ=Force/Area.
There are two types of stress:
- Normal stress
- Tangential stress or shear stress
Normal stress : In the theory of solids, when stresses are normal to the area, then they are called normal stresses. It has two types, one is called the compressive stress when the solid has a decrease in its dimension due to the external force. It is also called uniaxial state of stress since the stresses act only in one direction. They are also called Bearing stress. The second type is tensile stress, i.e. when the solid has an increase in its dimension, that is the stresses are exerted when it is out of the area or into the area. Tensile strength's direction is always positive while the compressive stress is negative.
Shear stress of Tangential stress : For a solid system, if the cross sectional area is subjected to an external force which is tangential than normal, then the cross sectional area of the system is changed. So forces that are associated with the shearing of the material are called shear forces or shear strain, and the mechanical force that is needed to overcome this constraint is the shear stress.
A solid body like a metal bar hanging from a thin weightless rope hangs on its own weight and causes deformation due to its self weight. The principle of superposition of stress due to a number of loads acting on the solid is that the resulted stress is the stress caused by each of the load individually.
Strain
A strain of the solid system is defined as the ratio of the variation in the dimension to the original dimension of the solid system. When an external system of force acts on the body, a deformation is caused, the structure of the body gets disturbed and is termed as Strain.
It is mathematically denoted as,
Strain= Change in dimension or elongation/Original dimension
The strain is denoted as.
∈=δl/l.
Strain has no unit as it is a ratio.
There are three types of strain
- Longitudinal strain
- Shear strain
- Volumetric strain.
Longitudinal strain is defined as the ratio of the variation in length to the original length of a solid.
Shear strain is defined as the ratio of displacement of face to the height of the face where due to the tangential force the body gets distorted.
Volumetric strain is the ratio of the change in volume to the original volume of the solid state system.
Degree of Freedom of Solids
The degree of freedom is defined as the number of independent particles that is necessary to position an ideal rigid body in space, that is the number of direction the individual particles in a solid systems move. This study of degree of freedom include the study of kinematics of the solid system. There are various methods to calculate the degree of freedom depending on the dimension of the space, whether one, two or three dimension.
Hooks Law
This law in mechanics of solids states that for a small variation or change in the structure of the solid, the value of the stress and strain are proportional to each other. It is the empirical law where it defines the linear relationship of the elasticity of the rigid body. It is denoted as K or E where E is the Young's modulus or modulus of elasticity.
The young's modulus is defined as the ratio of stress and strain within the elastic range of the material.
Compressibility is the reciprocal of the modulus of the solid system which is denoted as 1/K
Poisson's Ratio
It is defined as the ratio of lateral strain to the longitudinal strain that is exerted due to the single stress on the body. It can also be the variation in length as per the length of the solid.
Advanced Mechanics of Solids
The meshless methods, continuum mechanics, meshless analysis, piezoelectricity of solids, the stress components of the solids, various constraints study like holonomic constraint, study of spatial mechanism, boundary value problem, heat transfer of various solids, basis functions and 2 D planar mechanisms comes under advanced mechanics.
Reference
One of the top books to refer for various problems and solutions for the advanced mechanics of solid is Advanced Mechanics of Solids by Otto T. Bruhns, 10th Edition is its updated version which has fundamental solutions for this concept. Also the AbeBook's Mechanics of the Solid state by Rimrott is also good.
Practice Problems
Q1) A metal wire of 1m long and of 2mm diameter is stretched by a load of 40kg. If the modulus of elasticity is 7×1010 N/m2 for the melt, find the stress, strain and force constant of the material of the wire.
Solution:
Convert the applied load into N.
Calculate the stress.
Calculate the strain.
Calculate the force constant.
Q2) What must be the elongation of the wire 5m long, to make the strain 1 % of 0.1 ? If the wire has cross-section of 1mm2 and is stretched by 10 kg-wt, what is the stress ?
Solution:
Calculate the elongation of the wire.
Convert the applied load into N.
Calculate the stress.
Q3) A wire is stretched by the application of a force of 50 kg wt/sq cm. What is the percentage increase in the length of the wire? The elasticity of the wire is 7×1010 N/m2 and the acceleration due to gravity is 9.8 m/s2 .
Solution:
Convert the applied load into N.
Calculate the percentage increase in length.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelors in Science (Physics)
- Masters in Science (Physics)
Want more help with your civil engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Mechanics of Solids Homework Questions from Fellow Students
Browse our recently answered Mechanics of Solids homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.