What is meant by the moment of a force?
In engineering mechanics, the moment of a force refers to the turning effect caused by an external force to a rigid body. A body is termed rigid if the relative position between any two arbitrary points on the body does not change when the body is under the influence of external force. In simple terms, a rigid body is un-deformable and has constant mass, and possesses definite inertia. A force normally causes a moment when the point of application of force lies eccentrically to the pivot point of the rigid body. Also, two equal and opposite force couples can cause moments. For example, a beam with both its ends free experiences a bending moment when acted by two equal and opposite concentrated moments at the two ends of the beam.
There are various practical applications of the concept of moments, like a rotation of the crank due to linear motion of the piston, the moment of inertia and its use in designing beams and columns, bending moment concept, torque, twisting moment, etc.
Here, in this article, a basic introduction has been provided regarding the concept of the moment.
Concept of the moment of a force
A force can cause a moment when the point of application of the force vector lies away at a certain distance from the point of pivot. The distance is generally known as a moment arm.
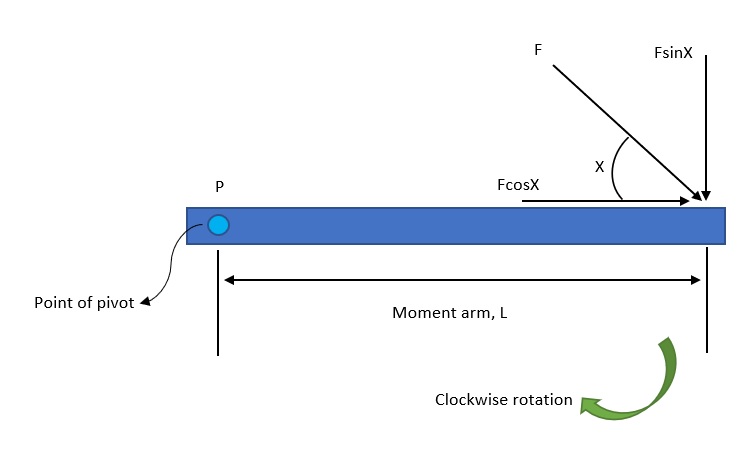
Consider figure 1 above, a rigid bar is pivoted at P and is acted by an external force acting at an angle . The distance from the point of application of force to the pivot point P forms a moment arm, . Resolving the force into its components along the two cartesian coordinates gives, and . The component is a distance of from the pivot point P forming a moment arm, while the component does not form any moment arm. Hence the force component cause a moment (clockwise rotation of the bar) about the pivot P. Mathematically, the expression of the moment is given by,
, where, denotes the moment of a force.
The effect is also known as torque. This concept is primarily used in wrenches, manual power jacks, and internal combustion engines that convert the linear reciprocating motion of the piston into rotary motion in the crankshaft.
Bending moment and twisting moment
Bending moment
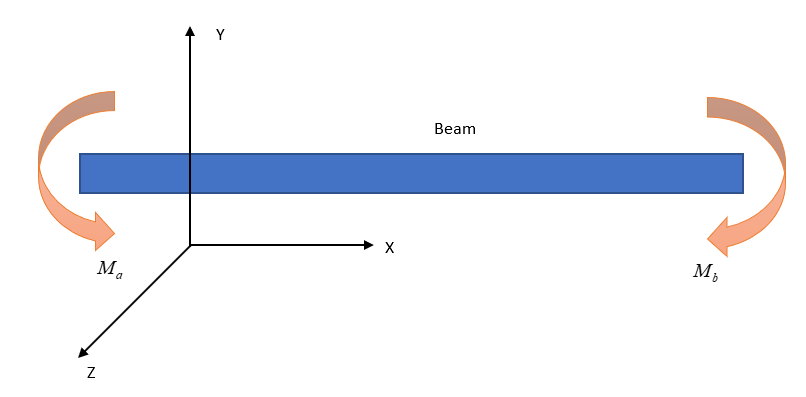
The concept of bending moment and twisting is extensively used in engineering mechanics and solid mechanics. Considering a solid circular beam (figure. 2) acted by two equal and opposite concentrated moments and at its two extreme ends about the Z-axis. These moments are such that they are parallel to the longitudinal axis of the beam, or perpendicular to the beam's cross-section. The moments will tend to bend the beam about the Z-axis. Bending moment is the internal resistance induced in the beam that tries to resist the bending that occurred. The amount of resistance is determined by the material property and cross-section of the beam (moment of inertia, ).
The general bending moment equation which can be used to determine the magnitude of bending moment and other relevant parameters is given by:
Where denotes the bending moment
denotes the bending stress
denotes the distance of fiber from the neutral axis
is Young's modulus of the beam
is the radius of curvature of the bent beam.
Twisting moment
The twisting moment is the resistance offered by a beam of the body when the external force moments tend to twist the beam. Considering the circular-cross sectional beam, the beam is acted by two equal and opposite force moments about the X-axis, or parallel to the beam's cross-section, or perpendicular to the longitudinal axis of the beam. The effect of the moment tends to twist the beam about the X-axis. The resistance to this twist is known as the twisting moment. The twisting moment of a beam is primarily a function of shear stress-induced, the torque applied, and the polar moment of inertia of the cross-section. Mathematically, the twisting moment equation of a beam is given by,
Where is the external torque applied
represents the polar moment of inertia of the beam's cross-section
represents the induced shear stress
R represents the radius of shaft
represents the shear modulus of beam
represents the angle of twist of beam
represents the length of the beam.
Moment of force and dynamics
Kinematics primarily deals with the motion of bodies without considering the forces or agents that caused the motion. But, in the area of dynamics, the motion of bodies, as well as the forces, are considered. For example, in many vibration problems, the moment caused due to a force and its consequent effect, such as simple harmonic motion is studied. A rod pivoted at one end and supported by spring on the other, undergoes simple harmonic motion if a force is applied at the spring side, which causes a moment at the pivot. The rotation of wheels due to torque applied causes the car to accelerate and achieve a terminal velocity, the torque applied by the driver to the steering wheels make the wheels turn, etc. are some examples where the moment of forces is studied under the branch of dynamics.
Context and Applications
The topic is extensively taught in different undergraduate and postgraduate degree courses of:
- Bachelors in Technology (Mechanical Engineering)
- Bachelors in Technology (Civil Engineering)
- Masters in Technology (Mechanical Engineering)
- Masters in Technology (Computation Mechanics)
- Masters in Technology (Machine Design)
Practice Problems
1. What is the necessary condition for a force to cause a moment?
- The force act eccentric to the pivot point.
- There should be a moment arm.
- Line of action of force should pass through the point of pivot.
- Both a and b
Answer: Option d
Explanation: To cause a moment, the external force should act at a point eccentric to the pivot point, and there should be a moment arm. These are two of the necessary conditions for a force to cause a moment.
2. What is meant by bending moment?
- The force which causes a bending in the beam.
- The force which makes the beam to undergo twisting.
- The resistance that a beam provides in response to a force that causes the beam to bend.
- Both a and c
Answer: Option d
Explanation: Bending moment is the resistance offered by a beam when an external force tries to bend the beam.
3. Twisting in a beam is a function of which of the following primary parameters?
- Torque
- Shear stress and torque
- Shear stress, torque, and polar moment of inertia
- Polar moment of inertia
Answer: Option c
Explanation: Twisting in a beam is the function of primary parameters such as shear stress, torque, and polar moment of inertia.
4. Which of the following is an example of dynamics related to moments?
- A circular disc spinning about a pivot center.
- Torque applied to a steering wheel that turns the wheels.
- Wrench tightening a nut.
- Both b and c.
Answer: Option d
Explanation: Torque applied to a steering wheel and a wrench tightening a nut both are examples of dynamics problems where the moment caused by an external force is taken into consideration along with the effect.
5. What is in twisting equation for a circular-cross sectional beam?
- Angle of twist
- Magnitude of external torque
- Magnitude of shear stress
- Magnitude of the radius of the beam
Answer: Option a
Explanation: The symbol represents the angle of twist of the beam when the beam is twisted by two equal and opposite external torque couples.
Want more help with your civil engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Moments Homework Questions from Fellow Students
Browse our recently answered Moments homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.