What is meant by plane stress?

Plane stress is a major area in the subject of continuum mechanics. Essentially, in continuum mechanics, the condition of the continuum is primarily followed. A matter is composed of a combination of atoms to form molecules, continuum mechanics assumes the distribution of the molecules to be uniform without any voids or spaces. The theory of elasticity is a complex area in terms of analysis, to account for simplicity, the majority of problems in elasticity can be treated as two-dimensional problems. This is also known as the plane theory of elasticity. Plane stress and plane strain are the two main areas where the plane theory of elasticity lays its emphasis.

As a general introduction, plane stress is a stress distribution in a three-dimensional body in space, essentially considering the stress components in a single plane, neglecting the third stress component in the other plane. The stress component in the other plane is considered to be zero. In this case, the stress tensor reduces to a $2\times 2$ square matrix instead of a $3\times 3$ matrix, with its elements directing towards two dimensions. This assumption greatly simplifies the analysis. The condition of plane stress occurs in the analysis of thin plates under external loads. For thin plates, the thickness of the plate is negligible as compared to its other two parameters. For analyzing slightly curved plates, the condition of plane stress can also be assumed, in such case, the third component of the stress is neglected. The condition of plane stress gives rise to plane strain, where the third component of strain is assumed to be zero. 

Stress tensor and Plane stress

For instance, consider the figure below (Fig. 1), An arbitrary body of area $A$ is considered. The body is under the influence of arbitrary external forces in the outward direction. The effect of the body is such that it tends to deform the body. Due to the body's material properties, the body tends to resist the deformation by inducing internal forces, known as stress. 

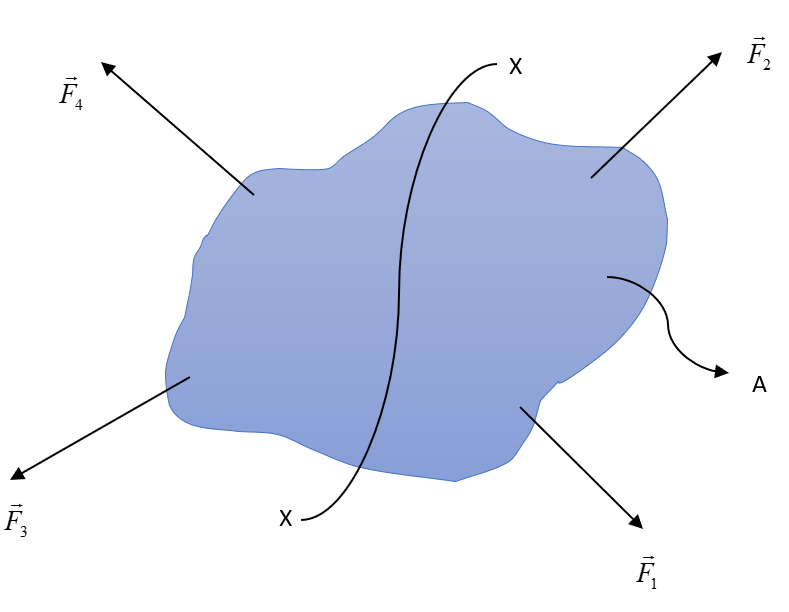
Splitting the body along the cross-section $X-X$ shows the internal force distribution. The internal force vectors are represented by ${\overrightarrow{F}}_i$. This is shown in the below-mentioned figure (Figure. 2).

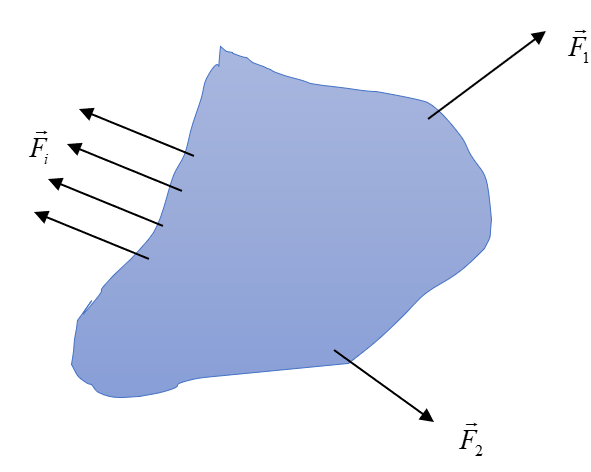
If a small infinitesimal area $dA$ is considered in the arbitrary body. The stresses can be better represented and resolved along the three dimensions. This is represented in the below-mentioned Fig. 3.

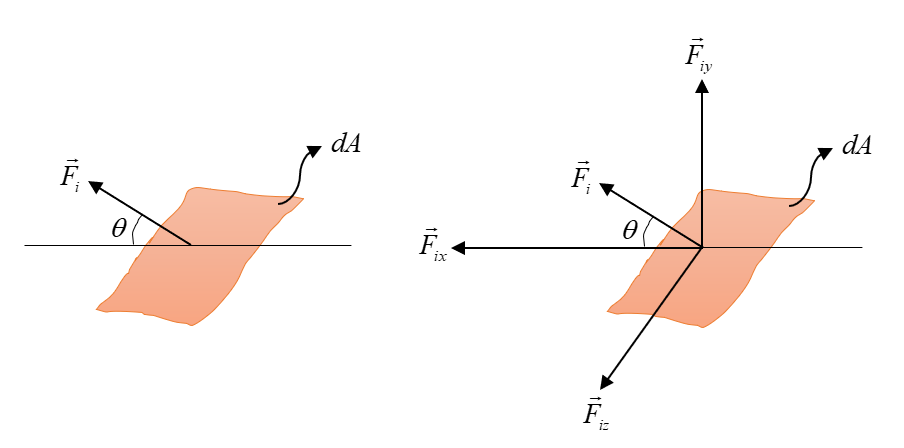
From elementary concepts, the stress acting on a body is simply the ratio between the force and the area where the force is acting. Then the internal force vectors, $\overrightarrow{F_{ix}}$, $\overrightarrow{F_{iy}}$, and ${\overrightarrow{F}}_{iz}$ will give rise to stress components along the $x,y$, and $z$-direction respectively. Out of which, $\overrightarrow{F_{iy}}$ will give rise to normal stress, and ${\overrightarrow{F}}_{ix}$ and $\overrightarrow{F_{iz}}$ will give rise to shear stresses. Shear stresses are those stress components that lie parallel to the cross-section of the area, as the force components along $x$ and $y$ are parallel to the area, hence the stresses are shear stresses. Similar to the internal force represented in Figure. 3, the body is acted by multiple internal force distributions, which gives rise to several normal and shear stresses. Hence, the stress tensor considering normal and shear stresses along three-dimension can be written as,

$\sigma =\left[\begin{array}{ccc}{\sigma }_x& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\sigma }_y& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\sigma }_z\end{array}\right]$ where ${\sigma }_x,{\sigma }_y$ and ${\sigma }_z$ represents the normal stresses along $x,y$, and $z$-direction respectively.

${\tau }_{xy}$ denotes shear stress at $x$ pointing along the $y$-direction

${\tau }_{xz}$ denotes shear stress at $x$ pointing along the $z$-direction

Similarly, ${\tau }_{yx},{\tau }_{yz},{\tau }_{zx}$ and ${\tau }_{zy}$ can be denoted.

The above stress state is three-dimensional. If the above stress state can be represented in a two-dimension form neglecting the stresses along the $z$-direction, it becomes a plane stress condition, which is given as,

$\sigma =\left[\begin{array}{cc}{\sigma }_x& {\tau }_{xy}\\ {\tau }_{yx}& {\sigma }_y\end{array}\right]$ where the symbols have their usual notations. This representation is termed as plane stress condition/representation. The condition of plane stress makes the stress analysis pretty simpler. 

Plane stress and Principal stresses

The plane stress analysis can be preferably done in two ways, they are, maximum shear stresses and principal stresses.

Analysis of plane stress using principal stresses

Considering an arbitrary cross-section under the influence of normal stresses along $x$ and $y$ directions. 

In the plane of the cross-section shown in Figure. 4, there are normal stresses as well as shear stress. If along the two planes the magnitude of shear stresses are zero and are under the influences of only normal stresses, those normal stresses are known as principal stresses and the corresponding planes are known as principal planes. Hence, with respect to the above figure, if ${\tau }_{xy}=0$, then ${\sigma }_x={\sigma }_1$ and ${\sigma }_y={\sigma }_2$ are the principal stresses. 

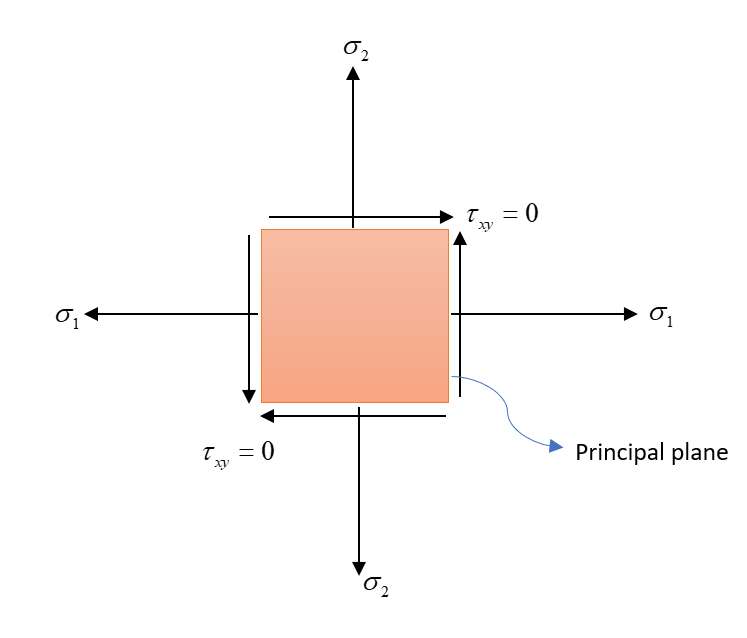
The location of the principal plane is given by the following relation,

$\tan 2\theta =\frac{2{\sigma }_x}{{\sigma }_x-{\sigma }_y}$, and the magnitudes of principal stresses, given the normal stresses, can be found out by using stress transformation equations. The stress transformation equations are given as,

$$\begin{gathered} {\sigma }_1=\frac{1}{2}\left({\sigma }_x+{\sigma }_y\right)+\sqrt{\frac{{\left({\sigma }_x-{\sigma }_y\right)}^2}{4}+{\tau }_{xy}^2} \\ {\sigma }_2=\frac{1}{2}\left({\sigma }_x+{\sigma }_y\right)-\sqrt{\frac{{\left({\sigma }_x-{\sigma }_y\right)}^2}{4}+{\tau }_{xy}^2} \end{gathered}$$

Analysis of plane stress using Maximum shear stress

The maximum shear stress is the shear stress where the magnitudes of shear stress reach the maximum at a particular orientation of the cross-section, the angle is given by $\theta$. It has been found that the magnitudes of shear stresses are maximum at an angle $\theta ={45}^0$. The maximum shear stress is given as,

${\tau }_{max}=\frac{1}{2}\left|{\sigma }_1-{\sigma }_2\right|$, where ${\tau }_{max}$ denotes maximum shear stress. These stresses are also known as in-plane stresses.  

Plane strain condition

The explanation for plane strain is similar to the plane stress condition. As stress-induced in the body gives rise to strain, plane stress condition gives rise to plane strain condition. Plane strain condition is a condition where the strain component along the perpendicular direction is considered to be zero, i.e. in a plane strain condition, the strain vector arises due to normal stress vector (along the $z$-direction) is zero. Similar to plane stress, the plane strain associated with an arbitrary cross-section can be denoted by the plane strain tensor, which is given as

$\epsilon =\left[\begin{array}{cc}{\epsilon }_x& {\vartheta }_{xy}\\ {\vartheta }_{yx}& {\epsilon }_y\end{array}\right]$ where ${\epsilon }_x$ and ${\epsilon }_y$ denote strain along $x$ and $y$ directions respectively

${\vartheta }_{xy}$ denotes shear strain at $x$ along the $y$-direction.

${\vartheta }_{yx}$ denotes shear strain at $y$ along the $x$-direction. 

One of the main applications of such a plane strain problem arises in the scenario of a long prismatic bar. Here the dimension of one of the parameters (length $z$) is very large as compared to the other two dimensions (breadth $x$ and width $y$). In such cases, if the bar is acted upon by external forces like shear force or axial force, they vary much along the $x$and $y$-axis of the body and not significantly along the $z$-axis. 

In civil engineering, the practical applications of such representation are used during the analysis of dams, tunnels, and different geotechnical analyses. 

Context and Applications

This topic is extensively taught in different undergraduate and postgraduate degree courses of:

• Bachelors in Technology (Mechanical Engineering)
• Bachelors in Technology (Civil Engineering)
• Masters in Technology (Mechanical Engineering)
• Masters in Technology (Civil Engineering)
• Masters in Technology (Machine Design)

Practice Problems

1. What is the other name of in-plane stresses?

1. Maximum shear stresses
2. Principal stresses
3. Normal stresses
4. Plane stresses

Answer: Option a

Explanation: Maximum shear stresses are known as in-plane stresses.

2. What is the condition for a stress tensor to be referred to as a plane stress condition?

1. ${\sigma }_x={\sigma }_y=0, {\sigma }_z\ne 0$
2. ${\sigma }_x={\sigma }_z=0, {\sigma }_y\ne 0$
3. ${\sigma }_x=0, {\sigma }_y={\sigma }_z\ne 0$
4. ${\sigma }_x={\sigma }_y\ne 0, {\sigma }_z=0$

Answer: Option d

Explanation: For a plane stress condition, ${\sigma }_x={\sigma }_y\ne 0, {\sigma }_z=0$

3. What is meant by thin plates?

1. The thickness of the plate is longer than its other two dimensions.
2. The thickness of the plate is negligible as compared to its other two dimensions.
3. The thickness of the plate is equal to its other two dimensions.
4. None of these

Answer: Option b

Explanation: For a body to be termed a plate, the thickness of the body should be negligible (very small) as compared to its other two dimensions. 

4. Which of the following is true regarding a plane strain?

1. In a plane strain, the perpendicular strain associated with a body is considered to be zero.
2. In a plane strain, the $x$and $y$ components of strain are zero.
3. In a plane strain, only the $x$ component is zero, while the $y$ component is non-zero.
4. In a plane strain, all components of the shear strain are zero.

Answer: Option a

Explanation: In the plane strain condition, the perpendicular strain, i.e. the perpendicular component of strain is considered to be zero. 

5. Which of the following is the correct plane stress tensor?

1. $\left[\begin{array}{cc}{\sigma }_x& {\tau }_{xy}\\ {\tau }_{xy}& {\sigma }_y\end{array}\right]$
2. $\left[\begin{array}{cc}{\sigma }_y& {\tau }_{yz}\\ {\tau }_{yz}& {\sigma }_z\end{array}\right]$
3. $\left[\begin{array}{cc}{\sigma }_z& {\tau }_{zx}\\ {\tau }_{zx}& {\sigma }_x\end{array}\right]$
4. None of these

Answer: Option a

Explanation: The correct plane stress condition is represented by $\left[\begin{array}{cc}{\sigma }_x& {\tau }_{xy}\\ {\tau }_{xy}& {\sigma }_y\end{array}\right]$.