What is meant by volume?
Volume usually is the dimensional quantity that involves the evaluation of any three-dimensional figure enfolded inside a closed space. The SI unit (International System of Units) of volume is m3 and the dimensional unit of volume is [L3]. For estimation of the volume of any figure, various formulae are used. Another application of volume includes the reference in the sound levels, the higher the sound intensity, the louder the sound heard, and hence, the larger the volume. The SI unit of sound volume is decibels (dB).
| Geometric figures | Volume equation | Annotation |
Cube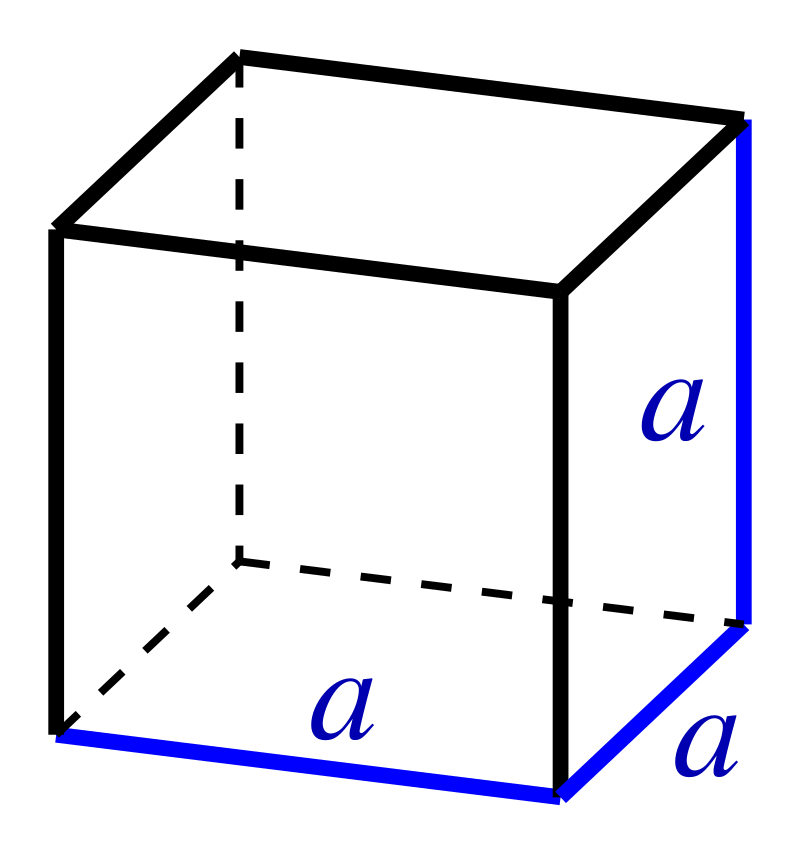 CC BY-SA 4.0 | https://commons.wikimedia.org | Ag2gaeh | V = a3 | a = edge or side length |
Cuboid CC BY-SA 4.0 | https://en.wikipedia.org | Quader | V = a x b x c | a = length, b = width and c = height |
Cylinder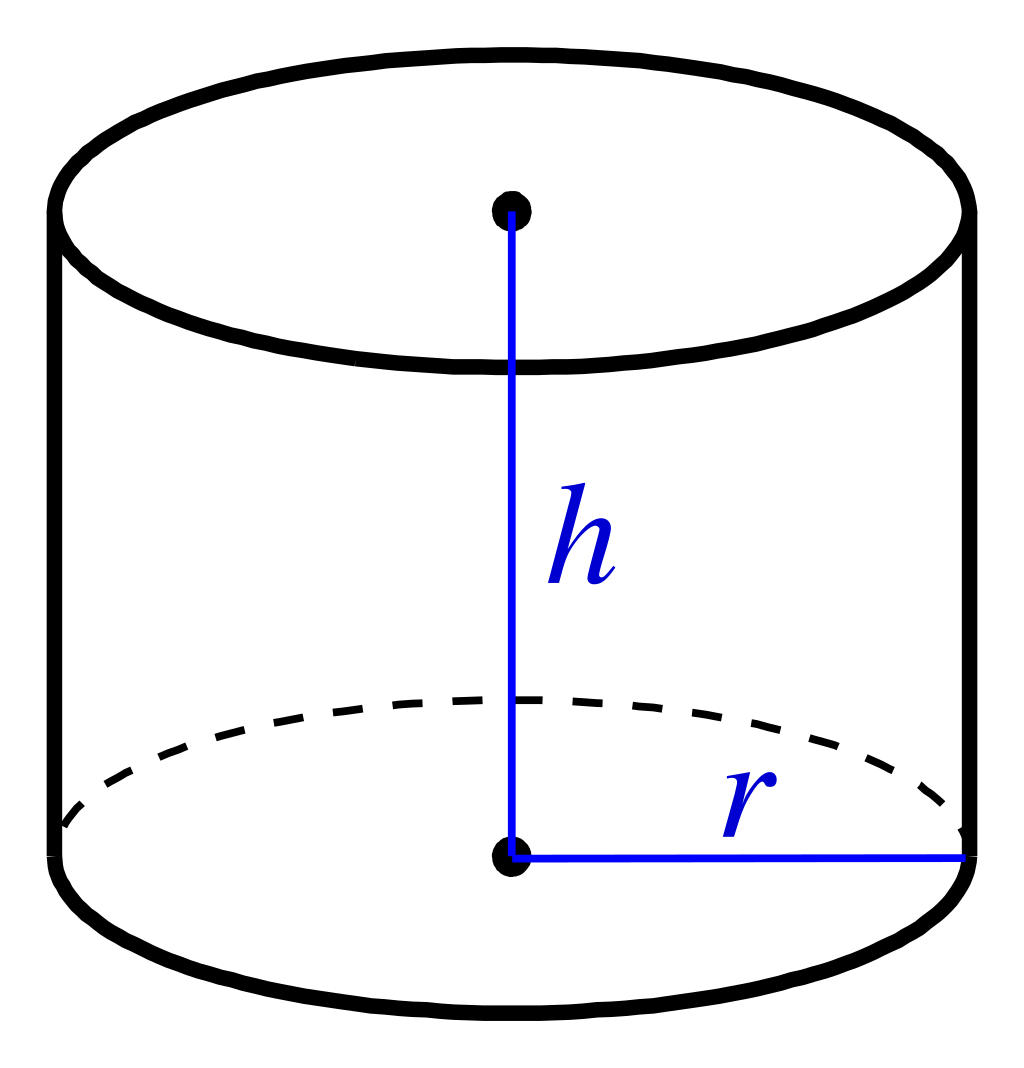 CC BY-SA 4.0 | https://en.wikipedia.org | Ag2gaeh | V = πr2h | r = radius of the base and h = height |
Prism CC BY-SA 4.0 | https://en.wikipedia.org | Ag2gaeh | V = B x h | B = base area (s2 for square and length x breadth for rectangle) h = height of the prism |
Sphere CC BY-SA 4.0 | https://en.wikipedia.org | Ag2gaeh | V = (4/3) πr3 | r = radius of sphere |
Cone CC BY-SA 4.0 | https://en.wikipedia.org | Ag2gaeh | V = (1/3) x πr2h | r = radius of base h = height of the cone |
Ellipsoid CC BY-SA 4.0 | https://en.wikipedia.org | Ag2gaeh | V = (4/3) x π x a x b x c | a, b, c = semi-axes of an ellipsoid |
Pyramid CC BY-SA 4.0 | https://en.wikipedia.org | Ag2gaeh | V = (1/3) x B x h | B = base area (s2 for square and length x breadth for rectangle) h = height (base to peak) |
Tetrahedron CC BY-SA 4.0 | https://en.wikipedia.org | Ag2gaeh | V = (a3/6√2) | a = edge or side length |
Computation of volumes
In civil engineering, volume calculations are crucial in surveying and geotechnical fields. For instance, earthwork calculations near roads, rails, sewage systems, determining the capacity of reservoirs, and so on.
There are three methods present for the computation of volumes:
- Cross-sectional volume computation
- Spot levels volume computation
- Contours volume computation
The cross-sectional volume computation is used for computing the earthwork of roads, canals, rails, or sewage systems. The spot levels volume computation is useful for determining earthwork in the foundations of high-rise buildings and the contours volume computation is utilized for evaluating the capacity of reservoirs.
Computation of volume from cross-sections
Profile leveling is the first step to be carried out for calculating earthwork along the central alignment line of the object and the cross-sectional levels are recorded at regular distances.
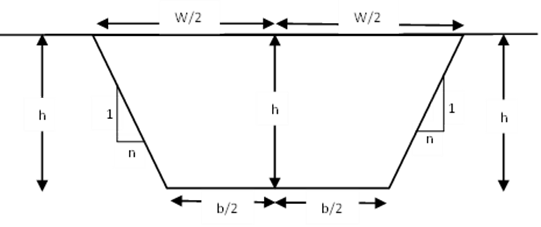
If the section is levelled, the cross-sectional area is calculated as below.
Let ‘h’ be the depth at the central alignment line and 1: n be the side slopes. Thus,
w = b + 2nh
Area = 1 /2 (w + b) h=1 / 2 (b + 2nh + b) h
∴ Area = (b + nh) h
If the section is multilevel, the cross-sectional area is calculated by:
Area of the figure = 1 /2 [ Σ Product of pair of coordinates joined by continuous lines – Σ Product of coordinates joined by dotted lines]
Once the cross-sectional area at different sections is computed, determine the volume by the either trapezoidal or prismoidal method.
Trapezoidal Method
where 'n' is the number of segments at an interval of 'd' and area at L = nd as .
Prismoidal Method
Computation of earthwork from spot levels
This method is used to obtain the volume of earthwork for the elevation of certain basements, huge tanks, and to borrow pits. In this method, the entire area is separated into several rectangles or triangles. The levels are taken at the corner points before and after excavation as well. The depth of excavation at each corner point is noted down and then for each simple figure (rectangle or triangle), the depth is measured.
Volume = Area of the figure x average depth
Thus, for a rectangle with corner depth ha, hb, hc, and hd
Volume = Area of rectangle x (ha + hb + hc + hd / 4)
and for a triangle,
Volume = Area of triangle x (ha + hb + hc / 4)
Thus, from the entire figure, all the separate volumes of triangles and rectangles are added together for the total volume of work.
Computation of volume from contours
The capacity of the reservoir is equivalent to finding the volume of water, filled inside the reservoir. The entire area resting inside the contour line is determined by a planimeter. Make sure that the area which is to be measured is not situated between two consecutive contour lines. The volume can be found out by using the trapezoidal rule and prismoidal rule by substituting the respective values in the equations.
Context and Applications
- Bachelors in Technology (Civil Engineering)
- Masters in Science (Surveying and GIS)
- Masters in Commerce (Statistics and Economics)
- Masters in Technology (Geotechnical Engineering)
Practice Problems
1. What are the SI unit and dimensional unit of volume?
- m4 and [L4]
- m3 and [L3]
- m2 and [L2]
- m and [L]
Correct option- b
Explanation: The SI and dimensional units of volume are m3 and [L3].
2. Which shape represents the formula of volume = πr2H?
- Cylinder
- Triangular pyramid
- Square or rectangular pyramid
- Ellipsoid
Correct option- a
Explanation: The cylinder shape represents the formula of volume = πr2H.
3. Which volume computation method is useful for determining earthwork in the foundations of high-rise buildings?
- Cross-sectional volume computation
- Contours volume computation
- Spot levels volume computation
- Trapezoidal and prismoidal method
Correct option- c
Explanation: The spot levels volume computation method is useful for determining earthwork in the foundations of high-rise buildings.
4. What is the SI unit of sound volume?
- Ampere (A)
- Newton (N)
- Joule (J)
- Decibel (dB)
Correct option- d
Explanation: The SI unit of sound volume is the decibel (dB).
5. Which of the following statement(s) is/are incorrect?
- Once the cross-sectional area at different sections is obtained, we can determine the volume by either the trapezoidal or prismoidal method.
- In civil engineering, volume calculations are crucial in surveying and geotechnical fields.
- Profile leveling is the penultimate step to be carried out for calculating earthwork along the central alignment line of the object and the cross-sectional levels are recorded at regular distances.
- The capacity of the reservoir is equivalent to finding the volume of water, filled inside the reservoir. The entire area resting inside the contour line is determined by a planimeter.
Correct option- c
Explanation: Profile leveling is the first step to be carried out for calculating earthwork along the central alignment line of the object and the cross-sectional levels are recorded at regular distances.
Related Concepts
- Volume computation of dams
- Cylindrical container volume
- Perimeter and volume of figures
- Offset method in surveying
Want more help with your civil engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Volumes Homework Questions from Fellow Students
Browse our recently answered Volumes homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.