What is summation?
In mathematics, the summation is the process of adding a sequence of numeric values, known as addends and their result is called sum or total. The term summation refers to the addition or sum of two or more numbers or units. For example-
Sum = 1+2+3+4+5
This is the sum of digits from 1 to 5 in a sequence. The total of these numbers is 15. This is a straightforward computation. In the above calculation, the numbers or sequences can be written one after the other using the plus (+) symbol (addition symbol), such as 1+2+3+4+5. However, it is difficult to write all the elements when the sequence of numbers is quite long and the summation has numerous terms.
To avoid this, a summation symbol was devised in mathematics. This summation symbol is a large, uppercase, Greek letter sigma ∑ . The notation is described in the figure below.
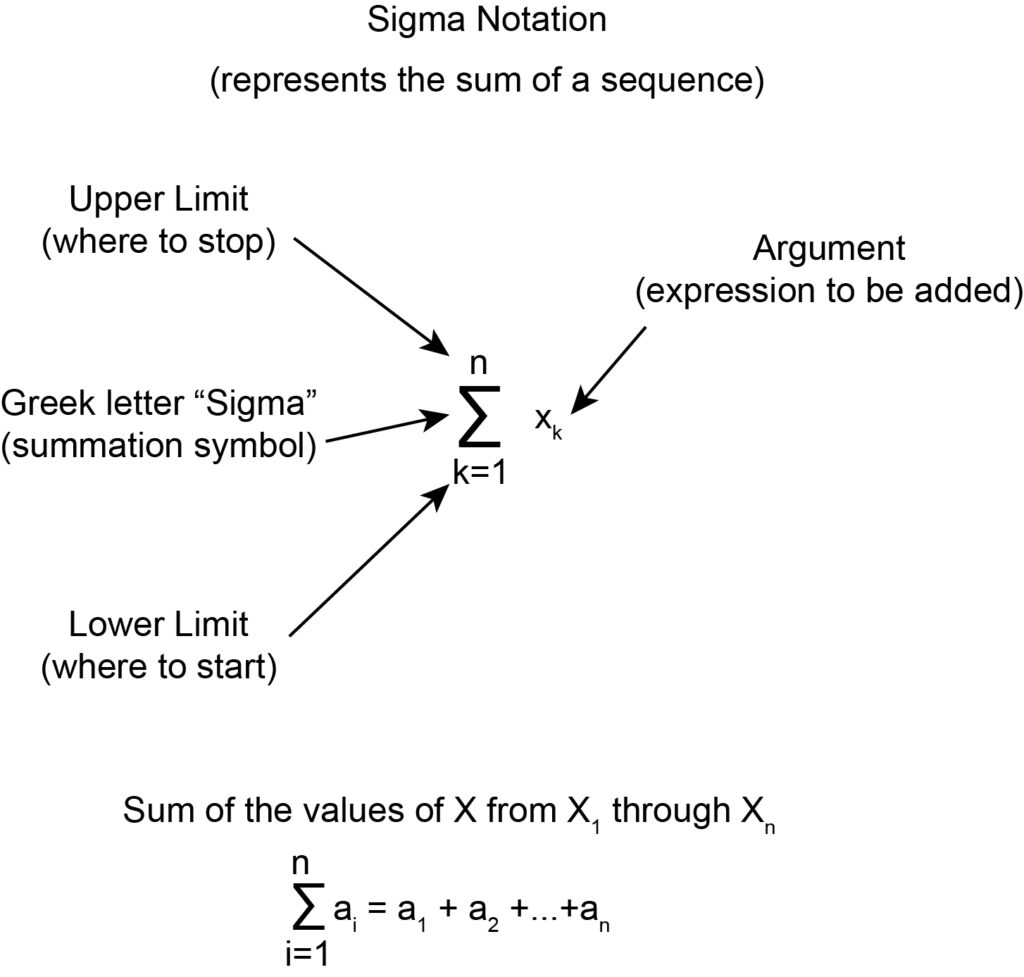
An example of summation notation is -
Here, is the lower bound of the summation. It is the initial or starting number or first term of the sequence. is the upper bound of summation which is the end limit of summation and (argument) indicates the sequence of numbers like 1,2,3,4----100. The value of is always an integer number and it increases by 1 for each succeeding term.
Suppose that if the summation has no limit which means the summation has no upper bound. Then the summation goes to the infinite limit such that the summation starts from to unlimited value of , that is 1+2+3+4+5+----------------, which is denoted as follows:
In this notation, the infinity symbol is used. The symbol is known as infinite. The upper bound shows that continue to increase without limit. So, it is the summation of to infinity.
Summation function
The summation is used to examine the continuity of addition. Suppose is a function. The summation of a function from to where is the lower bound and upper bound of summation respectively. An example of a summation function is:
Here is the summation function. The result of this function 9. This function is bounded from 1 to 3.
If summation has an infinite sequence, then it is called a series. The summation is of two types- divergent summation and convergent summation. If the summation is not bounded by any digit or a fixed number then it is called divergent summation because the sum expands without the limit. If summation is bounded with limits or numbers then it is called convergent summation.
Bounded summation
There are a variety of ways for bounding the summations that define algorithm execution times. Here are a few of the most popular approaches. The bounded summation satisfies many theorems.
Mathematical induction of bounded summation
Mathematical induction is the most basic method for evaluating a series For example- The arithmetic series evaluates to . If we put , we can easily verify this series. As a result, we make the inductive assumption that it holds for n and prove it for . We have got:
So, it is true for . To apply mathematical induction, one does not need to guess the exact value of a summation. Induction can also be used to demonstrate a bound. For another example the let us prove that geometric series is . Prove for some constant c. if we put , then as long as . Let us assume that the bound holds for and then show that it also holds for . We have got:
The value of or so , as we wanted to prove. This is the concept of bounded summation.
When using asymptotic notation to prove boundaries via induction, we must be cautious. Take a look at the following fallacious proof, that . Certainly, . Assuming the bound for , we now prove it for :
<= wrong!!!
The error in the argument is that the "constant" concealed by the "big-oh" expands with n and is hence not constant. We have not demonstrated that the same constant applies to all n.
Use of integration for the Summation
The integration is defined as the summation of values. A definite integral has a limit whereas the indefinite integral works similar to unbounded summation. See the figure below. The area is bounded by the x-axis and a and b are the limits of the area. The curve function is .


There are numerous methods for estimating this area. Assume we divide the area into thin vertical stripes, similar to the one illustrated, and each strip is roughly rectangular. The area under the curve is then approximated by adding the areas of the rectangular strips.
From the point P, a standard strip is drawn . The width of the strip is indicated by the letter . The sign is used to represent a modest rise in the variable being analyzed, in this case, x. The strip's height is equal to the curve's value at point P, which is. As a result, the area of the strip illustrated is roughly . Assume that the area of this little strip is equal . Because this strip contributes a minor amount , to the total area , under the curve, we employ the delta notation once more. Then
We may calculate the entire area under the curve by adding the areas of all such thin strips from to , which we represent by .
To improve the accuracy of this approximation, we must reduce the thickness of each strip to a very small value, i.e. we let , giving
This is referred to as a sum's limit. If there is a limit, we will write it as. As a result, a definite integral is defined as the limit of a sum. As a result, we get the significant result that
Therefore, integration might be thought of as a process of adding up or summarizing.
Concepts and Applications
This topic is significant in the professional exams for both graduate and postgraduate courses, especially for:
- Bachelor of Technology in Computer Science
- Master of Technology in Computer Science
Related Concepts
- Summation notation
- Summation algorithm
- Convergence summation
- Divergence summation
Practice Problems
Q1. What is the symbol of summation-
Correct answer- 2.
Explanation- is the symbol of addition used to add a large sequence.
Q2. What is the value of if i = 0.
- 10
- 10+n
- n+10
- 0
Correct answer- 1. 10
Explanation- If i = 0,
Q3. If the summation is not bound by any limit then this is known as:
- Convergent
- Divergent
- None
- Infinite
Correct answer- 2. Divergent
Explanation- A divergent series is an infinite series that is not convergent, which means that the infinite sequence of partial sums of the series has no finite limit in mathematics.
Q4. The value of finite series is always:
- non-defined
- well-defined
- none
- integral
Correct answer- 2. well-defined
Explanation- "Well-defined" means that the total exists and equals the same real number regardless of the sequence in which the terms are added.
Q5. Which statement is false:
- A Cauchy sequence of real numbers need not be bounded.
- A sequence of real numbers need not be bounded.
- A sequence of real numbers is convergent if and only if it is a Cauchy sequence.
- The series is convergent.
Correct answer- 1. A Cauchy sequence of real numbers need not be bounded.
Explanation- Every Cauchy sequence of real numbers has a convergent subsequence, and so is itself convergent, according to Bolzano–Weierstrass. The least upper bound axiom is implicitly used in this demonstration of the completeness of the real numbers.
Want more help with your computer science homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Bounded Summation Homework Questions from Fellow Students
Browse our recently answered Bounded Summation homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.