What is Longest Common Subsequence (LCS)?
The Longest Common Subsequence (LCS) is defined as the longest subsequence that is shared by all of the given sequences, assuming that the subsequence's elements do not have to be in consecutive locations in the original sequences. It is used in the areas like bioinformatic, revision control systems like SVN and Git.
Example 1:
Input: text1 = " WXYZ ", text2 = " WYXWZ "
Output: 3
Consider the sequences (WXYZ) and (WYXWZ), having 5 common subsequences of length 2 (WX), (WY), (WZ), (XZ), and (YZ); 2 subsequences of length 3: (WXZ) and (WYZ). There are no subsequences common other than these 7. So (WXZ) and (WYZ) are their longest common subsequences.
Example 2:
Input: text1 = "acbee", text2 = "adce"
Output: 3
Explanation: The longest common subsequence in the given string is "ace" is having length 3.
A subsequence, also known as a pattern or a new string created from input string that contains some or no characters and can be obtained without altering the order of the characters. Subsequences unlike substrings, are not necessary to be at adjacent places within the original string.
How to find Longest Common Subsequence?
Most commonly used techniques used to find LCS of the given strings are listed below.
- Dynamic programming
- Backtracking
Dynamic Programming
The computation of their longest common subsequence, or LCS, is a typical problem that can be solved in O(nm) time with dynamic programming.
- Let's start by defining the function lcs() to return the length of the longest common subsequence of the strings P and Q.
- Let the length of P and Q is n and m respectively. As a result, the goal is to find lcs(n,m).
- For defining lcs(i,j), we have to consider the following 2 possibilities:
- If Pi==Qj , then the last letter of the longest common subsequence is Pi. And the remaining letters of both strings should be checked for common letters. So in this case, the function can be defined as lcs(i,j)=1+lcs(i-1,j-1).
- If Pi≠Qj, then only one of these letters will be the last letter of LCS. So the function should be defined considering both as part of LCS. If Pi is considered to be part of LCS, then the letters up to Pi and Qj-1 should be matched. If Qj is considered to be part of LCS, then the letters up to Pi-1 and Qj should be matched. So the function can be defined as lcs(i,j)=max(lcs(i,j-1),lcs(i-1,j)).
The pseudocode for the above given algorithm can be written as follows:
function
Dynamic Programming-Example
Consider the strings
P: aabbcc
Q: abcc
Here . So the function called will be .
- First the function will check if the index values are 0. Here it is not.
- Then it will check if the last letters match. Here , so the result returned is 1+ recursive call. That is .
- The recursive call to the function also checks for the last letters. As it is a match, the result returned will be: .
- On recursive call , the last letters matches. and the result returned is .
- On call , the last letters of substrings and , does not match. So the second case will be considered. Now, the result returned will be: .
- The recursive call will return 0, as one index value is 0. The call will return , as there is a match of letters in substrings and .
- The recursive call will return 0, as second value is 0.
- So the result of is: 1(from step 2)+1(from step 3)+1(from step 4)+1(from step 6)=4.
- The longest common subsequence of and is of length 4. From the strings, it can be identified that the string is .
Backtracking Algorithm
Backtracking algorithm uses a brute-force approach to find the optimal solution.
The name signifies that if the current solution is not optimal or suitable, then go back to previous step and find another solution.
Backtrack algorithm approach is used to solve problems that are having many solutions. If one wants optimal solution, then they can use dynamic programming. State space tree is a tree which represents all possible combination of states of the problem. It includes solutions and non-solutions combination.
Backtrack algorithm is given below:
Consider two strings and . The state space tree for the problem of finding LCS is given below:
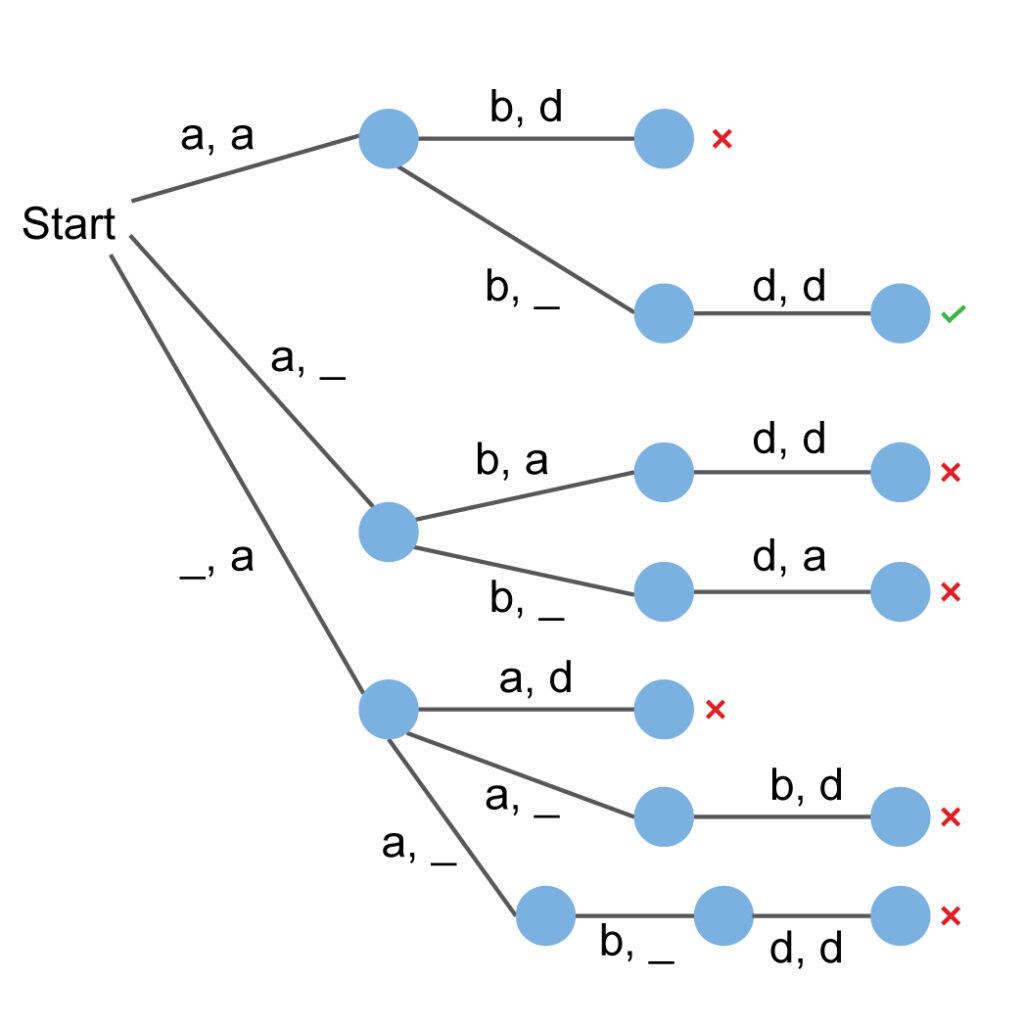
The state space tree shows the possible matching of the letters of both strings. Here, the parser will perform a top-down traversal on matching the possible combinations of the letters. When it finds the longest matched string, it will be considered as the final solution.
Comparison between Dynamic Programming and Backtracking
Dynamic programming divides the complex problem into simpler problems and solves it, by reusing solution for similar sub problems whereas backtracking is a recursive technique, in which all the possible solutions are generated and the infeasible solutions are eliminated. The number of function calls is reduced using the dynamic programming approach. It saves the outcome of each function call so that it can be reused in subsequent calls, avoiding unnecessary calls. As a result, the time it takes a dynamic method to fill the table precisely is same as the time it takes to fill the table (i.e. O(mn)). The backtracking algorithm, on the other hand, is more difficult. The main difference is that dynamic programming provides the optimum solution, whereas backtracking considers all possible solutions for the problem.
Complexity
The problem is NP-hard, for most of the general case of arbitrary input count. The problem is polynomial time solvable by using dynamic programming approach, when the number of input sequences is constant.
- For strings of lengths p and q, the running time of the dynamic programming algorithm is O(p × q), whereas, the Backtracking algorithm has the complexity of 2max(p, q)
- Backtracking method needs exponential time, as it needs to check every combination of the strings.
- There also exist approches with lower complexity, that also depends on the size, that is the input length, the length of the LCS, or both.
Application of Longest Common Subsequence (LCS)
- Used in linguistics and bioinformatics.
- Used by revision control systems like Git for confirming changes made to a revision-controlled collection of files.
- Common sequence identification is also used in biometrics.
Common Mistakes
There is a chance of misunderstanding that LCS should be present in consecutive place of letters in original strings. But it is wrong, the subsequence can have any place, but the sequential order should be preserved. Out of the many algorithms that are available to solve LCS problem, the most efficient runtime complexity considered for it is O(m*n). But there are many ways to speed up the running time of the problem, this can be done by creating a reverse index (string to location HashMap) for one of the two strings. Although this method is not effective with short strings as creating the map takes time, but is useful for strings having several hundred characters.
Related Topics
- Longest increasing subsequence
- Longest alternating subsequence
- Dynamic Programming
- Recursive Programming
Context and Applications
This topic is significant in the professional exams for both graduate and postgraduate courses, especially for:
- Bachelors in Computer Science
- Masters in Computer Science
- Bachelors in Computer Application
- Masters in Computer Application
Practice Problems
Q1. Time Complexity for Dynamic Programming is
a) O(n log n)
b) O(mn)
c) O(m+n)
d) O(n)
Correct Answer- b) O(mn)
Explanation: As the dynamic method should go through both of the strings, the complexity is based on length of both strings.
Q2. Longest common subsequence is an example of ___________
a) Greedy Algorithm
b) Divide and Conquer
c) 2D dynamic programming
d) 1D dynamic programming
Correct Answer- c) 2D dynamic programming
Explanation: The presence of substring can be marked by using a table data structure by considering all possible combination of strings. So it is 2 dimensional.
Q3.Which of the following problems can be solved using the longest subsequence problem?
a) Longest bitonic subsequence
b)Longest increasing subsequence
c) Longest palindromic subsequence
d) Longest decreasing subsequence
Correct Answer- c) Longest palindromic subsequence
Explanation: The additional checking is needed for the sequence is palindrome or not.
Q4. Longest common subsequence problem can be solved by using which method?
a) Recursion
b) Both recursion and dynamic programming
c) Greedy algorithm
d) Dynamic programming
Correct Answer- b) Both recursion and dynamic programming
Explanation: The LCS problem can be solved by both methods, although the dynamic method is the best solution.
Q5. Which algorithm is generally faster than dynamic algorithm?
a) Greedy Algorithm
b) Naïve Algorithm
c) Recursive Algorithm
d) Backtracking Algorithm
Correct Answer- a) Greedy Algorithm
Explanation: It is an approach for solving a problem by selecting the best available option.
Want more help with your computer science homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Longest Common Subsequence Homework Questions from Fellow Students
Browse our recently answered Longest Common Subsequence homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.