What is merge sort?
Merge Sort recursively sorts a given collection of numbers or elements by using the divide and conquer strategy in less time. It is one of the most used algorithms, with the worst-case time complexity of O (n log n). It was invented by John Von Neumann. The algorithm continuously divides an array into sub-arrays until each sub-array consists of a single element. It then merges those sub-arrays to produce a sorted array.
Divide and conquer strategy
In the divide-and-conquer approach, a large problem is divided into smaller subproblems. Each subproblem is further divided into subproblems until it becomes simpler to solve the subproblems directly. After finding the solution to each subproblem, the solution of all subproblems is integrated to give the solution to the original (large) problem.
The divide-and-conquer strategy consists of the following three stages:
- First, divide the problem into smaller problems.
- After that, solve the sub-problems to conquer them. The aim is to break down the original problem into atomic sub-problems such that they can be solved easily.
- Finally, to find the answer to the main problem, combine the solutions of the sub-problems.
Working of merge sort
When the merge sort algorithm is used to sort an unsorted array, it will work as follows:
- Merge sort will divide the unsorted array into two halves.
- It will continue dividing each sub-array until a single element is left in the array.
- Then, the merge sort algorithm will arrange the sub-arrays to create a sorted array.
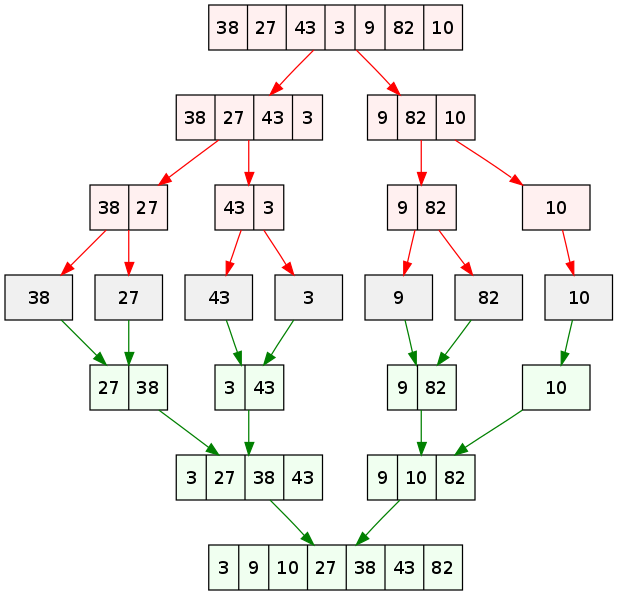
For example, if the original array contains six elements, the merge sort algorithm divides it into two subarrays of three elements each. However, these sub-arrays will require further sorting. Hence, each of them will be divided into two parts again, and the same process will continue until a single element is left in the array. Then, the sorted subarrays will be merged to create a single sorted array.
Consider an array containing the following values: int arr {38,27,43,3,9,82,10}
A visual depiction of how the merge sort algorithm sorts the provided array is given below:
Algorithm of merge sort
- Create a variable called p and store the first index/ first element of the array in it. Pick another variable, r, and store the array's last index in it.
- Then, use the formula (p , to identify the middle element. Mark the index of the middle element as q.
- Then divide the array into two sub-arrays, from p to q and from to r index.
- Divide these two sub-arrays again, recursively.
- Begin merging the sub-arrays after the main array is separated into sub-arrays with single items.
- Compare the first element of the first subarray with the first element of the second subarray. If the element of the first subarray is smaller, then add it to the merged list. Move to the next element in the first subarray. Otherwise, add the element from the second subarray and move to the next element. The process is repeated till one of the lists is empty. The remaining elements of the non-empty list are added to the merged list.
- The same process is repeated till all the subarrays are merged into a single array. The final array represents the sorted list.
Implementing merge sort algorithm
C program implementing the merge sort algorithm is shown below.
#include <stdio.h>
void merge(int a[], int j, int q, int r)
{
int b[7]; //same size of a[]
int i, j, k;
k = 0;
i = p;
j = q + 1;
while(i <= q && j <= r)
{
if(a[i] < a[j])
{
b[k++] = a[i++]; // same as b[k]=a[i]; k++; i++;
}
else
{
b[k++] = a[j++];
}
}
while(i <= q)
{
b[k++] = a[i++];
}
while(j <= r)
{
b[k++] = a[j++];
}
for(i=r; i >= p; i--)
{
a[i] = b[--k]; // copying back the sorted list to a[]
}
}
void mergeSort(int a[], int j, int r)
{
int q;
if(p < r)
{
q = (p + r) / 2;
mergeSort(a, p, q);
mergeSort(a, q+1, r);
merge(a, p, q, r);
}
}
void printArray(int a[], int size)
{
int i;
for (i=0; i < size; i++)
{
printf("%d ", a[i]);
}
printf("n");
}
int main()
{
int arr[] = {38,27,43,3,9,82,10};
int len = sizeof(arr)/sizeof(arr[0]);
printf("Given array: n");
printArray(arr, len);
mergeSort(arr, 0, len - 1);
printf("nSorted array: n");
printArray(arr, len);
return 0;
}
output:
Given array:
38 27 43 3 9 82 10
Sorted array:
3 9 10 27 38 43 82
Time and space complexity analysis of merge sort algorithm
- Merge sort follows the divide-and-conquer approach. So, the algorithm divides the number of elements (array) in half at each step. This step can be denoted using a logarithmic function, log n. The total number of steps will be given as .
- Additionally, a single-step operation is carried out to determine the middle element of the subarray. This operation takes O(1) time.
- To merge the subarrays, the algorithm takes O(n) time.
- Consequently, the total time taken by the merge sort algorithm will be , which means the time complexity of the algorithm will be .
In-depth analysis
Consider the following to understand the merge sort time complexity analysis more clearly:
- The divide part of merge sort takes O(1) time, as mentioned above.
- The conquering part solves two subproblems of n/2 size recursively. It takes T(n/2) time for each subproblem. The final time complexity of the conquer part is 2T(n/2).
- Assume that the combination part takes the worst-case time complexity O(n).
- Now, to find T(n), all the complexities should be added.
Now, by solving the above recurrence relation using Master’s Theorem,
Where, a = 2 and b = 2
Therefore, k = 1
Also,
Now, according to the 2nd case of master’s theorem:
If
The merge sort recurrence relation satisfies this condition of Master’s theorem. Hence, the time complexity of merge sort is .
Further, the space complexity for merge sort is O(n).
Merge sort in linked lists
Like arrays, merge sort can also be applied to sort linked lists. The process of sorting a linked list is similar to that of sorting arrays. The list is first divided into two equal parts to create sub-lists. Later, the sub-lists are again divided to obtain sub-lists, and the same procedure is continued till a single element is left in the linked list. When the sub-lists are left with a single element, they are recursively merged to obtain a sorted linked list.
Context and Applications
The subject is important in high school, undergraduate, graduate level, and all the entrance exams relating to computer science or information technology field, particularly for:
- Bachelors in Network Communication
- Bachelors in Computer Science
- Masters in Computer Science
Practice Problems
Q1. Who invented the merge sort algorithm?
- Leonard M. Adelman
- Frances E. ACM-SIAM
- Timothy J. Berners
- John von Neumann
Answer- Option d
Explanation- John von Neumann invented merge sort.
Q2. How is an array sorted in merge sort?
- An array is divided into 2 equal parts.
- An array is divided into a given ratio.
- An array is kept as a whole.
- All of these
Answer- Option a
Explanation- In the merge sort, an array is divided into two halves.
Q3. Which type of sort is used with a smaller array size?
- Radix Sort
- Merge sort
- Quick sort
- None of these
Answer- Option c.
Explanation- Quick sort is the most efficient way to sort smaller array sizes
Q4. Which type of sort is used with a bigger array size?
- Radix sorting algorithm
- Merge sort
- Quick sorting algorithm
- int n1 sorting algorithm
Answer- Option b
Explanation- Merge sort is the most efficient way to sort bigger array sizes.
Q5. Merge sort algorithm follows which type of approach?
- Comparison of extra space.
- int end addition.
- Divide and conquer.
- Multiplying numeric data.
Answer- Option c
Explanation- Merge sort algorithm splits the given problem into sub-problems to find the solution. Hence, it follows the divide-and-conquer approach to obtain a sorted array or list.
Common Mistakes
Merge sort is based on divide-and-conquer technique. It has better performance compared to brute force sorting technique like bubble sort.
Related Concepts
- Bubble Sort
- Insertion Sort
- Quick Sort
- Selection Sort
- Heap Sort
- Counting Sort
Want more help with your computer science homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Merge sort Homework Questions from Fellow Students
Browse our recently answered Merge sort homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.