What is Modulus Operator?
Modulus can be represented either as (mod or modulo) in computing operation. Modulus comes under arithmetic operations. Any number or variable which produces absolute value is modulus functionality. Magnitude of any function is totally changed by modulo operator as it changes even negative value to positive.

Operators and Operands
Operands may be any kind of lexical or special tokens (variables, constants etc.,). They can be the constructs that behave like a function which differs in semantics and syntax. That which gives the value function for operands are operators. There are different operators as lined up:
- Arithmetic
- Logical
- Assignment
- Bitwise
- Relational
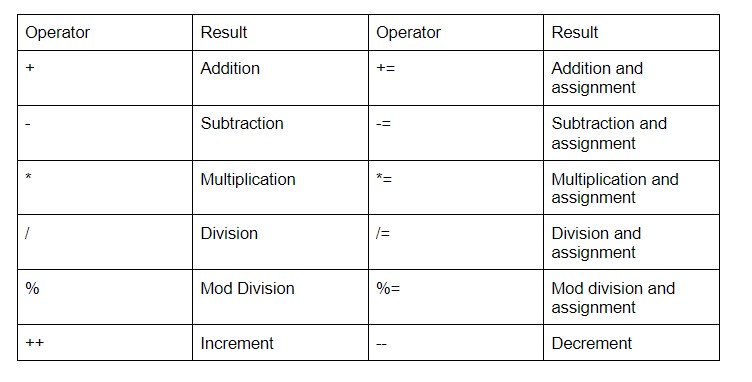
Arithmetic operator accounts for addition (+), subtraction (-), multiplication (*), division (/) and modulo (%).
Arithmetic operators allow manipulation of data.
- Unary type.
- Binary type.
Modulo Operator
The modulo operator is represented by the symbol (%). In computational operations, when a function returns the remainder or signed remainder if one integer is divided by another is the modulo operator function. Since it is working on integers ,it is called integer remainder operator.
Modulo is a binary operator (operand operator operand) having a left to right associativity. Operators which can work with two operands are binary operators.
Simple modulo operator can be represented as x % y where x and y are two integers. Short hand operator can be represented as x% =y.
The range of numbers for whole number modulo of n is zero to n − one inclusive (a mod one is usually zero; a mod 0 is indefinite, probably leading to a division by zero error in some scripted languages).
Why do we Opt Modulo Operator?
- Modulo operations provide bit wise Operation where tedious integers or decimal outs can be performed which can be mainly used in stack overflow.
- Whenever a linear data structure has to be converted into matrix integers, then there we can use modulo function.
- When we go for wrapping around that is wrapping values for infinite loop process, we can use modulo operator.
- Modulo can be used in cryptographic encryption and decryption, where the finite fields need to be converted into symmetric key algorithms.
Identities as cryptographic proofs:
Identity:
- (x mod m) mod m = x mod m.
- mx mod m = 0 for all positive integer values of x.
- If p denotes prime number which is indivisible by y, then xyp−1 mod p = x mod p, due to Fermat's little theorem.
Distributive:
- (x + y) mod m = [(x mod m) + (y mod m)] mod m.
- xy mod m = [(x mod m)(y mod m)] mod m
Inverse:
[(−x mod m) + (x mod m)] mod m = 0.
y−1 mod m can be noted as the standard inverse, that is outlined if and providing y and m are comparatively prime, that is that the case once the left aspect is defined: [(y−1 mod m)(y mod m)] mod m = 1.
Inverse multiplication:
[(xy mod m)(y−1 mod m)] mod m = x mod m
Division (definition):
(x/y)mod m = [(x mod m)(y−1 mod m)] mod m, when the right hand side is defined (that is when y and m are coprime).
Modulus on negative numbers:
It actually ignores the minus sign. Sign precedence is unfollowed. Left operand sign is appended to the result.
int main()
{
// x positive and y negative.
int x = 2, y = -13;
printf("%d", x % y);
return 0;
}
Output : 1
int main()
{
// x negative and y positive.
int x = -2, y = 13;
printf("%d", x % y);
return 0;
}
Output : -1
int main()
{
// x negative and y negative.
int x = -2, y = -13;
printf("%d", x % y);
return 0;
}
Output: -1 Let us see with an example:
Modulo Operator in Python
Numeric data types like int and float uses modulo operator.
Syntax: x% y
When x is divided by y, remainder is returned since it is a modulo operation.
Modulo Operator (int):
When two positive integers are divided, the integer remainder is given by modulo function.
Example:
>>> 27 % 5
2
>>>263%43
5
Program
for number in range(1, 100):
if(number % 5!= 0):
print (number)
Modulo Operator(float):
Example:
>>>27.6% 5.5
0.1
An alternative option instead to use in floating is math.fmod()
>>> import math
>>> math.fmod(27.6, 5.5)
0.1
Rounding off and precision issues can be occurred in math.fmod() when it deals with floating point.
>>> 15.3 % 1.1
0.09999999999999964

>>> import math
>>> math.fmod(15.3, 1.1)
0.09999999999999964
Negative operands modulo function:
Ambiguity is being left out for negative operand. It may vary for different programming languages. If the dividend is positive and divisor is negative, programming languages takes only divisor sign as remainder sign.
In Java script and java truncated function is used to reclaim the same remainder along with divisor sign.
But in python, floor division is used.
r = 36 - (-5 * floor (36/-5))
r = 36 - (-5 * floor (-2.666666666667))
r = 36 - (-5 * -5) # Rounded away from 0
r = 36 - 25
r = 7
Time Complexity of Modulus Operation
Runtime of modulus operator (%) is
O((logn)2).
Modulus Operation gives variation on division, that enhances fixed - sized numbers with constant time.
There exists O (1) for inside loop operations that makes total complexity as O(√n).
For large integers it is O(n2) and unsigned modulo integer is O(MN).
Restrictions of a modulus operator:
Only integral operands can use modulo operation. Float or double cannot use modulo operation. The reason is modulus instructions are not provided for floating point numbers in high level programming languages (C, C++).
But this accounts for a different behavior in Java as it uses modulo for floating point numbers.
The results of a floating-point remainder operation are set by the foundations of IEEE arithmetic:
If either quantity is NaN(Not a Number ), the result's NaN.
If the result's NaN, the sign of the result equals the sign of the dividend.
If the dividend is associate degree time, or the divisor may be a zero, or both, the result's NaN.
If the dividend is finite and also the divisor is associate degree time, the result equals the dividend.
If the dividend may be a zero and also the divisor is finite, the result equals the dividend.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- B.Sc. Computer
- M.Sc. Computer
Want more help with your computer science homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Modulus Operator Homework Questions from Fellow Students
Browse our recently answered Modulus Operator homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.