A linked lists are one of the most widely used and effective data structures, with applications in every programming language, including C, C++, Python, Java, and C#.
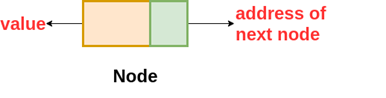
A linked list is a type of linear data structure in which the elements are not stored in consecutive memory locations. Instead, each element points to another. It is a data structure made up of nodes that represent a sequence. Linked lists are linear data structures that store information in individual objects known as nodes. These nodes contain data as well as a reference to the next node in the list. Because of their ease of insertion and deletion, linked lists are frequently used. Stacks, queues, and other abstract data types can be implemented using them. A linked list's elements are linked using pointers, as shown in the image below:

Linked List Types
The types of linked lists are as follows:
- Singly Linked List.
- Doubly Linked List.
- Circular Linked List.
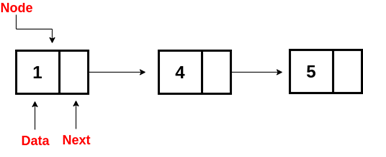
- Singly Linked List
A singly-linked list is a collection of nodes linked together in a proper sequence, with each node containing a data field and an address field usually contains the reference to the next node. It can be traversed both forward and backward.
The structure of the Singly Linked List node is
class Node {
int data // variable to store the data of the node
Node next // variable to store the address of the next node
}
The nodes are linked together in this way, where the value of the last node's next variable is NULL, i.e. next = NULL, indicating the end of the linked list.
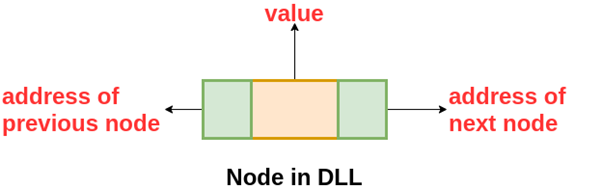
- Doubly Linked List
A doubly linked list has extra memory to store the previous node's address, as well as the next node's address and data, which are present in a singly linked list. So, we're storing the addresses of the next and previous nodes here.
The structure of the node in the Doubly Linked List (DLL) is as follows:
class DLLNode {
int val // variable to store the data of the node
DLLNode prev // variable to store the address of the previous node
DLLNode next // variable to store the address of the next node
}
The nodes are linked in the following way: the first node has prev = NULL and the last node has next = NULL.

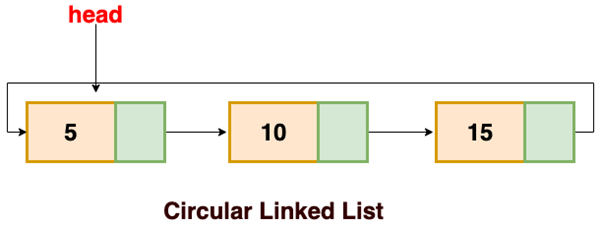
- Circular Linked List
A circular linked list is a singly or doubly linked list that contains no NULL values. We can use Singly or Doubly Linked Lists to implement the Circular Linked List in this case. In the case of a singly linked list, the next of last node contains the address of the first node, and in the case of a doubly-linked list, the next of last node contains the address of the first node and the address of the first node's preceding node contain the address of the last node. From any node, the list can be traversed.
Basic Operations on Linked List
- Traversal: The process of going from one node to the next.
- Insertion: The addition of a node at the specified position.
- Deletion: The act of removing a node.
- Searching: To look for an element(s) based on its value.
- Updating: To bring a node up to date.
- Sorting is the process of arranging nodes in a linked list in a specific order.
- Merging: The process of combining two linked lists into one.
The structure of a linked list node is as follows:
class Node{
int data // variable containing the data of the node
Node next // variable containing the address of next node
}
1.1.1.1 Linked List Traversal
1.1.1.2 The goal here is to work your way through the list from beginning to end. For instance, we might want to print the list or search for a specific node within it. The traversal algorithm for a list. Begin at the top of the list. If the head node is not null, you can get at its content. Then proceed to the next node (if one exists) and obtain node information. Continue until there are no more nodes (that is, you have reached the null node)
void traverseLL(Node head) {
while(head != NULL)
{
print(head.data)
head = head.next
}
}
1.1.1.3 Linked List node Insertion
When we insert a node into a linked list, one of three things can happen.
- Insertion at the beginning
- Insertion at the end. (Append)
- Insertion after a given node
Insertion at the beginning- Because there is no need to locate the end of the list. If the list is empty, we make the new node the list's head. Otherwise, we must connect the new node to the current head of the list, making the new node the list's head.
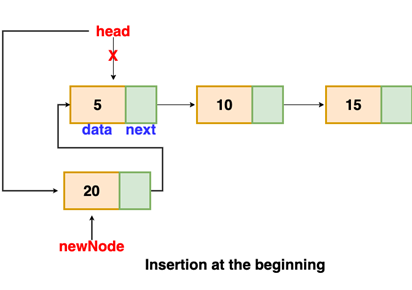
// function is returning the head of the singly linked-list
Node insertAtBegin(Node head, int val)
{
newNode = new Node(val) // creating new node of linked list
if(head == NULL) // check if linked list is empty
return newNode
else // inserting the node at the beginning
{
newNode.next = head
return newNode
}
}
Insertion at end- We'll go through the list until we get to the end. The new node is then added to the end of the list. It is worth noting that we must account for special cases such as the list being empty. If a list is empty, we will return the updated head of the linked list because the inserted node is both the first and last node in the linked list.
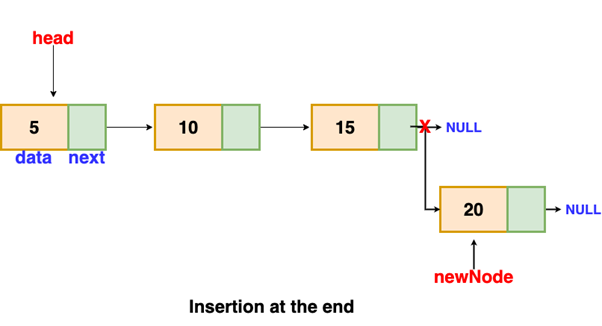
// the function is returning the head of the singly linked list
Node insertAtEnd(Node head, int val)
{
if( head == NULL ) // handing the special case
{
newNode = new Node(val)
head = newNode
return head
}
Node temp = head
// traversing the list to get the last node
while( temp.next != NULL )
{
temp = temp.next
}
newNode = new Node(val)
temp.next = newNode
return head
}
Insertion after a given node- We are given a node reference, and the new node is added after the given node
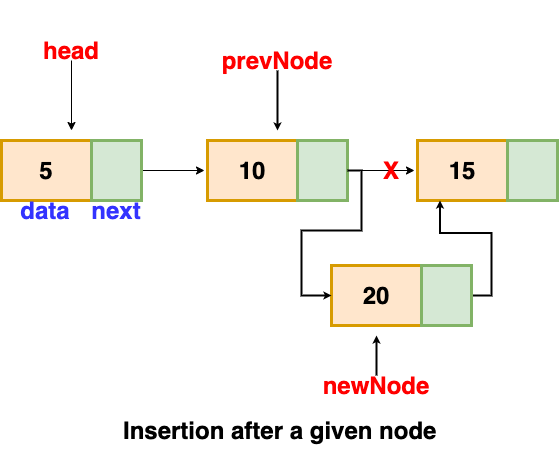
void insertAfter(Node prevNode, int val)
{
newNode = new Node(val)
newNode.next = prevNode.next
prevNode.next = newNode
}
1.1.1.5 Linked List node Deletion
To delete a node from a linked list, follow these steps.
o Find the node preceding the one to be deleted.
o Change the previous node's next pointer.
o Free the deleted node's memory.
o There is a special case in which the first node is deleted during the deletion. In this case, we must update the linked list's head.
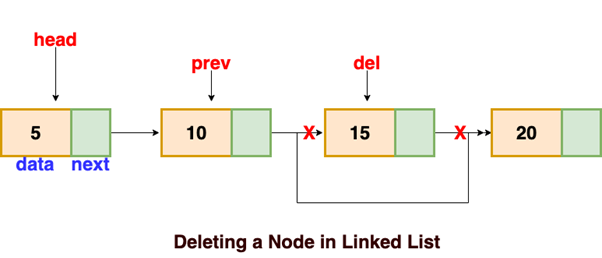
// this function will return the head of the linked list
Node deleteLL(Node head, Node del)
{
if(head == del) // if the node to be deleted is the head node
{
return head.next // special case for the first Node
}
Node temp = head
while( temp.next != NULL )
{
if(temp.next == del) // finding the node to be deleted
{
temp.next = temp.next.next
delete del // free the memory of that Node
return head
}
temp = temp.next
}
return head // if no node matches in the Linked List
}
Time and Space Complexity
Time- Linked lists are most useful when it comes to inserting and removing nodes from the list. In contrast to the dynamic array, insertion and deletion at any point in the list take the same amount of time.
However, unlike dynamic arrays, accessing the data in these nodes takes linear time due to the need to traverse the entire list using pointers. It's also worth noting that there's no way to optimise search in linked lists. We could at least keep the array sorted in the array. However, because we don't know how long the linked list is, we can't perform a binary search:
Space- Each node in a linked list contains two pieces of information (the value and the pointer). This means that the amount of data stored grows in a linear fashion as the number of nodes in the list grows. As a result, the linked list's space complexity is linear:
Common Mistakes
- Sometimes student make loops in structures so it leads to crash of methods
- When manipulating linked lists in-place, it is critical to avoid using values that have been invalidated in previous assignments.
Context & Applications
- Stacks and queues are implemented.
- Graph implementation: The most common graph representation is the adjacency list, which uses a linked list to store adjacent vertices.
- We use a linked list of free blocks for dynamic memory allocation.
- Maintaining a name directory
- Using long integers to perform arithmetic operations
Real-world Applications of Linked Lists-
- Image viewer – Because the previous and next images are linked, they can be accessed using the next and previous buttons.
- Previous and next page in web browser – Because they are linked as a linked list, we can access the previous and next url searched in web browser by pressing the back and next buttons.
Related Concepts
- Node Updating
- Node Searching
- Stacks
- Queues
Want more help with your computer science homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Operations of Linked List Homework Questions from Fellow Students
Browse our recently answered Operations of Linked List homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.