What is Sorting?
Sorting is a technique used to arrange items or objects in a specific order which can be ascending or descending. It simply refers to the storage of data in a sorted sequence. It organizes the data in a logical order to facilitate searching.
Sorting Techniques
The method of sorting is determined based on the situation. It is determined by two factors.
1. The term "execution time" refers to the amount of time it takes for a program to run.
2. The term "space" refers to the amount of space occupied by the software.
Sorting methods differ in terms of efficiency and space needs.
Different Sorting Algorithms
There are a variety of sorting techniques available, each with its efficiency and space needs. The following are some of the widely used sorting techniques.
- Bubble sort
- Insertion sort
- Selection sort
- Merge sort
- Heap sort
This algorithm needs inputs. After taking inputs, it works on the inputs and processes them. And at the end, it generates the result. Some of the examples are here:
Bubble Sort Algorithm
- A bubble sort is a type of sorting that is used to sort elements by bubbling up the largest element in the array so that it occupies its correct position in the sorted array. It then bubbles up the second largest element and so on till the array is sorted.
- It compares each element individually and arranges them according to their values.
Implementing Bubble Sort Algorithm
These are the steps that are used in bubble sort.
- Compare the current element to the next element of the array, starting with 0 index element.
- If the current element > next element then swap both elements.
- If condition 2 is not true then move on the next element. Step 1 should be repeated.
Consider an array having the values {14,33,27,35,10}
This example shows the working process of the bubble sort algorithm.
| 14 | 33 | 27 | 35 | 10 |
First Pass:
- Compare the first Arr[0] and second elements Arr[1]. Here Arr[0] (value is 14) is not greater than Arr[1] (value is 33) so there is no value swapped. and the array remains unchanged.
| 14 | 33 | 27 | 35 | 10 |
- Then move on to the second Arr[1] and third elements Arr[2]. Check Arr[1] and Arr[2] that means 33 > 27, which is correct. As a result, Arr[1] and Arr[2] are swapped.
| 14 | 33 | 27 | 35 | 10 |
As a result, the array becomes:
| 14 | 27 | 33 | 35 | 10 |
- Arr[2] and Arr[3] are the third and fourth elements, respectively. If 33 is greater than 35, this is a misleading result. As a result, there is no swapping and the array is unchanged.
| 14 | 27 | 33 | 35 | 10 |
- Now to go on to the fourth Arr[3] and fifth elements Arr[4]. Check 35>10, which is true. As a result, Arr[3] and Arr[4] are swapped.
| 14 | 27 | 33 | 35 | 10 |
As a result of the switch, the array now looks like this:
| 14 | 27 | 33 | 10 | 35 |
So, at the end the greatest element is set to last position. Signaling the end of the first pass.
Second Pass:
In a second pass compare 14 and 27
| 14 | 27 | 33 | 10 | 35 |
compare 27 and 33
| 14 | 27 | 33 | 10 | 35 |
compare 33 and 10, 33 greater than 10 so exchange the position
| 14 | 27 | 33 | 10 | 35 |
| 14 | 27 | 10 | 33 | 35 |
compare 33 and 35
| 14 | 27 | 10 | 33 | 35 |
Continue this for third pass and the result is
| 14 | 10 | 27 | 33 | 35 |
In fourth pass the result is
| 10 | 14 | 27 | 33 | 35 |
i-th Pass
If the array has i-th places then the largest element is stored at the i-th place after executing the i-th pass.
n-th Pass:
After completing all of the passes, it is noticed that the array has been sorted.
As a result, the sorted array will appear as follows:
| 10 | 14 | 27 | 33 | 35 |
Insertion Sort Algorithm
- This method sorts the array by shifting each element one at a time.
- The resulting sorted array is constructed by adding one element at a moment.
- This sort is good for tiny data sets, but it is not suitable for long lists.
Implementing Insertion Sort Algorithm
- In the first step of the insertion sort algorithm, compare the element that is present in the question with its neighbor's elements.
- on each comparison, the place of the element is found out and it is place at that position, by shifting the remaining elements to right.
- The process is continued until all of the array's elements are correctly placed.
Let's take an example: 25, 17, 31, 13, 2
Here is the solution of the insertion sort.
Initial Iteration:
When comparing 25 to 17, see the difference. 17 25 is the result of the comparison. As a result, exchange 17 and 25.
This is how the array now looks:
| 25 | 17 | 31 | 13 | 2 |
| 17 | 25 | 31 | 13 | 2 |
Second Iteration:
Go to the second element, however, it has already been moved to its proper location, therefore go to the following element. Consider the third element (31) and how it compares to the previous ones.
There is no swapping since 31> 25.
Furthermore, when 31> 17, no switching occurs, and 31 remains in its original location.
After the second iteration, This is how the array appears:
17, 25, 31, 13, 2
| 17 | 25 | 31 | 13 | 2 |
Third Iteration:
Iterate the fourth element (13), and compare it to the previous items.
Swapping the two since 13<31. The array is now: 17, 25, 13, 31, 2.
However, there are still certain aspects that have not been compared to 13. Between the ages of 25 and 13, the comparison now takes place. As a result, since 13<25, the condition is true then swap the two elements. After this, the array becomes 17, 13, 25, 31, 2.
The last comparison is 17 and 13. It has been swapping the two since 13<17. The array now becomes 13, 17, 25, 31, 2.
| 13 | 17 | 25 | 31 | 2 |
Continue for Fourth Iteration-
| 2 | 13 | 17 | 25 | 31 |
The final array is: 2, 13, 17, 25, 31. So this is the resultant array.
Selection Sort Algorithm
The simplest sorting algorithm is the selection sort. In the selection sort algorithm, first of all, Pick the smallest element of the array. Swap the smallest element with the array's initial element. After this pick the second minimum element. And then move this to the array's second place. Continue to this process and at the end the array becomes sorted. Selection sort is named for the fact that it constantly selects the next-smallest element and swaps it into the correct position.
Implementing Selection Sort Algorithm
When sorting the array using selection sort, the unsorted array is distributed into two categories. The first category is a sorted array and the second category is an unsorted array. The left subarray is a sorted array and the right subarray is an unsorted array. At the starting condition, the left array is empty. And right (unsorted subarray) contains all elements of the array.
A user repeats the following steps until the unsorted subarray is empty:
1. From the unsorted subarray, select the smallest entry.
2. Replace it with the unsorted subarray's leftmost element.
3. The unsorted subarray's leftmost element has been incorporated into the sorted subarray and is no longer involved of the unsorted subarray.
Take an example array {5, 2, 6, 7, 2, 1, 0, 3}.Below is a graphic example of selection sort.
Consider the diagram below to depict various arrays.
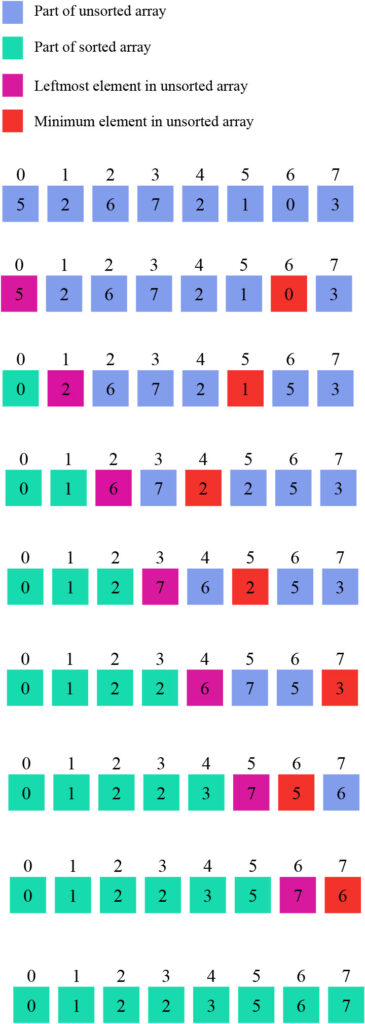
Initial array A = [5, 2, 6, 7, 2, 1, 0, 3]
Unsorted subarray leftmost element = A[0]
Smallest element present in unsorted array = A[6]
At the first, A[0] and A[6] elements are swapped to each other and make a sorted array A[0] on the left side.
Now, the unsorted array leftmost element = A[1]
Smallest element present in unsorted array = A[5]
A[1] and A[5] elements are swapped to each other and make a sorted array A[1] on the left side.
Unsorted subarray leftmost element = A[2]
Smallest element present in unsorted array = A[4]
A[2] and A[4] elements are swapped to each other and make a sorted array A[2] on the left side.
Continue this

This is the final sorted array.
Merge Sort Algorithm
Divide and conquer technology is used in the merge sort algorithm. This technology saves a lot of time. The benefit of the divide and conquer technology is that the single element in the array is always sorted by itself. It divides the array according to its size. Each element becomes a separate array. Then it repeatedly merges these subarrays to create new sorted subarrays, until one complete sorted array is produced.
Implementing Merge Sort Algorithm
The steps for merging sort are as follows:
1. First of all assume a variable p and give it the first index of array. Then, in a new variable called r, store the last index of the array.
2. Now apply the formula (p + r)/2. This gives the middle point of the array. q should be assigned to the middle index. and then the array is divide into two parts. The first part contains p to q elements and the second part contains q+1 to r index elements.
3. After this, the created array is further divided into two subarrays following the above manner. And repeat this process.
Merge sort representation is here.
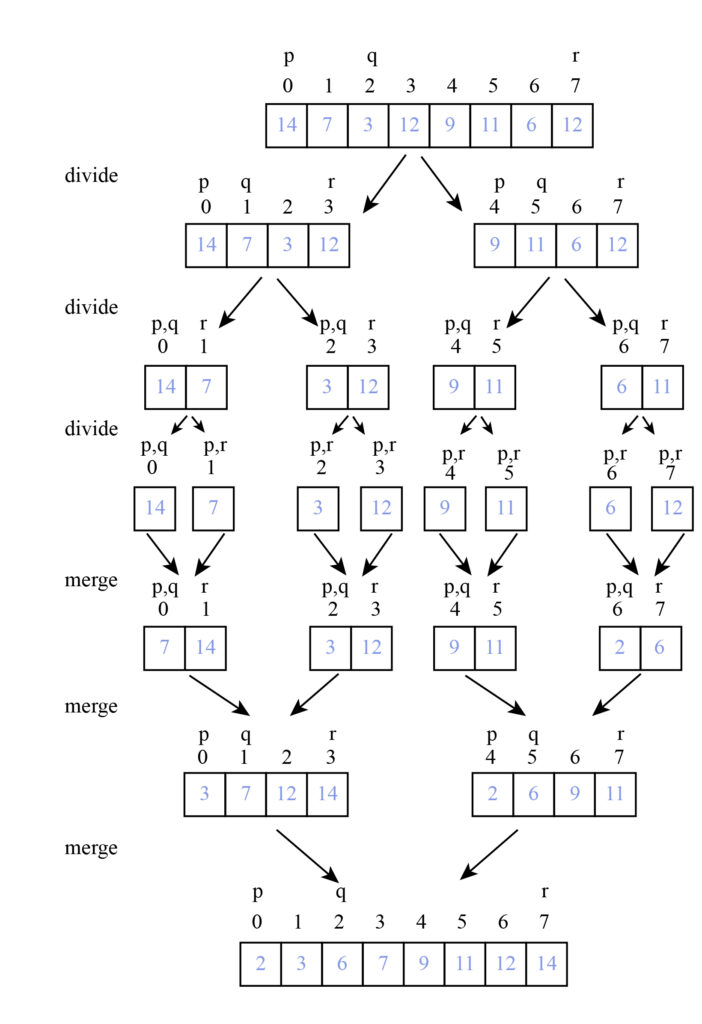
Heap Sort Algorithm
- Heap sort follows tree data structure. A comparison-based sorting algorithm is used in this approach.
- It resembles the selection sort algorithm quite closely. The main difference is that it searches for the largest element in an array and store it in the last place.
Implementing Heap Sort Algorithm
According to the figure, the unsorted array having length 6 is created first, followed by a max-heap.
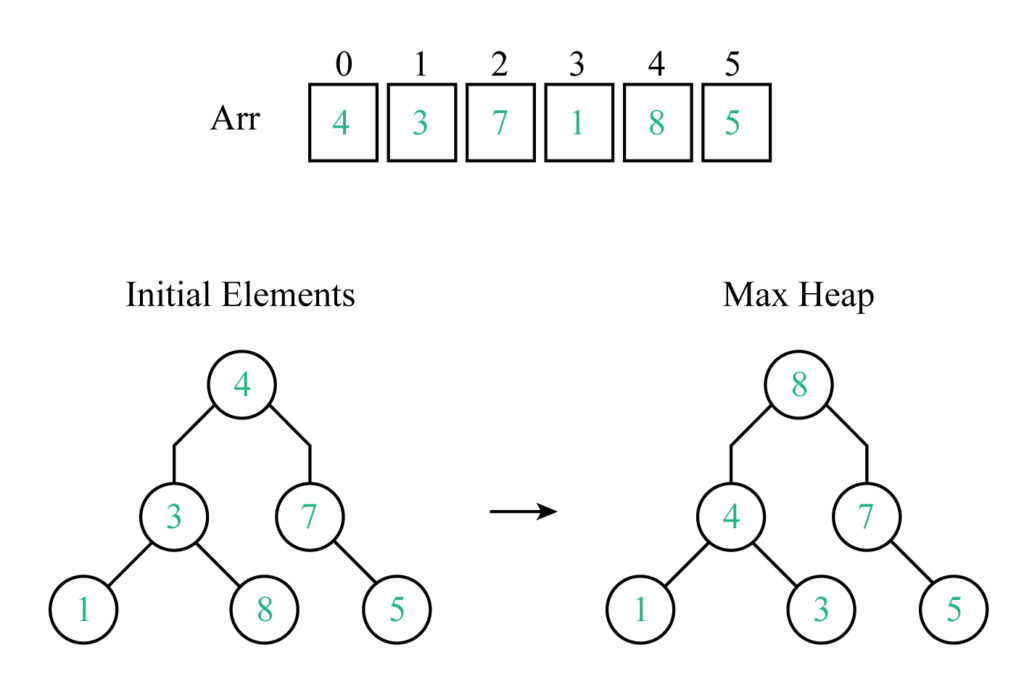
Following the construction of max-heap, the array Arr will be:
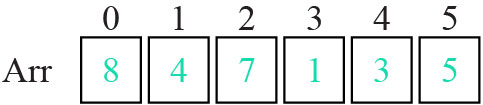
Follow the below steps for Heap Sorting:
Step 1: First find the largest element. Here is 8. and compare it with the last element of the array. Here is 5. Here 8>5 then swap it.
Step 2: After performing the swapping element 8 is to remove from removed the heap. Thus 8 is located in its correct position.
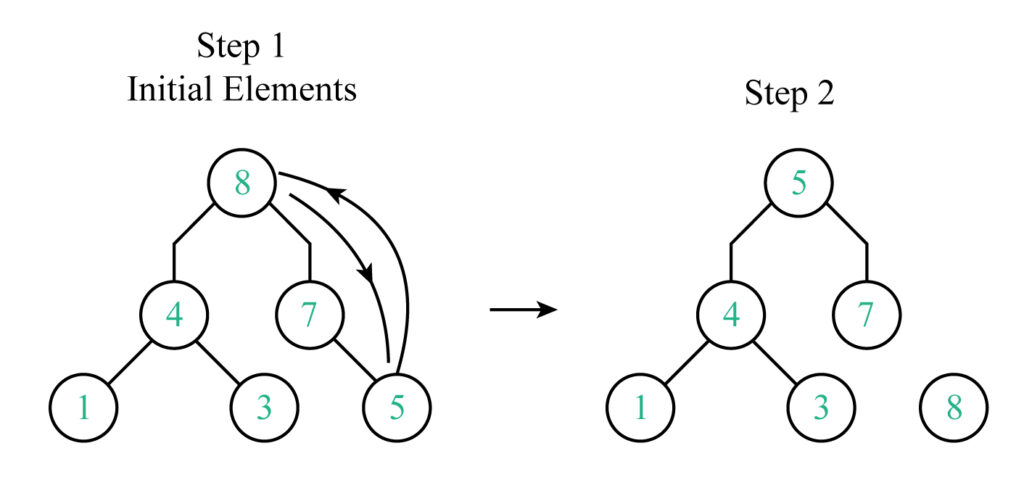
Step 3: In the third step Max-heap is developed. The value 7 is swapped by the the value 3.
Step 4: The value 7 has been set its correct position so it is remove from the heap.
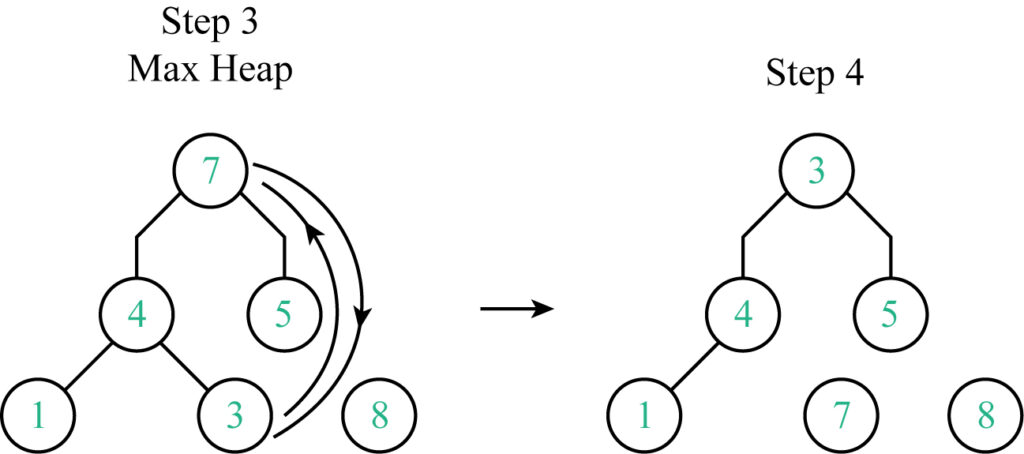
Step 5: In the fifth step value 5 is swapped by the value 1.
Step 6: The value 5 has been set in its correct position so it is removed from the heap.
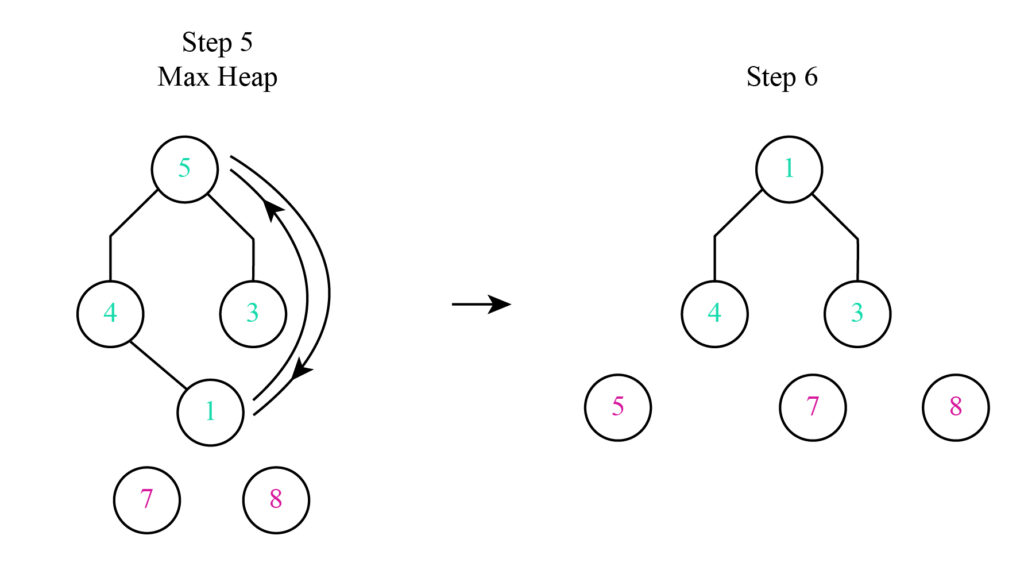
Continue this
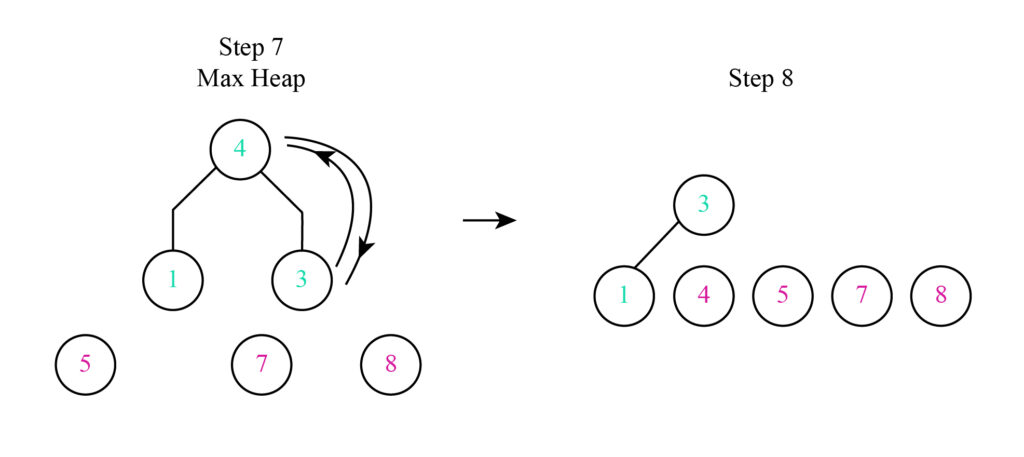
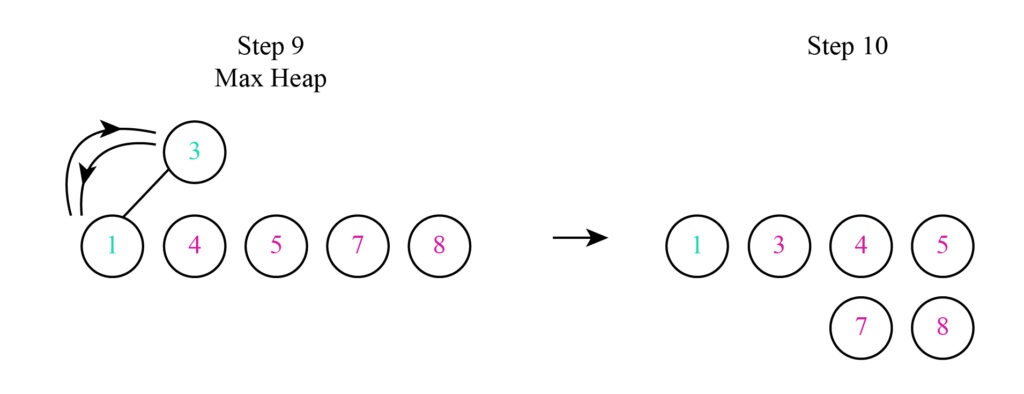
The final array is developed after performing all the steps.
Comparision of Sorting Algorithm
- If a sorting algorithm does not need additional space to change the input but does need a modest but non-constant amount of additional space to execute, it is called in-place. If just a small element from the input array would ever be stored from outside array, the sorting algorithm is said to sort in-place.
- A stable sorting algorithm does not need to change elements orders with same values.
| Sorting Algorithm | Time Complexity | Space complexity | In-Place | Stable | ||
| Best case | Average case | Worst case | Worst case | |||
| Bubble sort | Yes | Yes | ||||
| Selection sort | Yes | No | ||||
| Insertion sort | Yes | Yes | ||||
| Merge sort | No (Its needs a additional storage for merging the sorted subarray. ) | Yes | ||||
| Heap sort | Yes | No | ||||
Application of Sorting Algorithm
There are a lot of application of different sorting algorithm.
| Sorting Algorithm | Application |
| Bubble Sort |
|
Insertion Sort |
|
| Selection Sort |
|
| Merge Sort |
|
| Heap Sort |
|
Common Mistakes
There is no such thing as a "best" or "worst" sorting algorithm. Each algorithm has its own set of applications. Also, depending on the magnitude of the input data, the same algorithm may behave differently. The first step in selecting a sorting solution is to identify the problem space as well as requirements. When a single algorithm fails to meet the requirements, a hybrid method offers a superior result. After the user has determined the issue space narrow down the list of possible good-enough algorithms and do a practical analysis on the input data to arrive at a final solution.
Context and Applications
This topic is significant in the professional exams for graduate and postgraduate courses,
especially for
- Bachelor of Science in Information Systems.
- Bachelor of Science in Computer Science.
- Master of Science in Data Analytics.
Related Concepts
- Insertion sort
- Time complexity
- Asymptotic Analysis
- Quick sort
- Comparison of sorting algorithm
- Tree sort
Practice Questions
Q.1 Which of the following real-world scenarios uses insertion sort?
(A) Putting books on a library shelf
(B) Database and distribution scenarios
(C) Arranging a pack of playing card
(D) Real-time systems
Correct Option: (C) arranging a pack of playing card
Explanation: A pack of cards is arranged to mimic an insertion sort. A database is a merge sort scenario, a stack is arranging books, and real-time systems employ quick sort.
Q.2 Which algorithms are recursive?
(A) Merge Sort
(B) Quick Sort
(C) Binary Search
(D) All of the above
Correct Option: (D) All of the above
Explanation: Merge sort, quick sort and binary search all algorithms are recursive. In sorting algorithms, recursive approaches can be used, allowing for the sorting of n elements in time (as opposed to the efficiency of bubble sort).
Q.3 Which sorting uses divide-and-conquer technique?
(A) Selection sort
(B) Bubble sort
(C) Insertion sort
(D) Merge sort
Correct Option: (D) Merge sort
Explanation: The merge sort algorithm is a typical divide and conquers strategy. Sort the left and right parts of an array independently before merging them to sort it recursively.
Q.4 What does sorting mean?
(A) Listing elements in Ascending or Descending order
(B) Keep the largest element first in the array
(C) Retrieve an item dataset
(D) All of the above
Correct Option: (A) Listing elements in Ascending or Descending order
Explanation: Any technique of systematically arranging elements is referred to as sorting. The arrangement is either ascending or descending.
Q.5 ---------------- is not a stable sorting technique.
(A) Merge Sort
(B) Bubble Sort
(C) Selection Sort
(D) Insertion Sort
Correct Option: (C) Selection Sort
Explanation: The sorting time is unaffected by the order of the items. So that the selection sort is not a stable sorting algorithm.
Want more help with your computer science homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Sorting Homework Questions from Fellow Students
Browse our recently answered Sorting homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.