What are strongly connected components?
A directed graph in which a path exists between all its pairs of vertices is called a strongly connected graph. A portion of the strongly connected directed graph that contains a path to reach from each vertex to other vertices is called a strongly connected component (SCC).
The concept of strongly connected components exists only for directed graphs. Every single vertex is a strongly connected component.
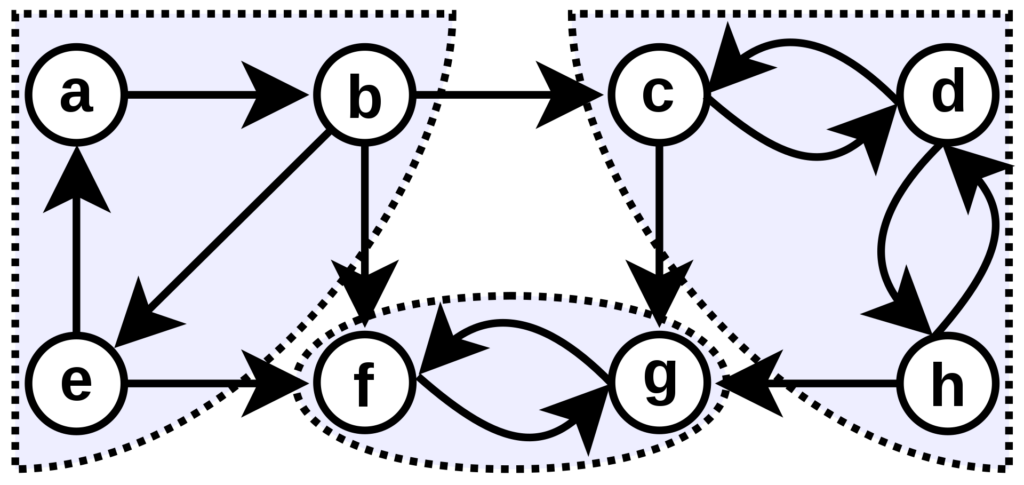
In the above graph, every strongly connected component is highlighted, and there are three strongly connected components in the graph.
There are mainly two algorithms to find the strongly connected components in a directed graph:
- Kosaraju's algorithm
- Tarjan's strongly connected components algorithm
Using DFS to find SCC
Algorithms used to find strongly connected components use the depth-first search (DFS) technique. This algorithm starts from the root node in the graph and traverses to all the nodes that are reachable from that node before backtracking. This states that the algorithm moves to the next unvisited node and moves further until no unvisited node is left. Then, it backtracks and visits other unvisited nodes. Ultimately, all the nodes are printed.
Now, to find out if a graph has an SCC, the DFS begins from any node in the graph and checks if all the other vertices in the graph are reachable or not. If all the vertices are reachable, then the graph is strongly connected. Otherwise, the subset of vertices that are reachable from the chosen vertex will be identified as the SCC.
Kosaraju's algorithm
Kosaraju's algorithm is a linear time graph algorithm for finding the strongly connected components in a directed graph. The algorithm uses DFS to find the SCCs in the graph.
Kosaraju's algorithm is based on the concept that if it is possible to reach a vertex v from u, then it is also possible to reach vertex u from v. If this condition is satisfied, it can be said that the vertices u and v are strongly connected.
Kosaraju's algorithm includes the following steps:
- Perform a depth-first search on the original directed graph - Start from one vertex and visit all its children, then mark the vertices as visited. Further, if another vertex leads to a visited vertex in the graph, push it to the stack.
- Change the direction of the edges in the graph by reversing each edge.
- Begin from the top of the stack and pop the vertices one by one. Then, perform DFS on the modified graph.
Example: Consider the directed graph shown below.
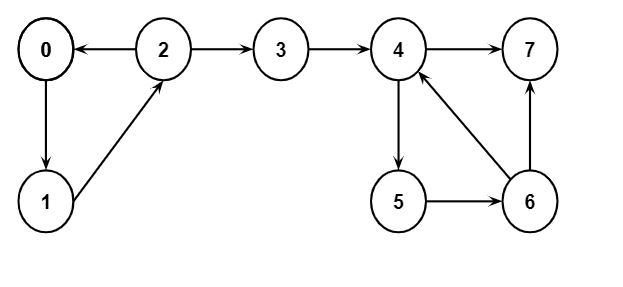
The process to find the SCC of the above graph will be as follows:
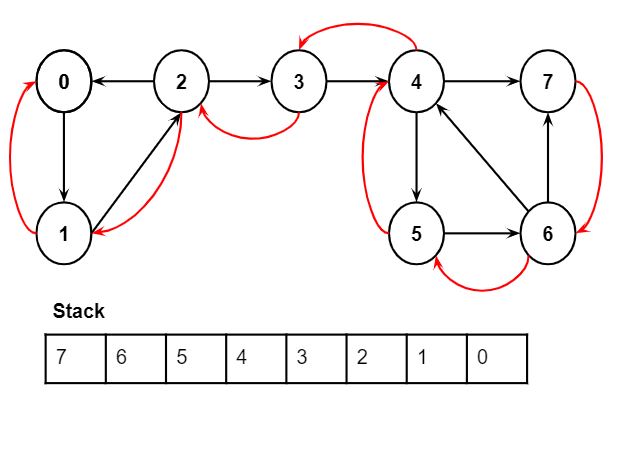
Step 1: Apply DFS on node 0 and go through all the outgoing edges from each unvisited node. Create an array to track the visited nodes and use a stack to store the nodes in the order in which their outgoing edges were tracked. The result will be as shown below:
Step 2: Reverse the original directed graph.
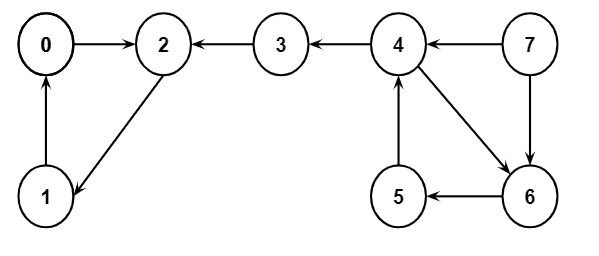
Step 3: Pop the stack elements one by one and perform a depth-first search on the reversed graph. Finally, the strongly connected components will be as follows:
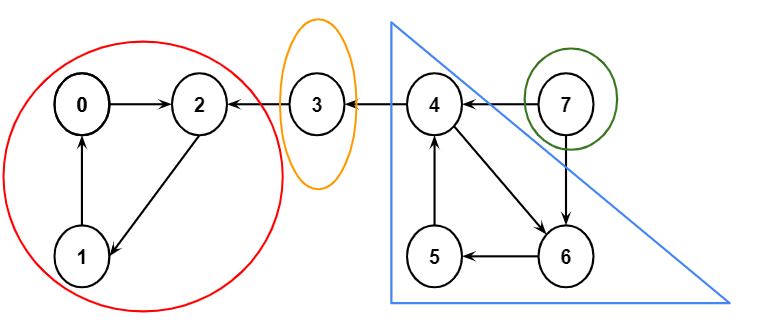
Here, each strongly connected component is shown in a different color.
Time complexity
Kosaraju's algorithm uses DFS twice to find the strongly connected components. It first performs DFS on the original graph in linear time O(V + E). Then, it performs DFS on the reversed graph, which again takes O(V + E) time. Hence, Kosaraju's algorithm's overall time complexity is O(V + E).
Tarjan's strongly connected components algorithm
Tarjan's strongly connected component algorithm finds the strongly connected components in a graph in linear time. Tarjan's algorithm takes a directed graph, divides the graph's vertices into the strongly connected components. Every node appears once in any of the strongly connected components, and any node that does not form a cycle forms an SCC itself.
The working of Tarjan's SCC algorithm is as follows:
- The algorithm performs a DFS on the vertices to remove and record subtrees of SCCs.
- Maintain two values DFS_num(u) and DFS_low(u), where DFS_num(u) will be the value of the counter when the vertex is visited for the first time and DFS_low(u) will store the lowest DFS_num that can be reached from u and is not a part of any other SCC.
- Add the visited vertices to the stack.
- Visit the unvisited children of the stack, and update the DFS_low(u).
- A node having DFS_low(u) == DFS_num(u) will be the first visited node in the strongly connected component. The rest of the nodes above that node in the stack will be popped from the stack and allotted a relevant strongly connected component number.
Example: Consider the directed graph having 3 strongly connected components as shown below. Every SCC is indicated with a circle and the pair (DFS_low(), DFS_num(u)) is shown along with the vertex.
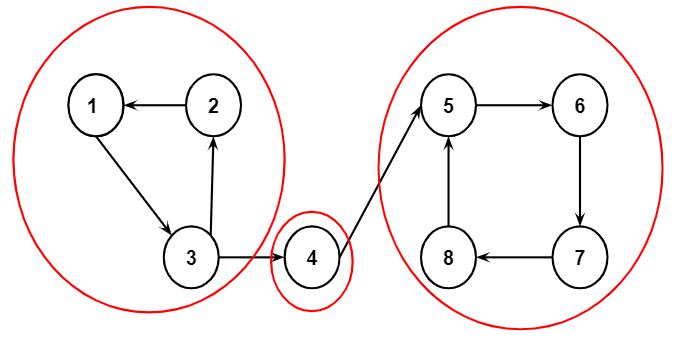
Now, let’s understand the working of Tarjan’s algorithm using the above graph.
Step 1: Call Tarjan’s algorithm on Node 1. Set the values of DFS_low[1] and DFS_num[1] to 1 and push node 1 to the stack.
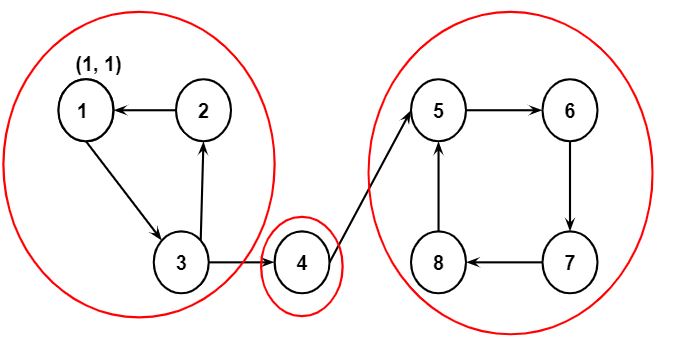
Step 2: Then values of DFS_low[2] and DFS_num[2] will be updated to 2 and node 2 will be pushed to the stack.
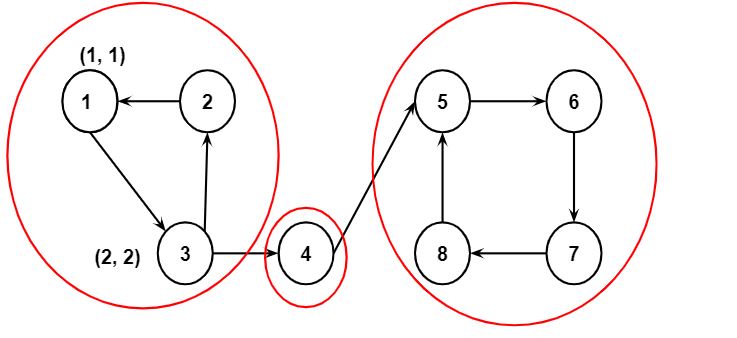
Step 3: Assume that node 4 is before node 2 in the adjacency list. Therefore, node 4 is called first. The values of DFS_low[4] and DFS_num[4] will be 3 and node 4 will be pushed to the stack.
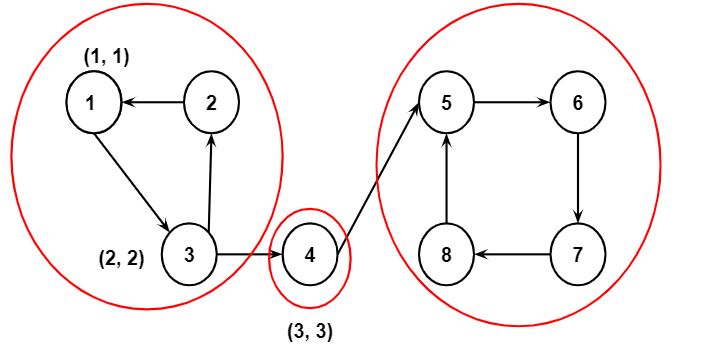
Step 4: Next, the values of DFS_low[5] and DFS_num[5] will be updated to 4, and node 5 will be pushed to the stack.
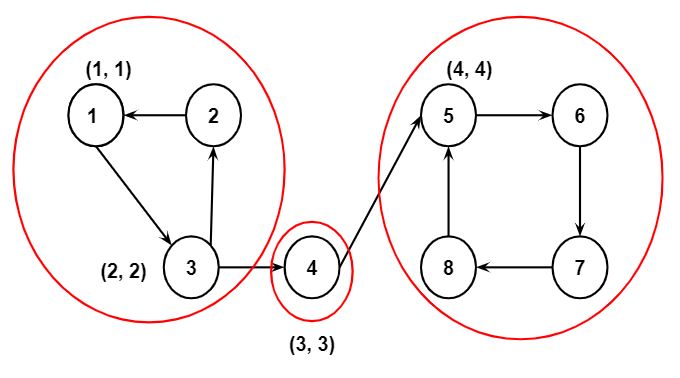
Step 5: Similarly, the values of DFS_low[6] and DFS_num[6] will be updated to 5, and node 6 will be pushed to the stack.
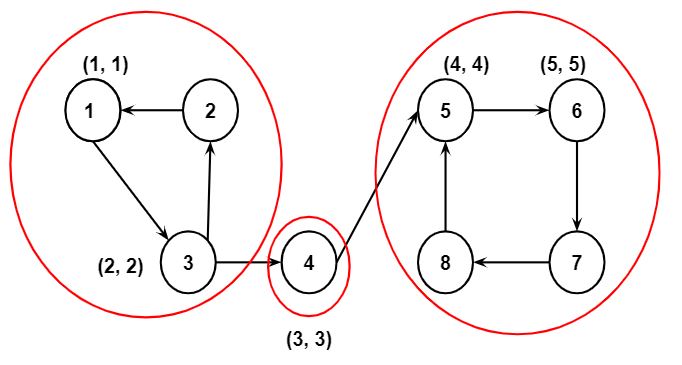
Step 6: Finally, the values of DFS_low[7] and DFS_num[7] will be updated to 6 and node 7 will be pushed to the stack and the values of DFS_low[8] and DFS_num[8] will be updated to 7 and node 8 will be pushed to the stack.
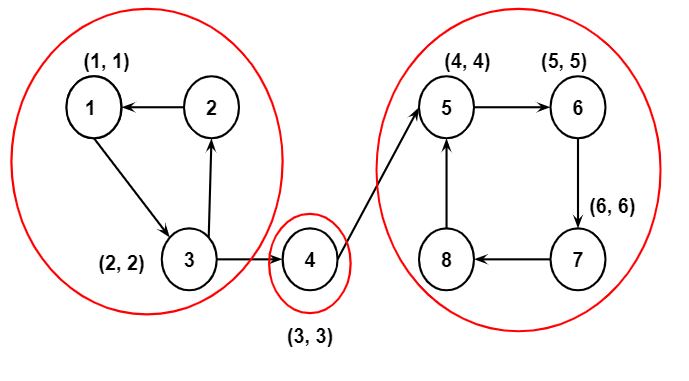
Step 7: Since node 5 is the first vertex having DFS_low()==DFS_num in the SCC, the values of DFS_low[8] will be updated to 4, DFS_low[7] will be set to 4, DFS_low[6] will be set to 4 and DFS_low[5] and DFS_num[5] will remain unchanged.
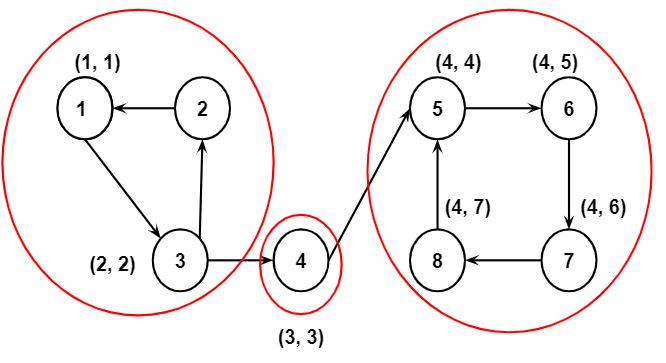
Step 8: The nodes above node 5 will be popped from the stack and the resultant SCC will be 5, 8,7,6.
Step 9: Similarly, for node 4, DFS_low[4] and DFS_num[4] will remain unchanged. The nodes above node 4 will be popped and the resultant SCC will be 4.
Step 10: Next, DFS_low[3] and DFS_num[3] will be updated to 8, and node 3 will be pushed to the stack.
Step 11: Due to node 1, DFS_low[3] and DFS_low[2] will be updated to 1.
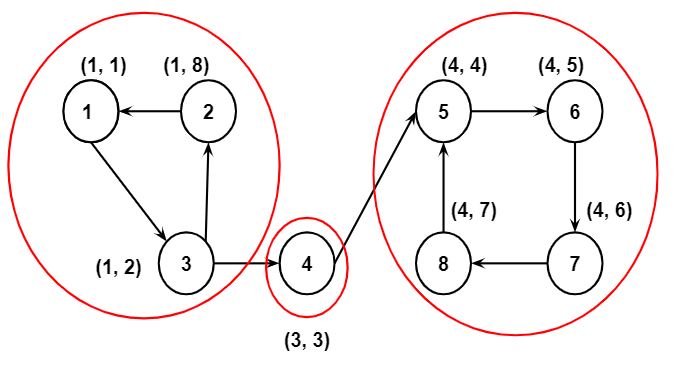
Step 12: DFS_low[1] and DFS_num[1] will remain unchanged. Then all the nodes above node 1 in the stack will be popped and the resultant SCC will be 1, 2, 3.
Time complexity: Tarjan's strongly connected components algorithm uses depth first search, so all the nodes are visited exactly once. Therefore, the algorithm takes a linear amount of time for execution, and the time complexity for this algorithm is O(V + E).
Applications of strongly connected components
Strongly connected components algorithms are widely used in various areas. These include:
- SCC algorithms are used in various graph algorithms, especially algorithms that need to work only on the SCC of a graph.
- SCC algorithms are used to find the similarities between a group of people on social networks. For example, the commonly liked pages, movies, or places.
- SCC algorithms are used in vehicle routing applications and maps.
- Tarjan’s SCC algorithm is used for transforming the graph into a directed acyclic graph of SCC. Tarjan’s SCC algorithm is used for solving boolean satisfiability problems in the data structure when the problem is unsatisfiable since the variable and component are in the same SCC.
Context and Applications
The concept strongly connected component is a part of the graph theory in data structures and algorithms. The topic is studied by students studying in courses like:
- Bachelors in Science in Information Technology
- Masters in Science in Information Technology
- Masters in Science in Artificial Intelligence
- Bachelors in Computer Science
- Masters in Computer Science
Practice Problems
Q1. In a directed graph, if there is a path from each vertex to every other vertex, it is called-
- Strongly connected
- Biconnected int vertex
- Disjoint reversed graph
- Weakly connected
Answer: Option a
Explanation: If there is a path from each vertex to another vertex in the graph, the graph is called strongly connected.
Q2. What is SCC?
- BFS or depth first search component
- Strongly decomposition component
- Strongly connected component
- Secured component
Answer: Option c
Explanation: SCC is the abbreviation for strongly connected components. An SCC is a part of a strongly connected graph in which there is a path from each vertex to every other vertex.
Q3. Which algorithm is used for finding SCC?
- Kosaraju’s
- Undirected
- Finish time
- Asymptotic depth first search
Answer: Option a
Explanation: Kosaraju’s algorithm and Tarjan’s strongly connected components algorithms are the two algorithms used for finding the SCC in a graph.
Q4. What is the time complexity of Kosaraju’s algorithm?
- Linear-time int v
- Biconnected finish time
- O(V + E)
- O(path algorithm)
Answer: Option c
Explanation: Kosaraju’s algorithm takes linear time to find the SCC in a graph. Hence, its time complexity is O(V + E), where V is the number of vertices and E is the number of edges.
Q5. Which of these is an application of SCC?
- Disjoint depth first search
- Dynamic Programming
- To find similarities between a group of people
- For graph algorithm sorting
Answer: Option c
Explanation: One of the applications of SCC is that it helps find the similarities between a group of people. It is mainly used on social networking sites.
Common Mistakes
The topics strongly connected graph and strongly connected components are different. Hence, students should not use these terms interchangeably.
Related Concepts
- Connected component (graph theory)
- Topological sorting
- Asymptotic analysis
- Dynamic programming
- Greedy algorithms
- Breadth-first search (BFS)
- Dijkstra algorithm
Want more help with your computer science homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Strongly Connected Components Homework Questions from Fellow Students
Browse our recently answered Strongly Connected Components homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.