What is Ampere’s circuital law?

Ampere's Law states that "for any closed loop path, the sum of the length elements times the magnetic field in the direction of the length element is equal to the permeability times the electric current enclosed in the loop.”

This means that the magnetic field by an electric current is proportional to the size of that electric current with a constant of proportionality equal to the permeability of the free space.

The equation for the ampere circuital law is given as:

$\oint B·dl={\mu }_{0}I$

where B is the magnetic field, dl is length element of the conductor, ${\mu }_0$ is permeability constant and I is the electric current.

Ampere’s Law

André-Marie ampère was a scientist who researched the forces at work in current cables. The experiment was going on in the late 1820s at the same time as Faraday was working on his Faraday law. According to Ampere’s law, the magnetic fields related to the electric field are generated. The law specifies the magnetic field related to the current given or vice versa, so long as the electric area does not change over time. Combining both their works, Maxwell introduced the equation which relates magnetic field with electric current

 The equation that is introduced is as follows:

$\nabla \times H=\frac{\delta D}{\delta t}+J$

where D is the electric flux density and J is displacement current density.

Displacement current density

Displacement current density in electromagnetism is established in a region where the electric field is not constant and changes with time. Mathematically it is written as

$J={\in }_0\frac{dE}{dt}$

where${\in }_0$ is permittivity constant, and E is the electric field.

How to determine Magnetic Field by Ampere’s Law?

Magnetic field due to long straight current wire

Consider an infinite long straight wire of a circular cross-section radius a carrying steady current I. The current is distributed uniformly across the cross-section.
Consider the case where the radius r is passing throught point P, where the magnetic field has to be determined.

The Amperes law will be written as

$\oint B·dl={\mu }_{0}I$

By symmetry B is same everwhere along the circle, hence the LHS of the equation can be written as

$$\begin{gathered} \oint B·dl=B\oint dl \\ \oint B·dl=B\left(2\mathrm{\pi r}\right) \end{gathered}$$

Hence by Amperes law, we can write

$$\begin{gathered} B\left(2\mathrm{\pi }r\right)={\mu }_{0}I \\ B=\frac{{\mu }_{0}I}{2\mathrm{\pi }r} \end{gathered}$$

Here, $B$ = magnetic field magnitude

${\mu }_0$ = permeability of free space

$I$ = magnitude of the electric current

$r$ = distance

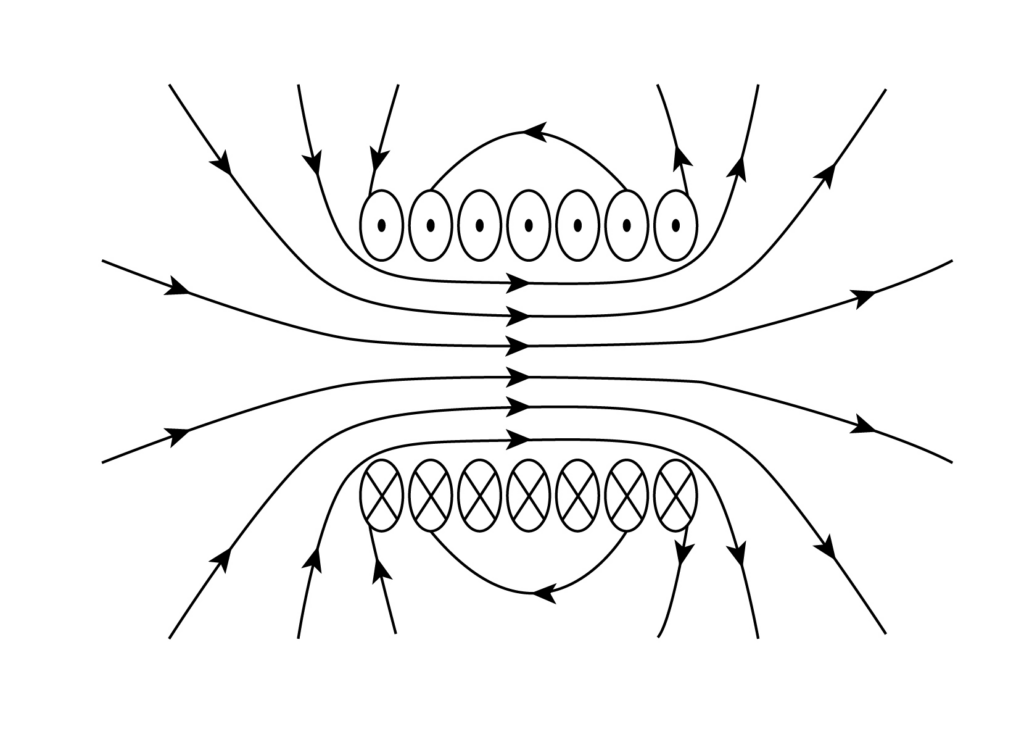
Magnetic field due solenoid

A solenoid is made by winding a large nuber of insulated wire over a box or clay. When the current is passed through the wire, magnetic field is produced within and around the solenoid. This magnetic field is calculated with the help of Amperes law and it turns out to be

$B={\mu }_{0}nI$

where n is the number of turns of wire (N) per unit length (L). 

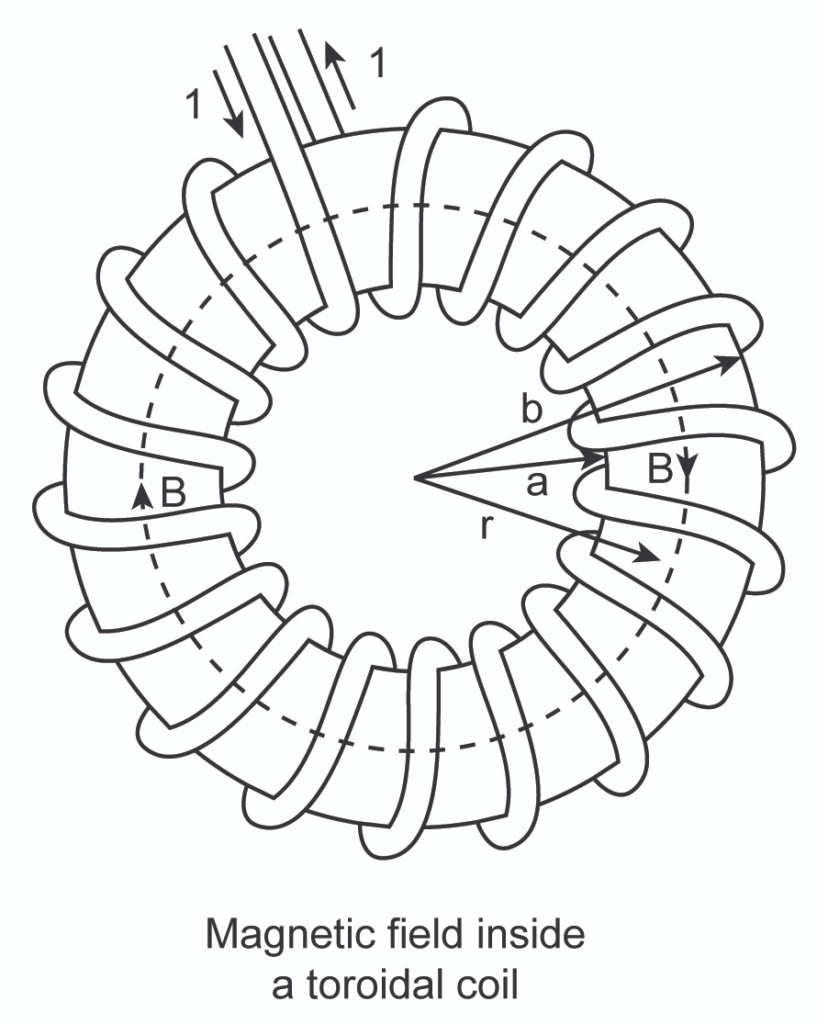
Magnetic field due toroid

A toroid is hollow ring made up of closely wounded insulated wires. It is basically a solenoid which is bent to for a circle. When the current is passed through the wire, magnetic field is produced within and around the toroid. This magnetic field is calculated with the help of Ampere's law and it turns out to be

$B={\mu }_{0}nI$

where n is given as $n=\frac{N}{2\mathrm{\pi r}}$, with N as the number of turns of wire and r as the radius of the toroid.

Limitation of Ampere’s Circuital Law

The limitation of this law is that it is applicable in magnetostatics and is valid for the electric field does not change with time i.e. steady current. This is however overcome by using Maxwell modified Ampere’s law which introduces a displacement current.

Common Mistakes

Students can also go through the adoption of ampere circuit law to build a deeper understanding of the same. Not only is this exit part of ampere's law, but also as it is one of the basic concepts of physics and electricity.

Context and Applications

The main application is in calculating the magnetic field generated by an electric current. Ampere’s law has many applications in designing circuits, motors, transformers, generators, electromagnets, etc.

In each of the expert exams for undergraduate and graduate publications, this topic is huge and is mainly used for:

• Bachelor of Technology in the Electrical and Electronic department
• Bachelor of Science in Physics
• Master of Science in Physics

Related Concepts

• Gauss's law 
• Biot-Savart law 

Practice Problems

Q1. What is the magnetic field inside a pipe?

(a) Unity

(b) Infinity

(c) Zero

(d) Two

Correct option: (c)

Explanation: The magnetic field inside a hollow cylindrical wire is zero. A pipe can be considered a hollow cylinder. Hence, the magnetic field inside a pipe is zero. 

Q2. Which law can ampere’s circuital be derived from?

(a) Maxwell’s law

(b) Gauss law

(c) Kirchhoff’s law

(d) Biot-savart law

Correct option- (d)

Explanation: Biot-Savart's law gives the magnetic field produced due to a current carrying conductor. Both laws relate magnetic field to electric field. Hence, Ampere’s circuital law can be derived from the Biot-Savart law.

Q3. Ampere’s circuital law relates _________.

(a) electric field and charge

(b) magnetic field and current

(c) electric field and current

(d) none of these

Correct option- (b)

Explanation- Ampere’s Law can be stated as, “The magnetic field by an electric current is proportional to the size of that electric current". Hence, it relates magnetic field to electric current.

Q4. In Ampere's circuital law, what is the purpose of an 'Amperian Path'?

(a) Computation of magnetic field intensity

(b) Determination of differential

(c) Both

(d) None of these

Correct option: (a)

Explanation: Amperial circuit law uses the Amperian loop to locate the magnetic field in the area. 

Q5. Magnetic field at the center of a wire is

(a) Unity

(b) Zero

(c) Infinity

(d) None of these

Correct option: (b)

Explanation:

The expression for the magnetic field at a distance R from an infinite long straight wire is:

$B=\frac{{\mu }_{0}Ir}{2\mathrm{\pi }R}$

Here, $B$ is the strength of the magnetic field, $I$ is the current and $R$ is the radius and r is the distance from the center. If the distance from the center is zero, the magnetic field will be zero.