What is current division?
The method of the current division is extensively used in analyzing electric circuits. The current divider circuits are also known as parallel circuits. These are linear circuits that are used to split the current into branches that flow throughout the circuit. A current divider specially produces an output current which is a fraction of the total current (input current) that enters the circuit.
The primary job of a current divider is to split the current into different branches (also known as individual branch currents) of the divider so that the total energy expanded is minimum. Unlike the voltage divider, where the impedances of the voltage branches are placed on the numerator, the impedances of branch currents are placed in the denominator in the case of the current divider method. This makes the current follow a path of least impedance.
There are certain cases and conditions where the current divider rule can be applied, they are:
- The current divider rule can be applied when the components of a circuit are connected in parallel with the voltage or current source.
- The current divider rule can be applied to determine the individual branch currents, provided the total current and equivalent resistances are known.
- The current in any branch of the circuit is a fraction of the total current when two resistors are connected in parallel. If the individual resistance value of the two resistors is the same, the current gets divided equally throughout the circuit.
- In case, the circuit has three or more three parallel combinations of resistors, then the equivalent resistance parameter is used to divide the total current into branched currents.
In a current divider circuit, all the terminals of the components share the same end nodes resulting in different parallel paths and parallel branches. When the current flows through the circuit, they get divided into parallel branches. But, unlike voltage, the current associated with the branches are different. The values of individual branch currents are determined by Kirchhoff's current law (KCL), whereas the individual voltages are found out by Kirchhoff's voltage law (KVL).
The current divider formula
The generalized current divider formula is given by the following relation below,
where represents the current in the parallel circuit through the resistors
denotes the total current in the circuit
denotes equivalent resistance of the parallel circuit
denotes the resistive value of the resistors of the parallel circuit
The above current divider formula can also be expressed in terms of impedance and admittance. Hence, the current divider formula in terms of impedance is expressed as,
Where is the equivalent impedance value of the parallel circuit
represents the individual impedance values
The current divider formula in terms of the admittance values is given as,
where represents the equivalent admittance values
and, denotes the individual admittance values
Derivation of the current divider rule
In this section, a brief outline has been provided regarding the derivation of the current divider rule.
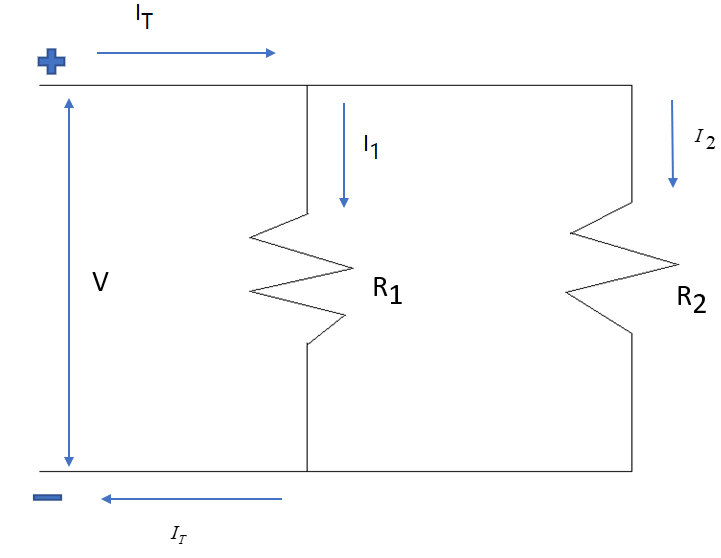
Consider the above circuit, which has a current source of voltage . The current from the voltage source is termed as the total current indicated by . The circuit consists of two resistors with resistances and connected in parallel. The current gets divided into and . The current flows through resistance and current flows through resistance . and recombine to give .
The total current in the circuit can be expressed as,
where
or,
Now, as the two resistors are connected in parallel, the equivalent resistance is given by,
From Ohm's law, it is known that , hence applying Ohm's law for resistor and current we get,
Similarly, applying Ohm's law for resistor R2 and current I2 we get,
Equating equations and we get,
Introducing the value of equation in equation , we get,
Introducing the value of equation in equation we get,
Which gives the current divider rule.
Parallel conductance
Apart from the current division method, the method of conductance can also be used to determine the current in the branched circuits. Conductance is the reciprocal of resistance in only DC circuits, and it is measured in Ohms.
Hence, for a circuit with several parallelly connected resistors, the conductance is simply the reciprocal of total resistances. It can be mathematically expressed as,
where, denotes the total resistance and and represent the individual resistance values.
If conductance is represented by then the above equation can be written as,
Context and Applications
The topic is taught in many undergraduate and postgraduate degree courses like:
- Bachelors of Technology (Electrical Engineering)
- Bachelors of Technology (Electronics Engineering)
- Bachelors of Technology (Electronics and Electrical Engineering)
- Bachelors of Technology (Mechanical Engineering)
- Masters of Technology (Electrical Engineering)
Practice Problems
Q1. Which of the following rule is used to determine the individual branched currents in a circuit?
a. Kirchhoff's current law
b. Thevenin's theorem
c. Theory of superposition
d. None of these
Answer: Option a
Explanation: Kirchhoff's current law or KCL denotes the total current entering and leaving the node of a circuit is equal to zero. Hence, KCl can be used to determine the individual branched currents in a circuit.
Q2. What is the reciprocal of resistance?
a. Impedance
b. Conductance
c. Capacitance
d. None of these
Answer: Option b
Explanation: Conductance is the reciprocal of resistance. Apart from the current division method, the method of conductance can be used to determine the individual currents in branched circuits.
Q3. What is the abbreviation of KVL?
a. Kirchhoff's volts law
b. Kirchhoff's voltage law
c. Klaus Keil voltage law
d. Klaus Keil volt law
Answer: Option b
Explanation: Kirchhoff's voltage law (KVL) is used to determine the individual voltages in a branched circuit.
Q4. What is the primary work of the current divider rule?
a. To divide the total current into individual branched currents
b. To divide the total resistance into individual resistances
c. Both a and b
d. None of these
Answer: Option a
Explanation: Current divider rule is used to determine the individual branched currents in a linear circuit. Essentially the components must be connected in parallel to apply the rule.
Q5. Which of the following is true in the current divider rule?
a. The energy is conserved
b. The impedance is conserved
c. The components must be connected in series
d. Total energy expanded should be minimum
Answer: Option d
Explanation: In a liner circuit the current divider rule is so applied that the total energy expanded remains minimum.
Want more help with your electrical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Electric Circuits and Networks
Circuit laws and method of analysis
Current division Method
Current Division Method Homework Questions from Fellow Students
Browse our recently answered Current Division Method homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.