What is the Fourier series?
Most of the incidents studied in the field of Engineering and Science as a function of time. For example, current and voltage are in the alternating current circuit. These occasional activities can be analyzed in the activity components (fundamental frequency and harmonics) through a process called Fourier analysis.
The Fourier series is an extension of the Fourier series that uses the orthogonal relationship between the sine and cosine functions.
What is the formula of Fourier series?
The formula of the Fourier series provides an extension of the function f(x). It is used to decrypt any periodic function activity or periodic signal into a set of simple oscillation functions, namely sine and cosine. Let’s understand the formula of the Fourier series using solved examples.
f(x)=12a0+∞∑ancosnxn=1+∞∑bnsinnxn=1
Here,
a0=1π∫π-πf(x)d
Fourier series square wave
A square wave is a non-sinusoidal periodic wave system in which the amplitude alternates at a constant frequency between a fixed and high base value, with the same minimum duration and amplitude. In an ideal square wave, the transition between the minimum and maximum is instantaneous.
A square wave is a special form of wave pulse that at least allows random duration and high amplitude. The average value time period is called the activity period. A true square wave has a 50% activity period (high and low multiples are equal integral).
Square waves are used as timepieces or "clock signals," because their rapid conversion is designed to activate sensitive circuits that correspond to precision timing. However, as shown in the frequency diagram, square waves contain various harmonics; they emit current or current pulses, disturb other nearby circuits, and generate noise or errors. To avoid this problem in highly sensitive circuits (such as accurate analog-to-digital converters), a sine wave is used instead of a square wave as a time indicator.
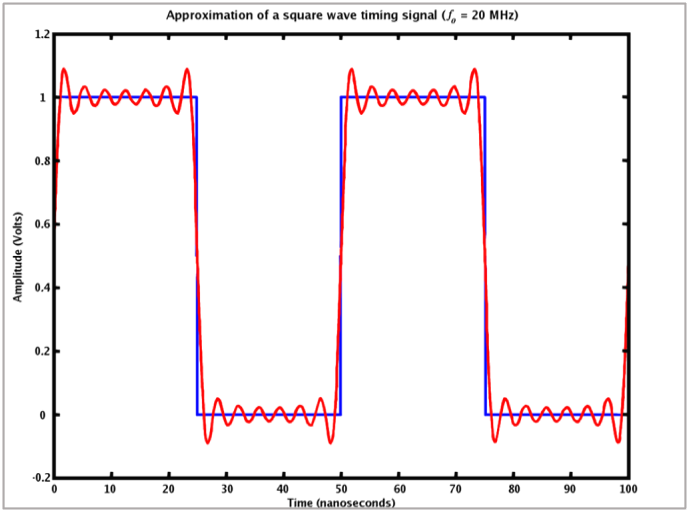
GNU Free Documentation License | https://commons.wikimedia.org | Matt Britt
Uses of the Fourier series
Fourier series, in mathematics, is an endless series used to solve special types of different mathematical equations. It contains an unlimited number of sines and cosines, and due to its periodicity (i.e., its double-digit values), it is a useful tool for analyzing periodic function activities.
Through the definition of the four-part sequence, it is known that the Fourier series can be defined as a method of expressing imaginary part work as a total (possibly infinite) function of sine and cosine wave functions. It is similar to the Taylor series, which represents an infinite number of monomial words and other functions.
Fourier integral theorem, these eigenfunctions in the “perfect” unity in relation to smooth and fully integrated functions over an infinite domain. The integral theory of compilation of the Fourier term series is simple and straightforward. Suppose f(x) slows down a bit and the Fourier series has an integral function that can be terminally integrated and the result is an infinitely flexible series that will combine into integral an interval f(x) combination. In the integral application of the Fourier inversion, the theory of the Fourier integral often plays an important role. In most cases the basic strategy is to use the Fourier transform, to do a specific task or to simplify, and then to apply the Fourier integral transform.
Gibbs phenomenon includes both the fact that the Fourier sums overshoot at jump discontinuity, and that this goes beyond
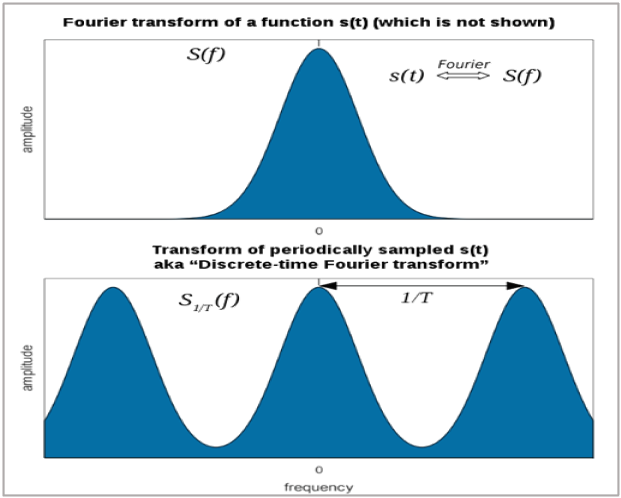
CC0 1.0 Universal Public Domain Dedication | https://commons.wikimedia.org | Bob K
Application of the Fourier series
The Fourier Series also has many applications for statistical analysis. Since it is a cosine block composed of many muscles at the same time, it is easy to separate and compress, which usually makes it easier to analyse functions such as sawtooth waves that are common in tests.
Discontinuous functions
The Fourier Series also offers a simplified analysis method for dealing with non-continuous tasks. The Dirichlet Theorem states the following:
If is the period , and if have the single value, it is limited. number of high and low numbers, and a finite number of non-proceedings, as well is finite, and the Fourier series converts to in all locations where continues on the jump, the Fourier series meets in the centre of the jump.
In other words, almost all jobs encountered in physics, whether continuous or discontinuous, can be represented by the Fourier analysis system
The Fourier analysis system can be used to analyze the phenomenon of physics either discontinuous or continuous. The Fourier series have more number of advantages than the Taylor series, one of these advantage is limitation on cohesion, which is the greatest Fourier series will do (for example, continue to request).
Generalized Fourier Series
The formula for Generalized Fourier Series:
Limitations of the Fourier series limitation
The essential limitation of the Fourier transform is that there is an inherent trade-off between frequency and time decisions. The duration of the Fourier transform used is very important to ensure subtle changes in frequency over the years, which is very important in bat echolocation calls and are visible.
Working of the Fourier series work
A Fourier series is a way of representing a periodic function as a (probable countless) sum of sine and cosine capabilities. For the ability of two variables that can be periodic function in each variable, the triangular basis in the Fourier series is changed by way of circular harmonics.
Common Mistakes
The important disadvantage of the Fourier transform is the inherent trade-off between frequency and time resolution. The length of the Fourier transform used is very important to ensure that subtle changes in frequency over the years can be seen, which is very important in bat echolocation calls.
Context and Applications
This subject matter is tremendous inside the expert exam for each undergraduate and graduate publication, mainly for:
- Bachelor of Technology in the mathematic
- Bachelor of Science in maths
- Master of Science in maths
Related Concepts
- Fourier transform
- Taylor series
- Binomial theorem
Practice Problems
Q1. Which of the subsequent isn't always Dirichlet’s condition for the Fourier series expansion?
- is periodic.
- has a finite number.
- has a limited range of maximum and minimum values.
- is periodic, single-valued, and finite.
Correct option: (d)
Explanation: Dirichlet’s situation for Fourier series expansion is ought to be periodic, single valued and finite; ought to have finite number of discontinuities in a single duration and should have finite range of maxima and minima in a period.
Q2. Find of the original function .
Correct option: (b)
Explanation:
Q3. The coefficients of the signal are carried from one position to another in Fourier series.
- True
- False
Correct option: (a)
Explanation: Yes, the coefficients of the signal are carried from one position to another. It is done for the simplification of the signal.
Q4. In case of discrete time signals, Fourier series is not true.
- True
- False
Correct Option: (b)
Explanation: If it follows the Dirichlet’s conditions, in case of discrete time signals, Fourier series is true.
Q5. Fourier coefficients is:
Correct option: (a)
Explanation: are all the coefficients of Fourier coefficients.
Want more help with your electrical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Signal and System
Fourier Analysis of Signal
Fourier Series of Signal
Fourier Series Homework Questions from Fellow Students
Browse our recently answered Fourier Series homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.