What is the gradient of a scalar field?
In vector calculus, the gradient of a scalar field f is always the vector field or vector-valued function . Its value at point p is the vector whose components are the partial derivatives of f at point p that is for , its gradient is defined at point p = in n-dimensional space.
The vector differential operators are denoted by the nabla symbol which is written as an upside-down triangle and is pronounced as "del". Direction and rate of fastest increase can be interpreted from the gradient vector. At a point p, if the gradient of a vector is non-zero, the direction of the gradient is in accordance with the direction in which the function increases most quickly from point p and the rate of increase in that direction is the magnitude of the gradient, that is the greatest absolute directional derivative. If the point is stationary then the gradient is the zero vector. In optimization theory, the gradient plays a major and fundamental role where, by gradient ascent, it is used to maximize a function. To the total derivative df, the gradient is dual. A vector at each point is the tangent vector. It is the value of the gradient at a point and a linear function on the vectors is a cotangent vector which is the value of the derivative at a point.
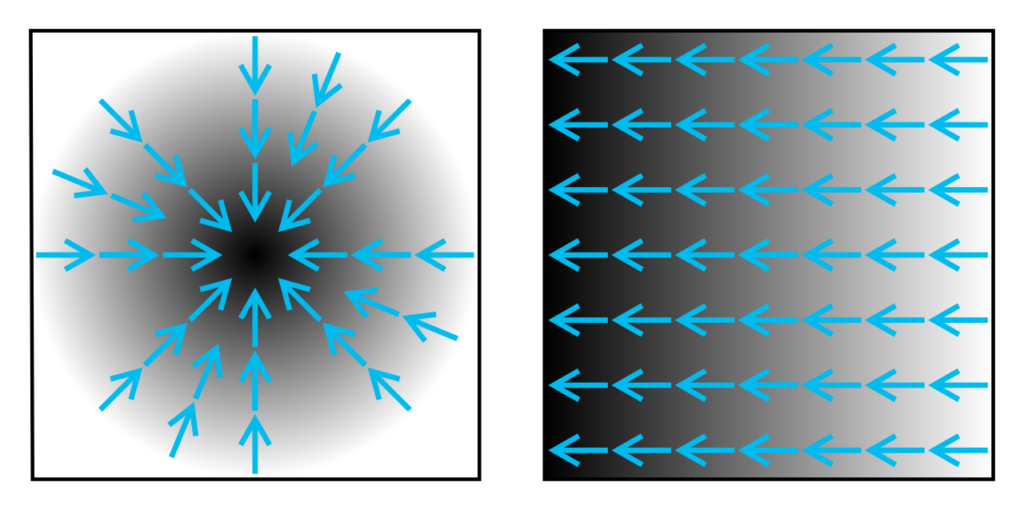
Motivation
Consider a room or a place where the temperature is denoted by a scalar field T, such that at each point (x, y, z), the temperature is given as T(x, y, z). It is independent of time, in which the temperature rises most quickly. The gradient of T will show the direction at that point by moving away from (x, y, z). How far will the rise in temperature in that direction be determined by the gradient magnitude? Consider a surface that has a height above sea level at point (x, y) which is given by H(x, y). At that point, pointing in the direction of the steepest slope or grade is the gradient of H. The magnitude of the gradient of the vector gives the steepness of the slope at that point. How a scalar field changes in another direction can be measured by the gradient by taking a dot product rather than just the direction of the greatest change?
Notation
The gradient of a function f at point p is written usually as . By any of the following it can also be denoted:
- : To emphasize the vector nature of the result
- grad f
- : Einstein notation
Definition
The gradient or the gradient vector field of a scalar field function is given by
where the symbol stands for vector differential operator, del.
To represent the gradient, the notation grad f is commonly used. The grad f is defined as the vector field whose dot product with any kind of vector v at each point of x is the directional derivative of f along with vector v which is given by
.
The gradient often refers simply to the vector of its spatial derivatives only when a function depends on a parameter such as time. Of the particular coordinate representation, the magnitude and direction of the gradient vector are independent.
Cartesian coordinates
The gradient in the three-dimensional cartesian coordinate system is given by,
where, i, j and k = standard unit vectors along with the direction of x, y, and z coordinates.
In a rectangular coordinate system, it is required to represent the gradient as a row vector or column vector of its components.
Cylindrical and Spherical coordinates
The gradient in the cylindrical coordinates with a Euclidean metric is given by,
=
where, = axial distance, = azimuthal or azimuth angle and z = axial coordinate and = unit vectors pointing along with the coordinates.
The gradient in spherical coordinates is given by,
where r= radial distance, =azimuth angle and = polar angle and = local unit vectors pointing in the coordinate direction.
General coordinates
General coordinates are written as
where n is the number of dimensions of the domain. In the list of the coordinate or component, the upper index refers to the position, hence, refers to the second component, not the quantity x squared. The arbitrary element is referred to as index variable i. The gradient can be written using Einstein notation :
and its dual is
where are used to refer to the unnormalized local covariant and bases of covariant, = inverse matric tensor.
We can easily express the gradient if the coordinates are orthogonal in terms of the normalized base using the scale factors known as Lame coefficients -
:
( and, )
where
Since it is not possible to avoid the repetition of more than two indices. We cannot use Einstein notation.
Properties and Applications
Level sets
Where some functions have a given value, a level surface or isosurface is the set of all points. If the function f is differentiable, then at a point x the dot product of of the gradient gives the directional derivative of function f at point x in the direction of v. To the level sets of f, the gradient of f is orthogonal. Such that dF is nowhere zero, any embedded hypersurface can be cut out with an equation of the type of . To the hypersurface, the gradient is then normal.
Conservative vector field and the gradient
A gradient field is the gradient of a function. A conservative vector field is the gradient of a vector field and only on the endpoints of the path does its line integral depends and is evaluated with the help of gradient theorem. A gradient of a function is the conservative vector field in a converse way.
Context and Applications
This topic is significant in the professional exam for undergraduate, graduate, and postgraduate courses:
- Bachelors of Technology in Electrical Engineering
- Masters of Technology in Electrical Engineering
Practice Problems
Question 1: What is the other name of the del operator?
- Divergence operator
- Gradient operator
- Curl operator
- Laplacian operator
Answer: Option b
Explanation: The vector Gradient operator is denoted by the symbol nabla (∇). It is written as an upside-down triangle and is pronounced as "del".
Question 2: Where is the gradient taken?
- tensor
- vector
- scalar
- anything
Answer: Option c
Explanation: Only on scalar filed the gradient is taken and after taking the gradient the scalar field becomes a vector field.
Question 3: How can electric field E be written?
- -gradient of V
- -Laplacian of V
- Gradient of V
- Laplacian of V
Answer: Option a
Explanation: In the direction of increase of the electric field, the potential difference decreases so the electric field is nothing but only the negative of the gradient of potential difference.
Question 4: Is the gradient of a function is constant?
- Yes
- No
- Maybe
- Cannot be determined
Answer: Option b
Explanation: The gradient of any scalar function is a vector function and so it is not constant because it changes its direction and magnitude with time.
Question 5: What is equivalent to the divergence of the gradient of a vector function?
- Laplacian operation
- Curl operation
- Double gradient operation
- Null vector
Answer: Option a
Explanation: Div (Grad V) = which is called the Laplacian operation
Related concepts
- Curl
- Divergence
- Four-gradient
- Hessian matrix
- Skew gradient
Want more help with your electrical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Electromagnetic field theory
Vector calculus
Gradient of scalar field
Gradient of a Scalar Field Homework Questions from Fellow Students
Browse our recently answered Gradient of a Scalar Field homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.