What is wave propagation?

Any of the ways how waves travel is known as wave propagation. One can find the difference between longitudinal wave and transverse wave with respect to the direction of oscillation, which is related to the propagation direction. Propagation may occur in vacuum for electromagnetic waves as well as in material medium. Other types of waves need a transmission medium to exist and cannot propagate through the vacuum. The amplitude of a wave is the maximum distance from the displacement of the particle from its resting position on the medium. The waves that propagate are of two types, Pressure waves or Shear waves.

Plane wave

A special case of wave or field is the plane wave in physics. It is a type of physical quantity whose value is constant over any plane and is orthogonal to a fixed direction in space. The value of such field for any position $\overrightarrow{x}$ in space and time t is given by, 

$F(\overrightarrow{x}, t) = G(\overrightarrow{x}. \overrightarrow{n}, t)$

where $\overrightarrow{n}$ = unit length vector

G(d, t) is a function that provides a field value from only two types of real parameters: the time t and $d = \overrightarrow{x}.\overrightarrow{n}$, where d is the scalar-valued displacement of the point $\overrightarrow{x}$ along the direction of $\overrightarrow{n}$. Perpendicular to $\overrightarrow{n}$, the displacement is constant over each plane. The field F may have values that are scalars, vectors, or any other physical/mathematical quantity. As in a complex exponential plane wave, they can be complex numbers. If the vectors are always co-linear with the vector $\overrightarrow{n}$, it is known as longitudinal wave and if they are always perpendicular to it then it is known as a transverse wave.

Special types

Traveling plane wave

A plane wave is referred to as a traveling plane wave. At a constant wave speed, the evolution of traveling plane waves can be described as a simple translation of the field along the direction, orthogonal to the wave fronts. This field can be written as,

$F\left(\overrightarrow{x,}t\right) = G(\overrightarrow{x}. \overrightarrow{n}-ct)$

where G(u) is the function of a single real component, u = d-ct, and it describes the wave profile, namely the value of the field at t = 0 for each displacement $d = \overrightarrow{x}.\overrightarrow{n}$. Here, $\overrightarrow{n}$ denotes the direction of propagation. A wavefront is defined as the moving plane which is perpendicular to $\overrightarrow{n}$ at a distance of d+ct from the origin for each displacement d. With velocity c, the plane travels along the direction of propagation $\overrightarrow{n}$. At every one of its points, the value of the field is the same and constant with time.

Sinusoidal plane wave

The term sinusoidal plane wave also means "monochromatic" and is a type of traveling plane wave whose profile G(u) is a sinusoidal function, which is given by,

$F(\overrightarrow{x}, t) = A \sin (2\mathrm{\pi f}(\overrightarrow{x}. \overrightarrow{n} - \mathrm{ct}) + \psi )$

where A = amplitude of the wave which is a scalar or a vector

f = spatial frequency 

$\psi$ = phase

Since the true plane wave has to fill all the space, it cannot exist physically. In physics, the plane wave model is important and is widely used. The waves emitted by any source with finite extent into a large homogeneous region of space can be well approximated by plane waves when viewed over any part of that region that is sufficiently small compared to its distance from the source. 

Plane standing wave

A standing wave is a field whose value can be expressed as the product of two functions, one dependent only on position and the other dependent only on time. A plane standing wave, in particular, can be expressed as, 

$F(\overrightarrow{x}, t) = G(\overrightarrow{x}. \overrightarrow{n}) S\left(t\right)$

where G = function of one scalar parameter with scalar or vector values

S = scalar function of time

This representation is not unique, since the same field values are obtained if S and G are scaled by reciprocal factors. 

Properties of plane wave

By ignoring the directions perpendicular to the direction of the vector $\overrightarrow{n}$, a plane wave can be studied. Like a wave in a one-directional medium, it can be done by considering the function $G(z, t) = F(z\overrightarrow{n}, t)$. A plane wave is yielded when any local operator, linear or non-linear, is applied to a plane wave. With the same normal vector $\overrightarrow{n}$, any normal linear combination of plane waves is also a plane wave. The gradient of the field is always co-linear with the direction $\overrightarrow{n}$ for a scalar plane wave in two or three dimensions which is given specifically by the equation $\nabla F(\overrightarrow{x}, t) = \overrightarrow{n} {\partial }_{1}G(\overrightarrow{x}. \overrightarrow{n}, t)$ where ${\partial }_{1}G$ = partial derivative of G with respect to the first argument.

The vector-valued plane wave's divergence depends only on the projection of the vector G(d, t) in the direction towards $\overrightarrow{n}$ and is given specifically by,

$(\nabla .F)(\overrightarrow{x}, t) = \overrightarrow{n}. {\partial }_{1}G (\overrightarrow{x}. \overrightarrow{n}, t)$

A transverse planar wave must particularly satisfy $\nabla .F = 0$ for all $\overrightarrow{x}$ and t. For a plane wave, the amplitude is constant that is the wave does not attenuate.

Plane wave expansion

A plane wave expansion in physics is expressed as a linear combination of a spherical type of waves and is given by the equation,

$e^{ik.r} = \sum _{t=0}^{\infty } (2l + 1) i^l{j}_l\left(kr\right) P_{L }(\hat{k}. \hat{r})$

where, i = imaginary unit

k= wave vector 

r = position vector

$j_l$ = spherical Bessel functions

$P_l$ = Legendre polynomials

Wave equation and wave number

A second-order linear partial differential equation, which is used for describing a wave is called the wave equation. It is also known as the two-way wave equation because the second-order wave equation describes only the superposition of both incoming and outgoing waves.

The spatial frequency of the wave is called wave number. It is measured in cycles per unit distance/radians per unit distance. The number of waves per unit distance is called the wave number.

Plane electromagnetic waves

The existence of a combined electric field and a magnetic field is the most significant prediction of Maxwell's equation that propagates as electromagnetic waves through space. The electric field is the force per unit stationary charge and the magnetic field is the force per unit moving charge. According to Gauss' law of electric field, an electric field implies the relative directions and the propagational directions of an electromagnetic wave.

Context and Applications

This topic is significant in the professional exam for Under-graduate, Graduate, and Postgraduate courses:

• Bachelors in Electrical Engineering
• Bachelors in Electronics and Telecommunication
• Masters in Electrical Engineering
• Masters in Electronics and Telecommunication

Practice Problems

1. What is the minimum  angle between electric  field and magnetic field vectors, for a plane wave propagation?

1. 0 degree
2. 60 degree
3. 90 degree
4. 180 degree

Answer- c

Explanation: The angle between electric field and magnetic field for a plane wave propagation in an unbounded medium is always 90 degrees.

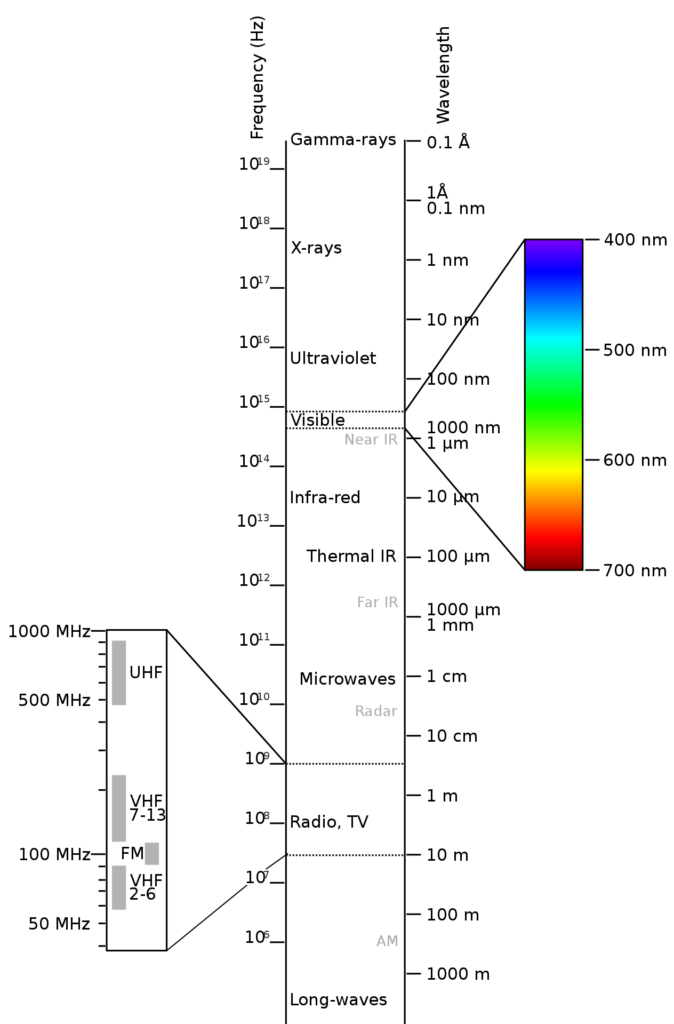
2. Which of the following rays has the lowest frequency?

1. X-RAYS
2. UV RAYS
3. Gamma rays
4. Visible light

Answer- d

Explanation: Under the spectrum of electromagnetic plane ways, visible light has the lowest frequency among the given options.

3. In which medium, the propagation of electromagnetic waves can take place?

1. Vacuum
2. Material medium
3. Both a and b
4. None of these

Answer- c

Explanation: Propagation may occur in a vacuum for electromagnetic waves as well as in a material medium.

4. What are the two types of waves that propagate?

1. Pressure waves
2. Shear waves
3. Both a and b
4. None of these

Answer- c

Explanation: The waves that propagate are of two types, Pressure waves or Shear waves.

5. Which type of differential equation is used in the wave equation?

1. First-order differential equation
2. Second-order differential equation
3. Both 1 and 2
4. None of these

Answer- b

Explanation: A second-order linear partial differential equation is used for the description of waves which is called the wave equation

Related Concepts

• Plane wave expansion
• Rectilinear propagation
• Wave equation
• Weyl expansion