What is polar and exponential representation?
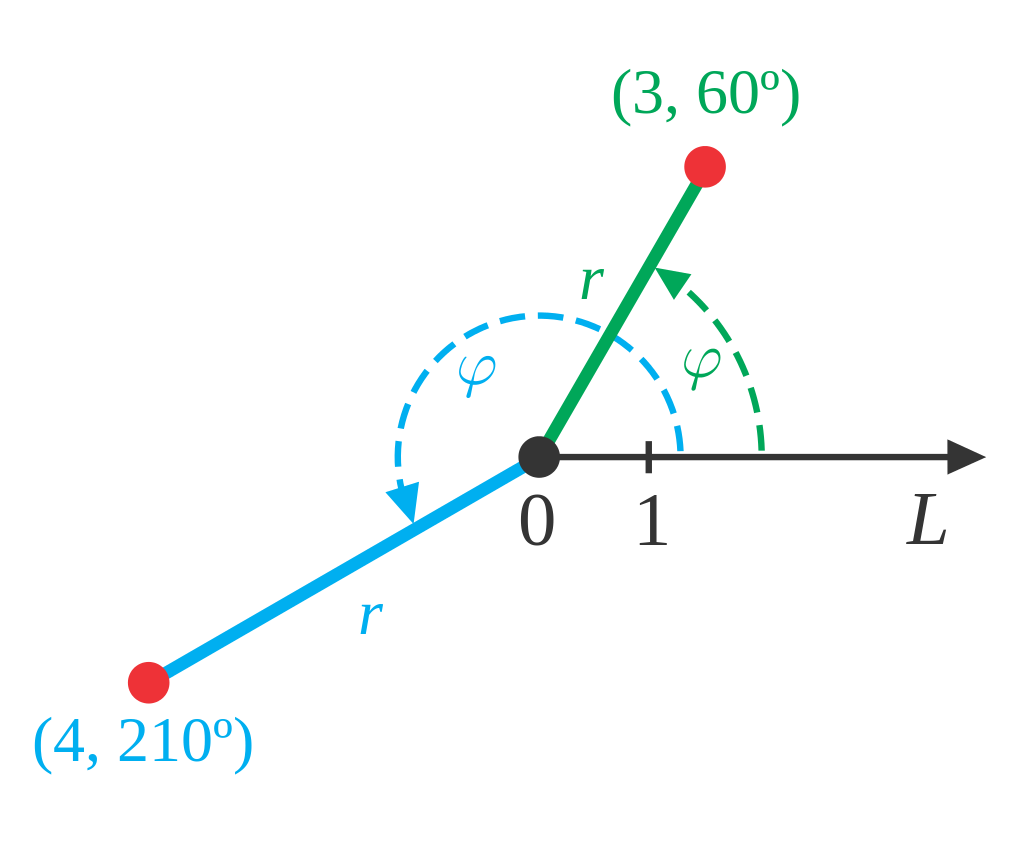
The polar form of a complex number is written according to its size and angle. Therefore, the vector of the polar form is presented as , where Z is a complex number in the form of a polar, A is a magnitude or modular vector and is an angle or a collision that can be either good or bad. The size and angle of the point remain the same as the rectangular form above. In this case, the polar state of the point is represented by the "triangular form".
Since the polar representation of a point is based on a triangular form, we can use the simple geometry of the triangle and especially the trigonometry and Pythagoras theorem of the triangle to determine both size and complex number angles. As we recall in school, trigonometry refers to the relationship between sides and triangular angles so that we can define relationships between sides.
The Exponential Form uses your trigonometric functions of both the sine (sin) and cosine (cos) triangular values to define the complex exponential as the orbits of a complex plane. The interpreter's form for obtaining a point is based on Euler's Identity, named after Swiss mathematician Leonhard Euler and is provided by:
Euler's identity is very similar to the polar form above and shows us that a number similar to with size 1 is also a complex number. We can not only convert complex numbers in exposure form into a polar form such as but Euler's identity also gives us a way to convert a complex number from its descriptive type into its rectangular shape. Then there is the relationship between the exponential, polar, and rectangular forms in defining complex numbers.
Complex number representation
The complex number then consists of two distinct but closely related parts, a “Real Number” and a “Symbolic Number” or "imaginary number".
Complex numbers represent points in a complex area of two sizes or planes referring to two different axes. A horizontal axis is called a real axis while a vertical axis is called an imaginary axis. The real and imaginary parts of a complex number are abbreviated as Re (z) and Im (z), respectively.
Complex numbers made up of actual (active component) and imaginary numbers (active component) numbers can be added, subtracted, and used exactly the same as the first algebra used to analyze DC Circuits.
The rules and regulations used in mathematics for the addition or subtraction of hypothetical numbers are the same as for real numbers, etc. The only difference is in the multiplication because the two hypothetical numbers multiply together into a real negative number. Real numbers can also be thought of as complex numbers but with a zero number marked .
The j-operator has a value equal to so a sequential repetition of will result in j having the following values, -1, -j, and +1. Since the j-operator is commonly used to indicate a vector clock rotation, each successive repetition or power and so on, will force the vector to rotate at a constant angle of 90o toward the opposite angle.
Multiplication and division using polar form
Multiplication in polar form
The rectangular form is best for adding and subtracting complex numbers as we have seen above, but the polar state is generally better for duplication and division. In order to double together two vectors in polar form, we must first duplicate two or more modulus and then combine their angles.
Where Z1, Z2 are vectors with A1and A2 as their lengths or magnitude and θ1, θ2 as their angles with respect to the x-axis.
Multiplying and in polar form gives us .
Division polar form
To divide or separate two vectors in the polar state, we must separate the two moduli and subtract their angles.
Where Z1, Z2 are vectors with A1and A2 as their lengths or magnitude and θ1, θ2 as their angles with respect to the x-axis.
Fortunately, modern science calculators are built into mathematical operations that allow for easy transformation of rectangular form into a cooler, (R → P) and from a cooler, rectangular (R → P).
Phasor notation
Different ways of representing a rotating vector or vertical vector using complex numbers to define a point in a complex plane. Phasor notation is the process of constructing a single complex number with a length and a phase angle of a given sinusoidal waveform.
Then the phasor notation or phasor converts as it is sometimes called, transferring the real part of the sinusoidal function:
Context and Applications
This topic is important for professional exams in both undergraduate and postgraduate studies and in particular:
- Bachelors in Electrical Engineering
- Masters in Electrical Engineering
Practice Problems
Q1. Which of the following forms is used for multiplication and division of phasor?
- Rectangular form
- Polar form
- Both of the above
- None of the above
Answer: Option b
Explanation: Polar form is used for multiplication and division of phasor because it multiplies or divides just values and adds or subtracts the angles.
Q2. In which of the following forms, the length and the angle of a vector are represented?
- Rectangular
- Exponential
- Polar
- None of the above
Answer: Option c
Explanation: In the polar form of phasor in the AC circuit, the length and the angle of a vector are represented.
Q3. In which of the following forms is the Φ an angle with reference to the axis?
- Exponential
- Polar
- Rectangular
- None of the above
Answer: Option a
Explanation: In the exponential form of representation, the angle Φ is measured with respect to the axis.
Q4. Which of the following is used as a vector to represent a sinusoidal signal?
- Amplitude
- Phasor
- Both a and b
- None of the above
Answer: Option b
Explanation: Phasor is a vector used to represent a sinusoidal signal.
Q5. According to the international standards phasor always rotates in which of the following directions?
- Clockwise
- Counter-clockwise
- Both a and b
- None of the above
Answer: Option b
Explanation: According to international standards, the Phasor always rotates in an anticlockwise direction.
Want more help with your electrical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Electric Circuits and Networks
Complex form Representation
Polar and exponential representation
Polar and exponential representation Homework Questions from Fellow Students
Browse our recently answered Polar and exponential representation homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.