What is power flow analysis?
Power flow analysis is a topic in power engineering. It is the flow of electric power in a system. The power flow analysis is preliminary used for the various components of Alternating Current (AC) power, such as the voltage, current, real power, reactive power, and voltage angles under given load conditions and is often known as a load flow study or load flow analysis.
The necessity of power flow analysis
The power flow analysis or load flow analysis is extensively used in the operations and planning of power systems. The power systems need to be planned, designed, and maintained by the engineers to ensure that the power systems should operate properly within safe limits. The power flow study is also necessary so that the power system should sufficiently deliver the required power all the time despite the fluctuations and contingencies. The power flow study is also necessary to design the equipment necessary for the power systems, placement of the reactive power compensation, and optimization of transformer taps in a power system. The power flow study is necessary for the planning of the expansion of the power system and also for analyzing the best operations of the existing systems. The load flow study is usually done for the systems having multiple load centers, for example in the commercial power systems. The power flow analysis on the existing system is useful for identifying the total system losses and individual losses, and obtaining information about the maximum capacity of flow transferred by a system, and minimizing the operational costs. The results of such analysis are obtained in the terms of active power, reactive power, phase angle, and voltage magnitudes.
Problem Formation of Power flow analysis
The motive of analyzing the power flow is, to get the complete details about the angle and magnitude of voltages of each bus in a power system. It also gives details of specified voltage magnitude, load, and generator power conditions. After all the data is obtained, the generator reactive power and real and reactive power of each branch are determined by analyzing the system analytically. The known and unknown variables of the system are identified first before performing the power flow analysis. The type of variables depends upon the type of bus. There are two types of buses in a system: The load bus and the generator bus. The load bus, also known as the P-Q bus, is the bus that does not contain any generator. In a load bus, real and reactive powers are specified but the voltage magnitude and voltage phase angles are unknown. The generator bus or the P-V bus is the bus that contains at least one generator. The real power and voltage magnitude are known, and the reactive power and voltage phase angles are unknown. There are four variables associated with each bus:
- Active power (P)
- Reactive power (Q)
- Voltage magnitude (|V|)
- Voltage phase angle
The basic equation for the power-flow analysis is obtained from the nodal analysis. While generating the equation for power flow, it is assumed that the real power and reactive power at each load bus are predetermined. The real power is denoted by PD and the reactive power is denoted by QD. For the generator bus, it is assumed that the real power generated (PG) and the voltage magnitude |V| is known. After all the data is obtained, the real and reactive power balance equations are obtained for the load bus and the real power balance equation is obtained for the generator bus. The equations obtained contain the bus admittance matrix and are solved by using various methods.
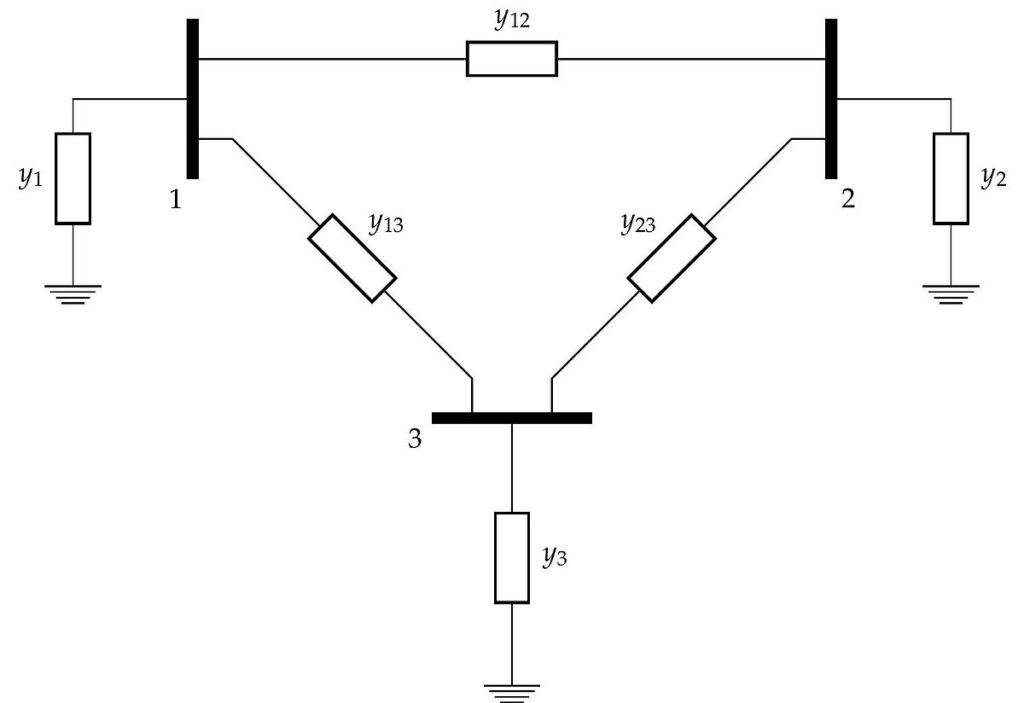
Methods to solve power flow equations
The equations obtained in the power flow analysis are non-linear and there are different methods used for solving them. The equations are solved for determining the voltage magnitude and voltage angles at each busbar unless the equilibrium is obtained in the active and reactive power. The various manual methods used for solving the power flow equations to obtain the optimal power flow are- Newton-Raphson method, Gauss-Seidel method, and Fast-Decoupled power flow method. The solutions are also obtained using various state-of-the-art software such as CYME, DINIS, ETAP, IPSA, and so on.
Newton-Raphson method
The Newton-Raphson method is an iterative method used for finding the roots of non-linear equations. For the power flow or load flow analysis, the first-order Newton-Raphson equation is obtained. First, an initial guess of the solution is made. In common practice, initially, the voltage angle is assumed as zero, and voltage magnitude is assumed as 1. Then the iterations are done by considering the most recent voltage angle and voltage magnitude values. The disadvantages of this method are that the iterations take much longer time to calculate and the solution is always approximate solution, not an exact solution.
Gauss-Seidel method
Gauss-Seidel method is also an iterative method used for finding the solutions of non-linear equations. This method is used to solve iterations faster. But the disadvantage of this method is that if the order of examining the equation is changed, the components of iteration are also changed.
Fast-Decoupled power flow method
The fast-decoupled power flow method is used for high voltage transmission systems. In high voltage transmission systems, a strong coupling is formed between the real power and voltage angle and also between reactive power and voltage magnitude. The weak coupling is formed between real power and voltage magnitude and also between reactive power and voltage angle. In the fast-decoupled power flow method, two steps are involved - decoupling the real and reactive power calculations and obtaining the matrix elements. Three assumptions are made while solving the equations using the fast-decoupled power flow method- conductance between buses is zero, the magnitude of the bus voltage is unity, that is the bus voltage is equal to one per unit, and sine of phases between the buses is zero. This method is an accurate method of obtaining the power flow solution and is used for real-time management of power grids on a large scale.
Context and Applications
The power flow analysis is taught in the following courses:
- Bachelors of Technology (Electrical Engineering)
- Masters of Technology (Power System and Power Electronics)
Practice Problems
1. What is another name for power flow analysis?
a) Load flow analysis
b) Current flow analysis
c) Electricity flow analysis
d) Resistor analysis
Answer- a
Explanation- Another name for the power flow analysis is load flow analysis.
2. Which of the following is not a variable associated with each bus?
a) Active power
b) Reactive power
c) Three-phase power
d) Voltage magnitude
Answer- c
Explanation- The three-phase power is not a variable associated with each bus.
3. Which of the following is not a manual method of solving the power flow equations?
a) Newton - Raphson method
b) Gauss - Seidel method
c) Switchgear analysis method
d) Fast-decoupled power flow method
Answer- c
Explanation- The switchgear analysis method is not a manual method of solving the power flow equations.
4. How many generators does a load bus contain?
a) zero
b) one
c) two
d) three
Answer- a
Explanation- A loaded bus contains no generator.
5. Which of the following is not a necessity of power flow analysis?
a) To plan the expansion of the power system
b) To design equipment necessary for the power system
c) To provide system-wide distribution of resistors
d) To analyze the best operations of the existing systems
Answer- c
Explanation- To provide system-wide distribution of resistors is not a necessity of power flow analysis.
Want more help with your electrical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Power Systems
Performance of Transmission line
Transmission line parameter
Power Flow Analysis Homework Questions from Fellow Students
Browse our recently answered Power Flow Analysis homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.