What is the trigonometric function?
Trigonometric functions are the functions that are periodic in nature, the trigonometric function are used to determine the relation between sides and the angles of a triangle. The major application of the trigonometric functions is in the right angled triangle.
What are the properties of trigonometric function?
The fundamental trigonometric function are named as sine, cosine, tangent, cotangent, secant, and cosecant function.
Two functions that are most important of all the functions are:
1- Sine function
2- Cosine function
Sine function
The sine function is one of the three major functions of a trigonometric function, and the other functions are the cosine and tangent functions. The sin x or sin theta can be defined as the ratio of the opposite face of a proper triangle to its hypotenuse in a right-angled triangle.
The sine characteristic is used to locate the unknown subtend angle or sides of a right triangle. The frequency of trigonometric function is the range of cycles in a sine or cosine curve with a given interval. This interval is typically sin 2π radians (or 360
The sine feature is an important interval in a trigonometric function. To understand the derivation of sine x, consider a unit circle focused at the origin of the y-x coordinate plane. Consider a variable factor on the boundary (circumference) of this circle. Examine that P is in the first quadrant, and OP makes an acute angle of x radians with the effective x-axis. PQ is the vertical line falling from P to the horizontal axis. Therefore, the triangle is formed by connecting the points O, P, and Q, as demonstrated in the determination.
The required sine function is: sin(x)=(QP)/(OP)
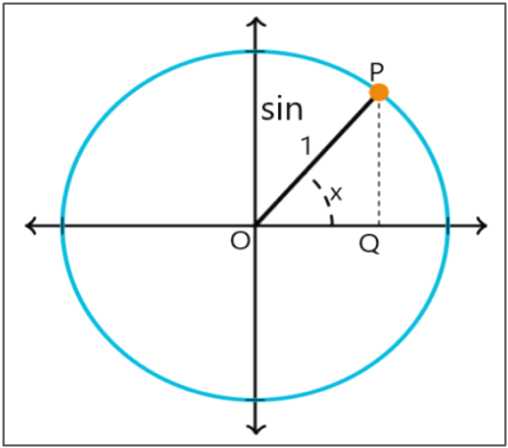
creative commons attribution-share alike 3.0 unported | https://commons.wikimedia.org/wiki/file:unit_circle_used_to_define_sine_and_cosine.svg | khan academy
Cosine function
The cosine function is one of the three major functions of a trigonometric function, and the other functions are the sine and tangent functions.
The cosine feature is one of the number one mathematical trigonometric functions. It's far defined in the context of a proper-angled triangle for acute angles. The cosine characteristic is used to model many real-existence eventualities – radio waves, tides, sound waves, musical tones, electric currents, etc.
The cosine function characteristic or cos x is an interval function in a trigonometric function. Consider a unit circle and a coordinate point on the circumference of the circle. A variable factor P moves on the circumference of this circle. From the figure, we have a look at that the point P that is in the first quadrant, and OP makes an acute perspective of x radians with the tremendous x-axis. PQ is the perpendicular dropped from p onto the horizontal y-axis. The triangle is thus formed by way of becoming a member of the points O, P, and Q as shown in the figure, in which OQ is the base, and PQ is the height of the triangle.
The required cosine function is: cos(x)=(OQ)/(OP)
The sine function graph and quadrants
Before getting to the graph of the sine feature, Consider how the values of sin x vary on a unit circle, then plot them on the graph. As shown in the picture above, notice that sin x = PQ/OP = PQ/1 = PQ. As x varies, the value of sin x varies with the variation in the length of PQ. Now, consider the variation inside the sine function inside the 4 quadrants of the coordinate plane.
The cosine function graph and quadrants
As shown in the figure above, notice that cos x = OQ/OP = OQ/1 = OQ. As x or (-x) varies, the fee of the cos x varies with the variation inside the duration of OQ. Now, observe the change of the cosine characteristic in the four quadrants of the coordinate plane.
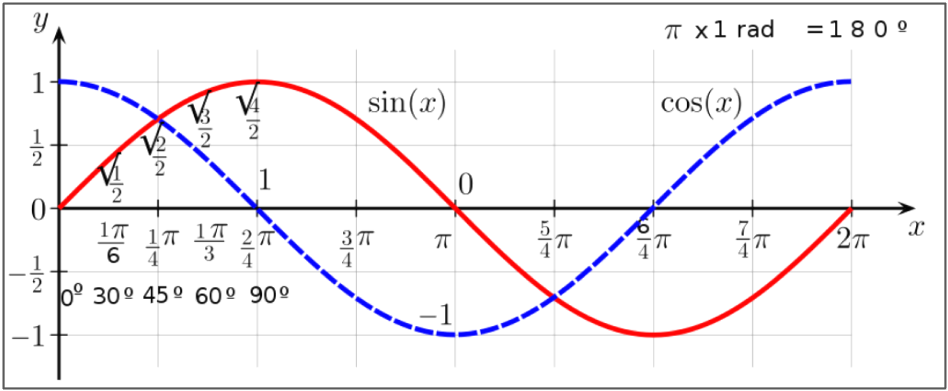
creative commons cc0 1.0 universal public domain dedication | https://commons.wikimedia.org/wiki/file:sine-cosine_function001.svg | pk0001
The inverse trigonometric function
Inverse trigonometric functions, as a subject of getting to know, are carefully associated with the primary trigonometric features. The domain and the range of the inverse trigonometric function are converted to the variety and domain of the inverse trigonometric capabilities.
The opposite trigonometric features have all the formulas of the basic trigonometric features, which include the total number of features, double and triple the inverse function. Consider the conversion of trigonometric formulas to the inverse function. The arc-sin function is the inverse of the sine function.
Some other trigonometric functions:
- Asymptote trigonometry
- Ptolemy trigonometry
Uses of trigonometric properties
- The calculus is based on trigonometric function and algebra.
- The essential trigonometric functions like sine and cosine are used to explain the sound and light waves.
- The trigonometric function is utilized in oceanography to calculate the heights of waves and tides in oceans.
- It is used within the advent of maps.
- It is miles utilized in satellite systems.
Real-life application of trigonometric properties
It may not be directly applied to solve sensitive problems, but it can be used in various fields. Consider that the trigonometric functions have application is aviation industry and in naval ships, they are used in radar technology as well as in the cartography.
Some basic formulas for sine and cosine function
If A+B=180° Then,
If Then,
If Then,
If Then,
Some basic trigonometric formulas
Various on the Pythagorean identity theorem:
Half angle formulas:
Double-angle formulas:
Law of sine:
Law of cosine:
Quotient identities:
Reciprocal identities:
Common Mistakes
Pay attention to the angle below and the opposite, adjacent sides, etc. If you want to take any angle value like then, take it carefully.
Context and Applications
In each of the expert exams for undergraduate and graduate publications, this topic is huge and is mainly used for:
- Bachelor of Technology in the electrical and electronic department
- Bachelor of Science Physics
- Master of Science Physics
Related Concepts
- Trigonometric Identity
- Trigonometric functions
Practice Problems
Q1. What is the value of ?
- 1
- 2
- 3
- 4
Correct option: (a)
Explanation: From the trignometric identities it is clear that the value of the given expression is 1.
Q2. What is the value of ?
Correct option: (b)
Explanation: According to the reciprocal identities the value of the given expression in the question is .
Q.3 If . Then the value of is:
Correct option: (b)
Explanation: According to the half angle formulas the value for the given expression in the question is .
Q4. The value of and are:
- same
- different
- same but negative
- none of these
Correct option: (a)
Explanation: The value of both the functions is same as .
Q5. What is the value of ?
- None of these
Correct option: (c)
Explanation: As we know that the value of and .
Want more help with your electrical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Property of trigonometry function Homework Questions from Fellow Students
Browse our recently answered Property of trigonometry function homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.