What is a Vector field?

In Physics and Mathematics vector calculus attached to each point in a subset of space, there is an assignment of a vector in a field called a vector field.

For instance, each field attached to a point in the plane, the vector field can be assumed or visualized as a collection of arrows with a given direction and magnitude. These vector fields are used to model. For instance, the strength and direction of some forces such as gravitational force or magnetic force which changes from one point to another point or throughout the space. The elements of integral calculus and differential calculus are extended naturally to a vector field. The line integral of the vector field gives us the work done by a force that is moving along a path when the vector field represents force. As a special case of the fundamental theorem of calculus, conservation of energy is exhibited under this interpretation. In space, the vector fields are representing the velocity of the moving flow and the physical intuition leads to terms such as "curl" which represents the rotation of the flow, and "divergence" which represents the rate of change of volume of the flow. Del or nabla is an operator which is used in mathematics particularly in vector calculus as a "vector differential operator". It is represented by the nabla symbol $\nabla$. Vector fields are defined as differentiable manifolds which are spaces.  

Field lines of a vector field

Let U be an open subset of $R^n$. A function of F is a vector field on U. Attached to points of U, represented by arrows, a vector field F can be realized on an open set $U\subset R^3$ as a "field of vectors". The length of the vector gives the strength of the field at a point. The direction of the field is given by the arrow as shown in the diagram. The vector field evaluated at a point P (say) is the tangent to the curve through P. These curve lines are known as the field lines of the vector field. Always following the direction of the field, the field lines are threading their ways through the vector field. The field lines are simply the paths of the fluid particle in the case of the velocity field of the fluid.

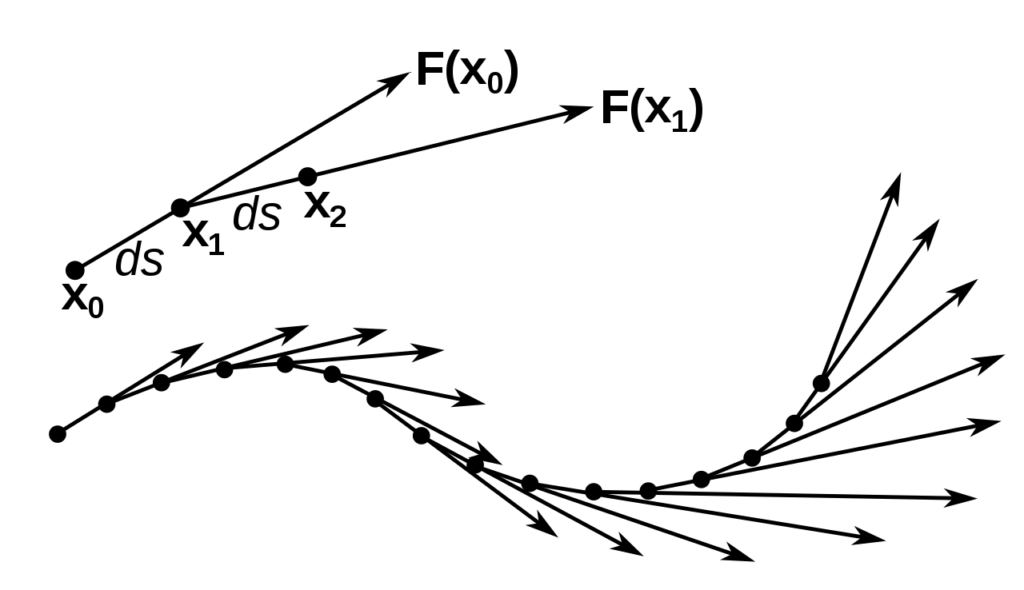
Types of vector fields

There are two types of vector fields:

1. Lamellar, irrotational, or conservative vector field
2. Solenoidal rotational or non-conservative vector field

Lamellar, irrotational, or conservative vector field

The field that is the gradient of some function is called a lamellar, irrotational, or conservative vector field in vector calculus. The line strength is not dependent on the path in these kinds of fields. The value of the line integral is not changed with the choice of any path between two points. In three dimensions, the conservative vector field has a vanishing curl that is, this field is irrotational. Provided that the domain is simply connected, an irrotational vector field is necessarily conservative.

Let n = 3 and v: $U\to R^3$ be a $C^1$ vector field with U open.

Then v is called irrotational if its curl is zero that is, $\nabla \times v = 0$.

Due to this reason, such types of vector fields are generally called curl-free vector fields or curl-less vector fields. Also, they are called longitudinal vector fields. For any $C^2$ scalar field $\psi$ on U, we have $\nabla \times (\nabla \psi ) \equiv 0$. So this implies that every $C^1$ vector field on U is also an irrotational field on U. The converse is also true, provided that the U is simply connected, that is, every irrotational field on U is a $C^1$ conservative vector field on U. If U is not simply connected, then in general the above statement is not true. If this is true then v has curl equal to zero everywhere in U, that is, v is irrotational. 

An irrotational vector field has path independence property in a simply connected open region. In such types of regions, the irrotational vector field is conservative and these fields have path independent properties. By using Stoke's theorem, the result can also be proved directly.

Solenoidal vector field

In the mathematics of vector calculus, a solenoidal vector field is also known as a divergence-free vector field, an incompressible vector field, or a transverse vector field. It is a type of transverse vector field v with divergence equal to zero at all of the points in the field, that is $\nabla ·v = 0$. It can be said that the field has no source or sink and this is the common way to express it. The zero divergence is the type of test to determine if a given field is solenoidal or not.

Properties of a solenoidal vector field

An integral definition of a solenoidal field is given by the divergence theorem. The net total flux must be zero for any closed surface, that is : $∯ v . dS = 0$

where, $dS$= outward normal to each surface element. 

According to the fundamental theorem of vector calculus, any vector field can be written or expressed as the sum of a solenoidal field and an irrotational field. Whenever a vector field v has a vector potential component, the condition of zero divergence is satisfied because the definition of vector potential A is given by, $v = \nabla \times A$ which automatically results in an identity function as can be shown. For instance, using cartesian coordinates, that is $\nabla ·v = \nabla ·(\nabla \times A) = 0$The converse is also true that is for any solenoidal field v, a vector potential A exists such that $v = \nabla \times A$.

Some examples of solenoidal fields are:

• The magnetic field B.
• The velocity field of an incompressible flow of fluid.
• The vorticity field.
• In neutral regions, the electric field E where ${\rho }_e = 0$.
• The current density J where $\frac{\partial {\rho }_e}{\partial t} = 0$ which means the charge density is unvarying.
• The magnetic vector potential A (Coulomb gauge).

Context and Applications

This topic is significant in the professional  exam for undergraduate, graduate, and postgraduate courses:

• Bachelors of Technology (Electrical Engineering)
• Masters of Technology (Electrical Engineering)

Practice Problems

Question 1: What is $\overrightarrow{V}$ called when div $\overrightarrow{V} = 0$?

1. Rotational
2. solenoidal
3. irrotational
4. none of the above

Correct option: b

Explanation: A vector function $\overrightarrow{V}$ is defined as a solenoidal vector if $\nabla ·\overrightarrow{V } = 0$.

Question 2: What is the divergence of a continuous vector function which is twice differentiable?

1. unity
2. infinity
3. zero
4. a unit vector

Correct option: c

Explanation: The second derivatives are independent of the order in which the derivatives are applied if the function is twice continuously differentiable. In the expression for curl, all the terms are canceled.

Question 3 : Which are the solenoidal fields among the given options?

1. The magnetic field B
2. The vorticity field
3. The current density J
4. All of the above

Answer: Correct option 4

Explanation: The example of solenoidal fields are magnetic field B, vorticity field, the current density J, etc.

Question 4: Which operator is used as a vector differential operator?

1. $\nabla$
2. $∆$
3. $\partial$
4. $\varnothing$

Correct option: a

Explanation : Del or nabla is an operator which is used in mathematics particularly in vector calculus as a "vector differential operator". It is represented by the nabla symbol $\nabla$.

Question 5: What does the line integral of a vector field give us?

1. Potential difference
2. Work done
3. Force
4. Torque

Correct option : b

Explanation: The line integral of the vector field gives us the work done by a force that is moving along a path when the vector field represents force.

Related Concepts

• Longitudinal and transverse vector field
• Stream function
• Conservative vector field