What is a spherical coordinate system?

The spherical coordinate system is a three-dimensional coordinate system for space where the position of a point is specified by three numbers- the radial distance of that point from a fixed source, its polar angle measured from a certain zenith, and the azimuth angle. Its orthogonal projection on the reference plane passes through the source and is measured from the direction of constant reference on that plane which is orthogonal to the highest level. It can be viewed as a three-dimensional version of the polar coordinate system.

The spherical coordinate system normalizes to the two-dimensional polar coordinate system. It also extends to high-dimensional spaces and is later referred to as the hyper spiral coordinate system.

The spherical coordinate system is defined in relation to the Cartesian system. The circulatory system uses the distance measured from the source (r) and the angle measured from the +z-axis to the plane z = 0.

The angle ($\varphi$) is measured in the plane of constant z as in a cylindrical system.

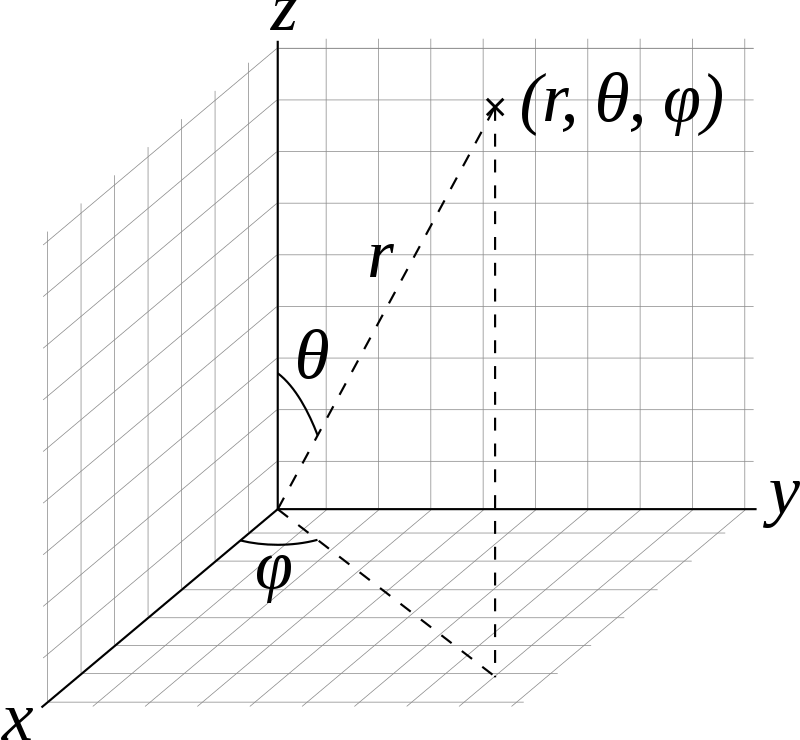
Spherical coordinates are preferred when the geometry of the problem exhibits spherical symmetry. For instance, in the cartesian coordinate system, three coordinates (x, y, and z) are required to describe the surface of the sphere centered with the source. However, this surface can be described using radius (r) in a spherical coordinate system. This can lead to dramatic simplification in mathematics in some applications.

The root carriers in the spherical system are $\hat{r}$, $\hat{\theta }$, and $\hat{\varphi }$. As always, the dot output of the vectors on the same basis is equal to one and the dot output of the vectors on the opposite basis is equal to zero. For cross-products, we find

$\hat{r}\times \hat{\theta }=\hat{\varphi }$

$\hat{\theta }\times \hat{\varphi }=\hat{r}$

$\hat{\varphi }\times \hat{r}=\hat{\theta }$

The spherical system is not advised for determining absolute and relative positions. The reason is the same. In a spherical system, the base directions depend on the position. For instance, $r$ is defined radially externally at the source- $\hat{r}$=x for places along the x-axis but $\hat{r}$= y for places along the y-axis and $\hat{r}$= z for the positions along the z-axis. Similarly, the directions of $\hat{r}$ and are different as a function of position. To overcome this difficulty, it is common to introduce the problem into spherical coordinates and then switch to Cartesian coordinates at some point in the analysis.

Electromagnetic field theory

The electromagnetic field is a classical field generated by the acceleration of electric charges. This is the field described by classical electrodynamics and is equivalent to the quantized electromagnetic field tensor in quantum electrodynamics. The electromagnetic field can be identified as light as it propagates at the speed of light and it interacts with charges and currents. Its quantum counter is one of the four fundamental forces of nature.

The field can be seen as a combination of electric field and magnetic field. The magnetic field is generated by moving charges (currents) and The electric field is generated by constant charges; These two are often described as the source of the field. Maxwell equations and the Lorenz force law described the interaction of charges and currents with an electromagnetic field. The energy generated by the electric field is much more powerful than the energy generated by the magnetic field.

From a scientific point of view in electromagnetic history, the electromagnetic field can be thought of as a smooth, continuous field that propagates like a wave. In contrast, from the perspective of quantum field theory, this field appears to be quantitative; This means that the free quantum field (non-interacting field) is expressed as the Fourier of operator creation and destruction in the energy-momentum space as a whole, while the effects of the interacting quantum field can be evaluated and can be done in principle. Support for all mathematical techniques such as the Dyson series, Wicks theory, correlation functions, time-evolution operators, and Feynman diagrams.

Note that the quantitative field is still spatially constant; However, its energy states are discrete (the energy states of the field should not be confused with its energy values, they are continuous).

Vector analysis

A vector is a mathematical object that contains a scalar fraction (size and possibly a phase), as well as direction. Many quantities which are physical are best explained as vectors. For instance, the rate of motion through space can be explained as speed, i.e. standard international (SI) units are scalar with meter/seconds. However, this quantity is best described as a vector, i.e. its scalar part represents the speed and vector as the direction of motion. Similarly, force is a vector of which the scalar component represents the magnitude (SI base units of N) and the direction in which the force is applied. Electric and magnetic fields are also best explained as vectors.

Integration over length

In a spherical system, the differential-length section of the curve is represented as

$dl=r^{ }dr+{\theta }^{ }r d\theta +{\varphi }^{ }rsin\theta d\varphi$

Note that the distance is the opposite angle. $R\left(d\theta \right)$ in the direction of the corresponding distance. Also note that the distance $r\left(d\varphi \right)$ in the direction, z = 0 plane and z₀ factor is less than sinθ.

As always, the vector on the C curve is the sum of the A (r) field.

$\int A dl$

To demonstrate line integration in a spherical system, imagine a sphere with radius z = + a and z = −a with "poles" at the source. Let us calculate the integration of $A\left(r\right)=\hat{\theta }$, where C is the arc drawn from pole to pole directly along the surface of the sphere. In this example, dl =$\hat{\theta }$ a $d\theta$ because both r = a and (can be any value) are constant with C. Next, A⋅dl = a $d\theta$ and above is comprehensive

$\int a d\theta =\pi a$

As expected, half the circumference of the sphere.

Note that the spherical system is the correct choice for this example because the problem is expressed in the spherical system with a minimum number of different coordinates. If we try this problem in the Cartesian system, the finding of both z and x or y (or three) is relatively complex.

Context and Applications

This topic is important for professional exams in both graduate and postgraduate studies and in particular:

• Bachelors in Electrical Engineering
• Masters in Electrical Engineering

Practice Problems

Q1. Which of the following is the example of the spherical system?

1. Charge in space
2. Charge in box
3. Charge in dielectric
4. None of the above

Answer: Option a

Explanation: As the point charge in space spreads the electric field in all directions, the estimation of the electric field requires a spherical coordinate system.

Q2. In which of the following a test charge around any closed surface in a static path is zero?

1. Rotational field
2. Solenoidal field
3. Irrotational field
4. Conservative field

Answer: Option d

Explanation: In the conservative field, a test charge around any closed surface in a static path is zero.

Q3. Which of the following does not employ a waveguide?

1. Circular system
2. Spherical system
3. Both of the above
4. None of the above

Answer: Option b

Explanation: To avoid absorption there is no waveguide designed spherically.

Q4. Which of the following is the scalar factor of spherical coordinates?

1. 1, 1, 1
2. 1, r, r
3. r, r, 1
4. 1, r, rsin$\theta$

Answer: Option d

Explanation: In a spherical coordinate system radius varies from 1 to infinity and the plane angle from 0° to 360°, so the scalar form is 1, r, rsinθ.

Q5. Which of the following is also the spherical coordinate system?

1. Right-handed system
2. Left-handed system
3. Both a and b
4. None of the above

Answer: Option a

Explanation: Spherical system is also known as the right-handed system.