What is Buckling of column?
The column is described as a vertical member of the structure that carries an axial compressive load, and buckling is a lateral deformation of the column under the application of load.
Columns are classified into two types:
- Short column
- Long column
Short columns fail due to crushing or yielding of material under the compressive load, while long column fails by buckling due to compressive load.
When a long column is subjected to the compressive load, it deflects or bends in the lateral direction called buckling. Buckling does not vary linearly to the load acting on the column; it occurs suddenly.
The long column fails at excessive bucking, and the column's maximum load-carrying capacity is called critical load. The load-carrying capacity of a long column depends upon its length, moment of inertia of cross-section, type of support at ends, modulus of elasticity of column material, and many others.
The diagrammatical representation for the buckling of the column is shown as:
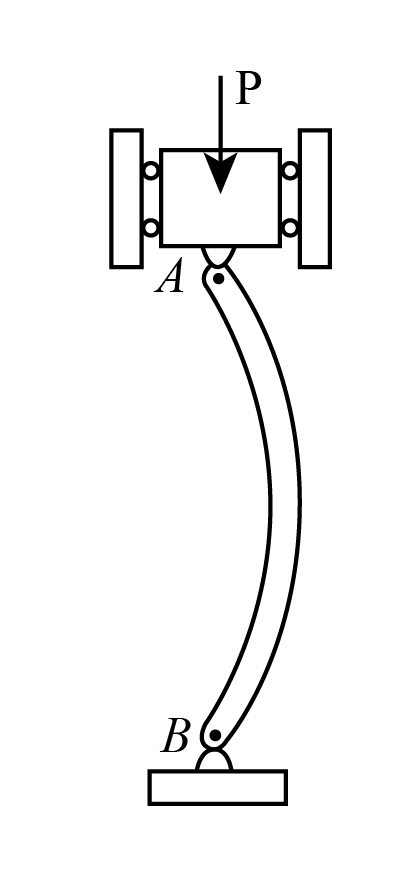
Euler's theory for buckling failure
Leonhard Euler derived a formula for the stability of a long column in 1757. Euler's theory states that the long column fails in buckling only. It neglects the effect of direct stress-induced in a long column as compared to the bending stress.
Derivation of the Euler's critical load for long column
Consider a long column AB of length l with both ends hinged, and P is the critical axial load of the column. The diagrammatical representation of the column is shown as:
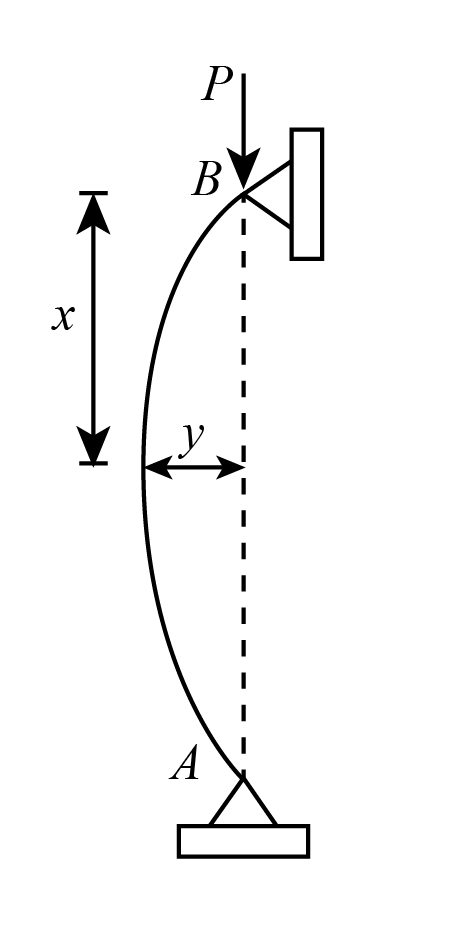
Take a sectional element at a distance x from upper-end B, and y is the lateral deflection at section.
The equation for the moment due to critical load about the section is as follows:
The above differential equation is solved as:
At
and
boundary conditions,
At
and
boundary conditions,
Now,
For failure in basic mode, the effective length of the column is taken. Therefore, the above equation is reduced as:
Here, n is the number of buckling loop.
Assumptions of Euler's theory
Following are the various assumptions of Euler's theory:
- The column is perfectly straight and of uniform cross section.
- The material of the column is homogenous and isotropic.
- The column is long and prismatic.
- The material of the column behaves elastically.
- The load acting on the column is perfectly axial and passes through its centroid.
- The column fails only in buckling.
- The self-weight of the column is neglected.
Effective length of Column
The effective length is described as a length within two sequential locations of zero bending moment over the beam.
Following are the basic cases of the effective length of a column based on its end condition:
- Both ends hinged
- Both ends fixed
- One end is fixed, and other end is free
- One end is fixed, and other end is hinged
Both Ends Hinged
In this case, both ends of the column are held in position but not restricted against rotation. The diagrammatical representation of column buckling is shown as:
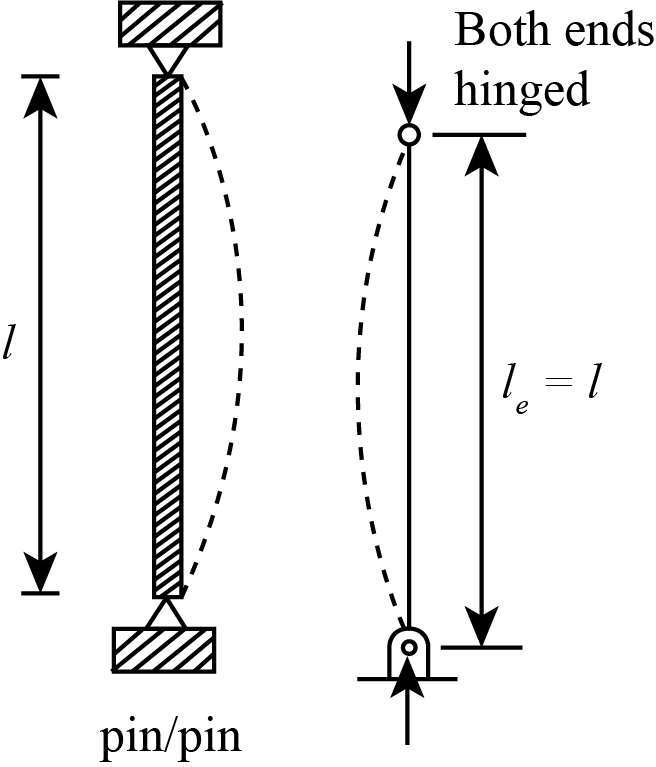
The effective length of the column having both ends hinged is
The critical load of the column having both ends hinged is as follows:
Both Ends Fixed
In this case, both ends of the column are held in position and restricted against rotation. The diagrammatical representation of column buckling is shown as:
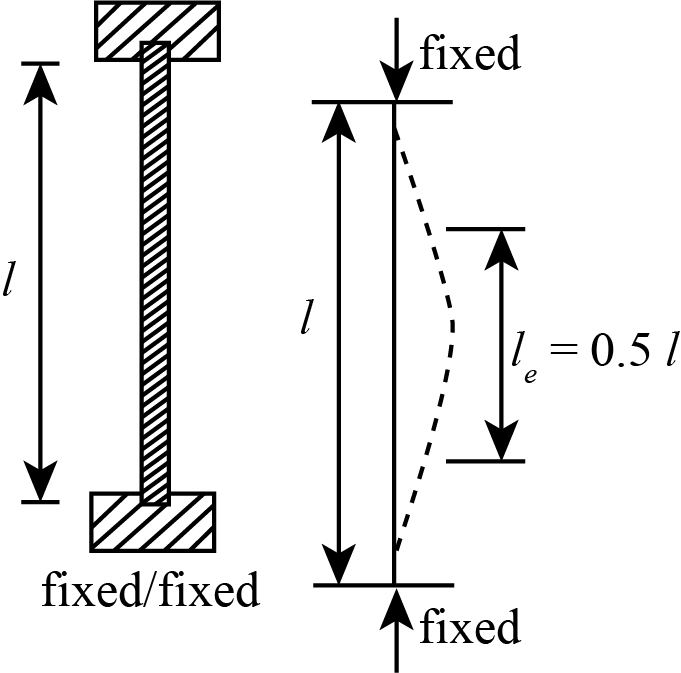
The effective length of the column having both ends fixed is
The critical load of the column having both ends fixed is as follows:
One end fixed and other end free
In this case, one end of the column is held in position and restricted against rotation, and the other end is free. The diagrammatical representation of column buckling is shown as:
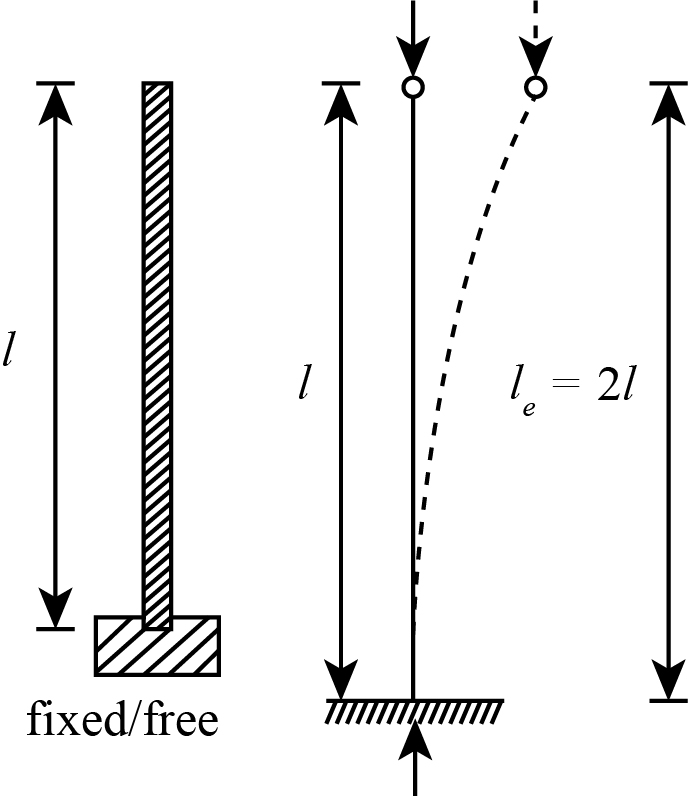
The effective length of the column having one end fixed and other hinged is
The critical load of the column having one end fixed and other free is as follows:
One end fixed and other hinged
In this case, one end of the column is held in position and resists against rotation, but the other end is held in position offers no restriction again rotation. The diagrammatical representation of column buckling is shown as:
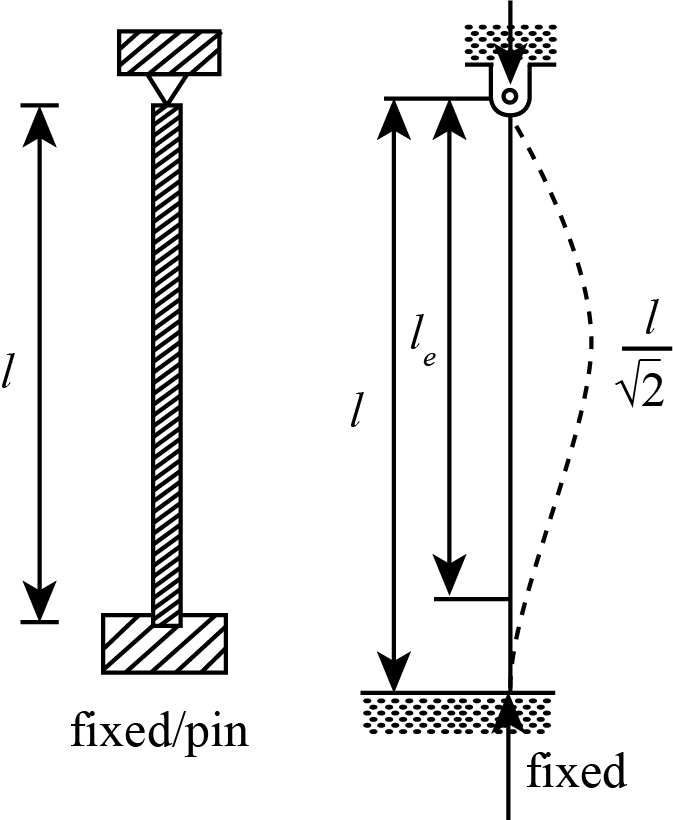
The effective length of the column having one end fixed and other hinged is
.
The critical load of the column having one end fixed and other hinged is as follows:
Slenderness ratio of column
The slenderness ratio of a column is the fractional relation between effective length and least radius of gyration. It is given as:
Radius of gyration
The radius of gyration is a term that gives the relation between moment of inertia and area of the system. It is given as:
Here, I is the moment of inertia, and A is the cross section area.
Limitations of Euler's theory
Following are the various limitations of Euler's theory:
- Euler's theory is valid only for long columns.
- It is valid only when the slenderness ratio is greater or equal to the critical slenderness ratio.
- Euler's formula is applicable when crushing stress is greater or equal to buckling stress.
What is Rankine's theory?
Rankine's theory
The small height columns fail due to crushing, and longer or larger height columns fail due to buckling. But practicality, the column fails due to the combined effect of crushing and buckling. Rankine's theory considered a combined form of failure, and Rankine's critical load is given as:
Here,
is crushing load,
is Euler's buckling load.
For
and
Here, is Rankine's constant, which depends on material properties like cross section, young's modulus, end condition, and others.
Common Mistakes
Following are the common mistakes performed by students:
- Sometimes, students forget that buckling does not vary linearly to the axial load acting on the column; it occurs suddenly.
- Sometimes, students forget the concept of the number of buckling loops.
- Sometimes, students get confused about the effective lengths of the column at different end conditions.
- Sometimes, students get confused between the assumptions and limitations of Euler's theory.
Context and Application
The topic buckling of columns is significant in various courses and professional exams of undergraduate, graduate, postgraduate, doctorate levels. For example:
- Diploma in Mechanical Engineering
- Diploma in Civil Engineering
- Bachelor of Technology in Mechanical Engineering
- Bachelor of Technology in Civil Engineering
- Master of Technology in Structural Engineering
- Doctorate of Philosophy in Structural Design
Related Concept
- Beams and Columns
- Truss and Structural Analysis
- Young's Modulus
- Stress due to axial load
Practice Problems
Q1. Buckling is mainly occurred in which of the following?
- Short beam
- Short column
- Long column
- None of these
Correct option: (c)
Q2. Which of the following is correct Euler's formula?
- None of these
Correct option: (a)
Q3. In which case, the effective length of the column is twice the column length?
- Both end hinged
- One end fixed and other end free
- Both end fixed
- One end fixed and other end hinged
Correct option: (b)
Q4. The formula for the slenderness ratio is _____?
Correct option: (d)
Q5. Which of the following failure is considered in Rankine's theory?
- Crushing failure
- Buckling failure
- Crushing and buckling failure
- None of these
Correct option: (c)
Want more help with your mechanical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Buckling of columns Homework Questions from Fellow Students
Browse our recently answered Buckling of columns homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.