What is the meaning of center of gravity?
The term center of gravity indicates the position or location of a point about which the whole weight of a body or system is supposed to be concentrated, which means the whole weight of the body or system works through this point. It is closely related to mass distribution. For all positions of the body, the center of gravity would be a single point.
What is the meaning of centroid?
The term centroid indicates the position or location of a point about which the whole area or volume of a body or system can be concentrated. In other words, it represents the geometric center of the area or volume, and sometimes it can be outside of the body or area. It is closely related to length, area, or volume distribution and is generally useful in two-dimensional problems. The concept of the first moment of the area helps to obtain the centroid of an area.
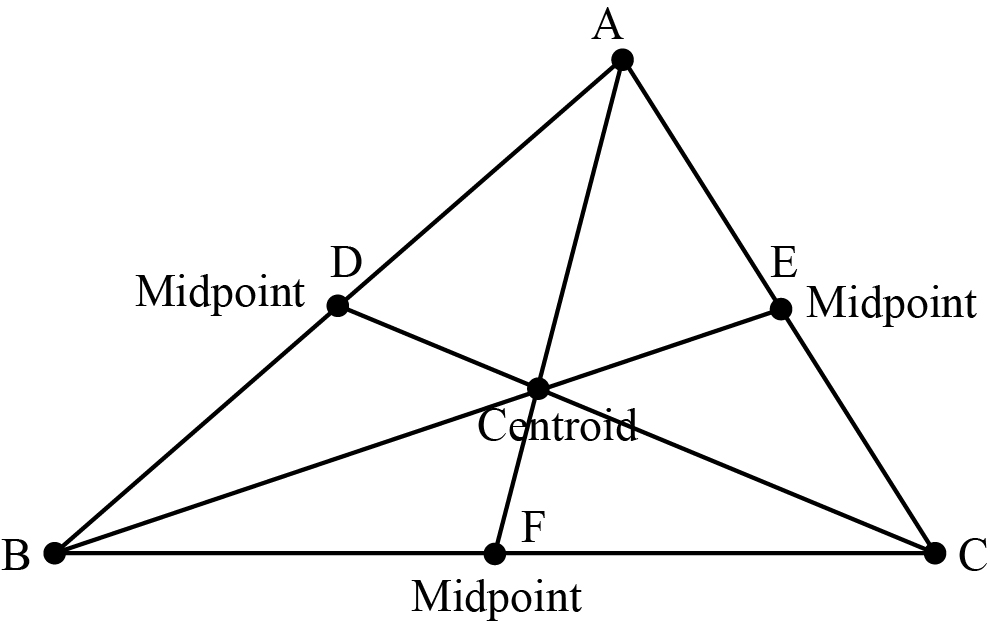
Difference between center of gravity and centroid
A body or structure is made up of an infinite number of small particles of differential size, and every particle has some differential weight. The total weight of the body would be the sum of the individual weight of all particles, and the total weight would pass through a specific point, which refers to the center of gravity. The basic difference between the center of gravity and centroid of a body or structure is given below in the following points.
- Center of gravity applies to the object or body with a particular mass and weight, whereas the term centroid is applicable to plane areas.
- Center of gravity represents a point in a body or object through which the total gravitational force means the weight of the body acts for any orientation of the body or object, whereas in a plane area, centroid represents a point such that the moment of the area through the point about any axis would be equal to zero.

Center of Gravity
- Whenever a body of specific weight consists of infinite number of particles of differential weight placed in a co-ordinate system, then the moment of the resultant force about any axis is equal to the sum of the moments of the weight of the individual particles about the same axis.
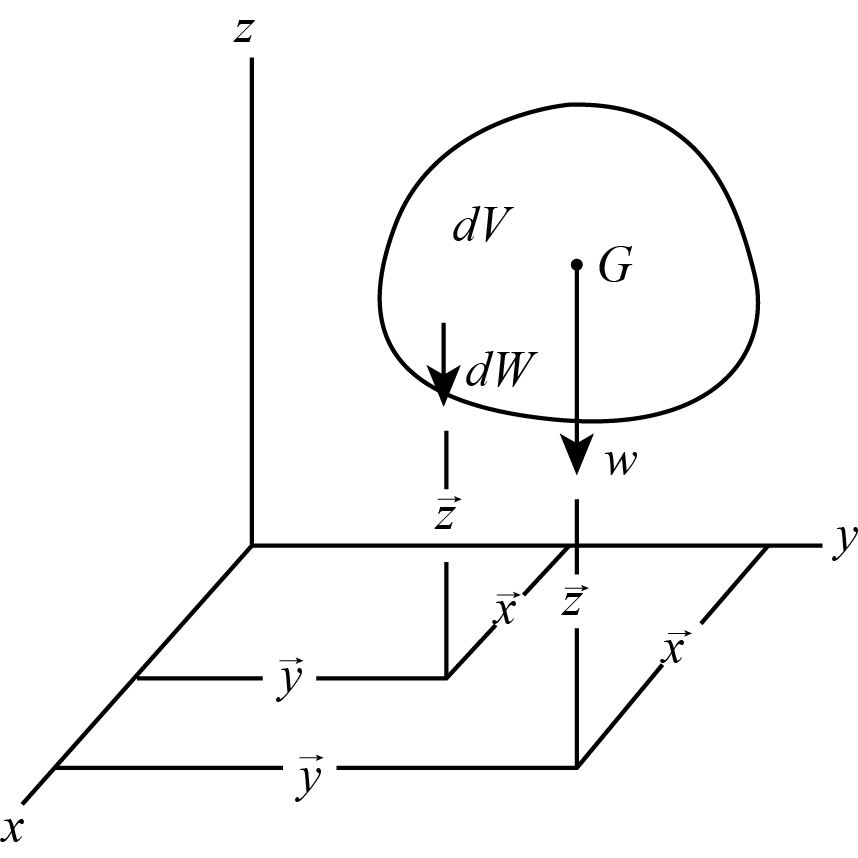
The mathematical expression for the center of gravity of the body with respect to the and z axis can be represented as,
Centroid
Whenever an object has an axis of symmetry, then the centroid of the object would be lying on the object's axis, whereas in some of the cases centroid would not lie on the object; it may be outside the object. The position of the center of gravity will be the same as the position of the center of mass of an object if the material of the object is homogeneous throughout the body.
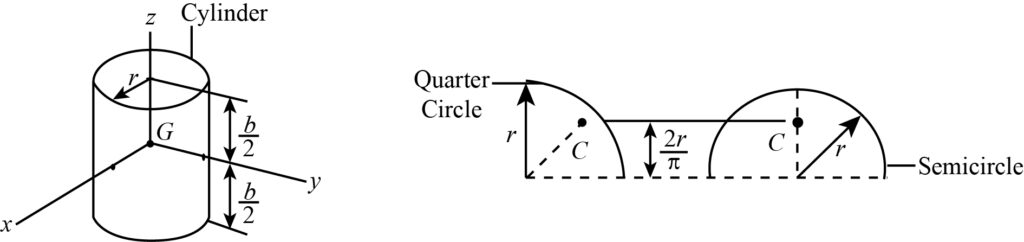
Centroid of a regular shape body
- The centroid of a regular shape area or line would lie somewhere on the line of symmetry.
- If the line of symmetry is two or more, then centroid would lie on their intersections.
- For a volume, the centroid would lie on a plane of symmetry.
- If there are two or more planes of symmetries in a volume, the centroid will lie on a line created by their intersections.
Methods to determine the centroid of an object
Three methods help to obtain the centroid of an object: integration method, composites method, and solid modeling software.
Integration method
Whenever the expression of area, volume, or line of a body is given, then the value of the centroid of the body can be obtained with the help of integration method by using the following steps:
- First select an appropriate differential rectangular element of differential area in a body of total area at a general point in the body. If can easily be expressed in terms of , then select the vertical rectangular element in the whole area of the body and if can easily be expressed in terms of , then select the horizontal rectangular element in the whole area of the body.
- Now represents the differential area in terms of and .
- Evaluate co-ordinates of the rectangular element in terms of general point .
- In the formula of integration method, put all the integral limits and variables and then integrate the integration using definite integral rules.
The mathematical expression of integration method to obtain centroid of a body can be represented as,
Here, and represent the co-ordinates of the centroid of the body.
Composites method
Many industrial objects are made up of a number of different simple shapes of objects. The entire object is considered a composite object. Whenever a body can divide into a relatively simple shape of known centroids, the value of the centroid of the total body can be obtained with the help of the weighted average of the centroid of the composites by using the following steps:
- First, divide the entire area into the number of simple standard shapes of the known centroid.
- Find the centroid of each smaller standard shape that is known to us in the form of standard value.
- Now, calculate the weighted average of the centroid of the whole area of the body with the help of this method.
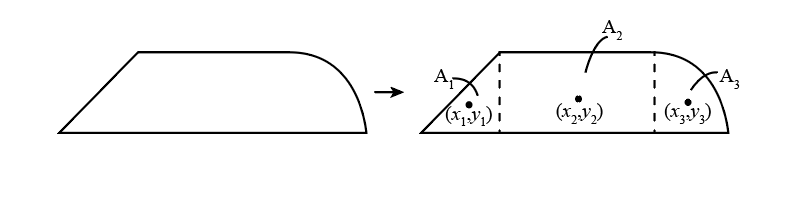
The mathematical expression to calculate the centroid of a two-dimensional object can be represented as,
Here, and represents the co-ordinates of the centroid of the object.
Solid modeling software
To construct a 3D model of an object, auto-cad, solid-works, etc., helps, and these software also help to obtain the centroid of the object as well as volume, moment of inertia, etc.
Centroid of a line
Whenever a specific curve line bar of specific weight is placed in three-dimensional co-ordinate axes, the value of the coordinates of the centroid of the curve line bar can be obtained by using the given integral expression:
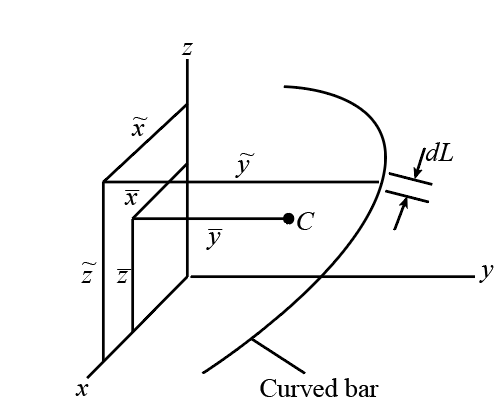
Here, , and represent the co-ordinates of the centroid of the curve line bar.
Centroid of an area
Whenever a curve plate of specific area and thickness is uniform throughout the area then, the value of the coordinates of the centroid of the curve area can be obtained by using the given expression.

Here, , and represents the co-ordinates of the centroid of the curve plate area.
Center of gravity of three-dimensional body
Whenever a three-dimensional body has a specific weight and volume, then the coordinates of the centroid of the body can obtain with the help of a given mathematical expression.
Here, , and represents the co-ordinates of the centroid of three-dimensional body, represents the differential length along the curve bar, and represents the total length of the curve bar.
Application of center of gravity and centroid
The concept of the center of gravity is very important in the field of design. Some important applications of center of gravity are given below in the following points.
- In the design of concrete structure.
- In the design of metal structure.
- In the design of railway bridges.
- In the design of highways.
- In the design of water dams.
- In the design of water tanks.
- In the design of automobiles.
Common Mistakes
- Students sometimes get confused about the difference between the center of gravity and centroid. However, the center of gravity represents a point through which the total weight of the body acts, whereas the centroid represents the geometric center of the body.
- Sometimes, students also get confused about the difference between the center of gravity and the center of mass. However, the center of mass defines the mass distribution in space, and if the material of an object is homogeneous throughout, then the center of mass and the center of gravity would be the same.
- The student also gets confused about whether the center of gravity and centroid can lie outside the geometric boundaries of the body. However, there is a possibility that the center of gravity and centroid can lie outside the geometric boundaries of the body.
Contexts and Applications
Center of gravity and centroid is very significant in the several professional exams and courses for undergraduate, Diploma level, graduate, postgraduate. For example:
- Bachelor of Technology in Mechanical Engineering
- Bachelor of Technology in Civil Engineering
- Master of Technology in Mechanical and Civil Engineering
- Doctor of Philosophy in Mechanical Engineering
Related Concepts
- Center of mass
- Uniform density of body
- Non-uniform density of body
- Gravitational force
- Geometric center
- First moment of area
- Composites plates and area
- Quarter circular shape
- Semicircular shape
- Axis of symmetry
- Center of area
Practice Problems
Q1. Which of the following option is correct regarding the point through which the total weight of a body acts?
a. Center of gravity
b. Centroid
c. Central point
d. Inertial point
Correct option: (a)
Explanation: The Center of gravity is the point at which the total weight of any object is concentrated. It is considered a hypothetical point at which the gravity force will act. With the help of a simple physical process, the centroid can be easily determined.
Q2. The point through which the total area of a plane body is considered to be concentrated is known as
a. Central point
b. Centroid
c. Center of gravity
d. None of these
Correct option: (b)
Explanation: Arithmetic means the position of all the given points in the diagram can be determined with the help of the centroid. The Center of gravity is different from the centroid. The Center of gravity tells about the point at which the total weight of any specific body is situated.
Q3. The center of gravity of a uniform rod/bar lies at,
a. At the center of the cross-section
b. Depends upon its material
c. At the middle of the rod
d. None of these
Correct option: (c)
Explanation: The center of gravity of a rod will act on the point where the total weight of the uniform rod will be concentrated. The rod is considered as the linear object having constant linear density. It will be located in the middle of the rod.
Q 4. When an object has no uniform density throughout its whole area, then which of the following option is correct regarding the location of centroid and center of mass?
a. Independent upon the density
b. Lie at same point
c. Does not lie at the same point
d. None of these
Correct option: (c)
Explanation: When the object is non-uniform and has no uniformity in the body's density, then the centroid and center of mass will not lie at the same point. The center of gravity of a uniform body is considered the same as the center of mass.
Q5. Which of the following options is correct regarding the position of the centroid of an object with an axis of symmetry?
a. On the axis of symmetry
b. Out of the axis of symmetry
c. Outside the object
d. None of these
Correct option: (a)
Explanation: If any object has an axis of symmetry, then the centroid will lie on that axis of symmetry. If the same body has two or more two axes of symmetry, then the centroid will coincide at the intersection of those axes.
Want more help with your mechanical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Mechanics
Fundamental Concepts of Mechanics
Center of Gravity and Centroid
Center of Gravity and Centroid Homework Questions from Fellow Students
Browse our recently answered Center of Gravity and Centroid homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.