What is the meaning of vibration?
Whenever an object/system displaces in either side of its equilibrium position with the help of an external/internal means, then the object/system moves regularly or randomly on both sides of its equilibrium position. This motion is called vibration. Generally, there are three types of vibration: longitudinal vibration, transverse vibration, and torsional vibration.
What is free vibration?
Free vibration is a type of vibration in which the external force is removed after giving the initial displacement to a body/system, after which the system continues to vibrate at its natural frequency.
What do you mean by undamped vibration?
Undamped vibration is a type of vibration in which no resistance force/friction force acts on the vibrating system. In such cases, the system oscillates with no loss of energy, which means the system continues to vibrate at its natural frequency.
What are free undamped vibrations?
- Free undamped vibration is a type of vibration in which a system encounters no outside resistive force (damping) to the vibration, and the externally applied force is removed after giving the initial displacement to the system.
- Whenever the value of the frequency of the external force is the same as the natural frequency of the vibrating system, then there would be a condition of resonance. In such cases, the value of the amplitude of vibration would be very large, which could result in the possibility of failure of the system/body. The value of the natural frequency of a system/body depends on parameters like geometry, system mass, etc.
Methods to obtain natural frequency of free undamped vibrations
Generally, there are three methods to obtain the equation and the natural frequency of the vibrating system: the equilibrium method, the energy method, and Rayleigh's method. The basic details about these are given below.
Natural frequency of free undamped vibration by equilibrium method
Whenever a system/body is not in a static equilibrium due to acceleration of motion, then the system/body can be brought to its static equilibrium state with the help of an inertia force acting on it. The value of inertia force is obtained by taking the body's mass and the direction opposite to body acceleration.
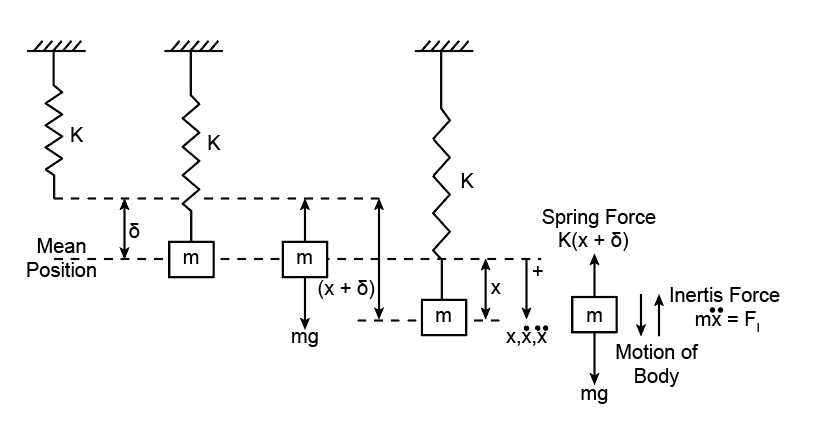
The forces acting on the mass are inertia force, spring force, and gravitational force. According to the equilibrium method, by using the D'Alembert principle, the expression of the angular frequency of free undamped vibration can be represented as,
Here, represents the angular frequency of vibration, represents the spring constant, and represents the mass of attached object with spring.
The fundamental expression of simple harmonic vibrating one degree of motion can be represented as,
The fundamental expression of natural frequency of vibration can be represented as,
Here, represents the natural frequency of vibration.
Natural frequency of free undamped vibration by energy method
- According to the energy conservation principle, no energy can transfer to the vibrating system or transfer out from the vibrating system in free undamped vibration. So, the total energy, or the sum of kinetic energy and potential energy, would remain constant. The term kinetic energy exists due to the system's motion, whereas potential energy consists of two parts: gravitational potential energy and strain energy.
- Gravitational potential energy is due to the position of the vibrating body with respect to the equilibrium position, whereas strain energy exists due to the elastic deformation of the system. At the equilibrium position, kinetic energy would be maximum, whereas potential energy would be zero; at the extreme position, kinetic energy becomes zero, and potential energy becomes maximum.
According to this method, the fundamental expression of simple harmonic motion can be represented as,
The expression of angular frequency of free undamped vibration can be represented as,
The fundamental expression of natural frequency of vibration can be represented as,
Here, represents the natural frequency of vibration, represents the angular frequency of vibration, represents the spring constant, and represents the mass of attached object with spring.
Natural frequency of free undamped vibration by Rayleigh's method
- Rayleigh's method is an extension of the energy method. According to the energy conservation principle, total energy at the mean position of a vibrating system is equal to the total energy at the extreme position of the motion. As we know, at the mean position, kinetic energy would be maximum, whereas, at the extreme position, potential energy would be maximum.
- According to this principle, the maximum energy at the mean position would equal the maximum potential energy.
The fundamental expression of the natural frequency of vibration can be represented as,
Free undamped transverse vibration
- It is a type of vibration in which the deflection takes place in the perpendicular direction of the longitudinal axis, that is, in the transverse direction. Let us consider a cantilever beam connected with a mass at its free end. There would be deflection in the transverse direction due to the gravitational force of mass.
- The system is subjected to one-time external force, and it will displace from its equilibrium position. Forces acting on the mass beyond the mean position are inertia force and resisting upward force.
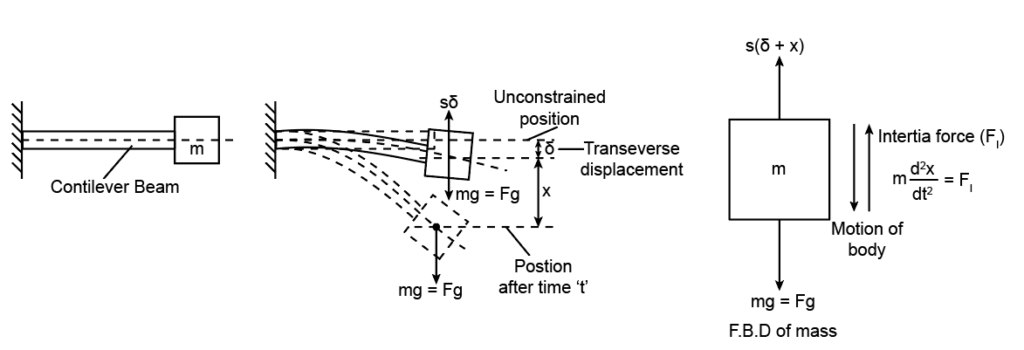
The expression of angular frequency of free undamped transverse vibration can be represented as,
Here, represents the angular frequency of transverse vibration, represents the transverse displacement, and represents the gravitational acceleration.
The expression of natural frequency can be represented as,
Here, represents the natural frequency of transverse vibration.
Free undamped torsional vibration
- Torsional vibration occurs whenever a rigid body/system oscillates about a specific reference axis. In this vibration, the displacement of the body is in the form of angular displacement.
- Let us consider a disc of specific mass moment of inertia suspended on a circular shaft of negligible mass. Suppose the disc is given angular displacement in the clockwise direction about the shaft axis. In this case, it starts vibrating about the axis of the shaft, and such vibration is called torsional vibration.
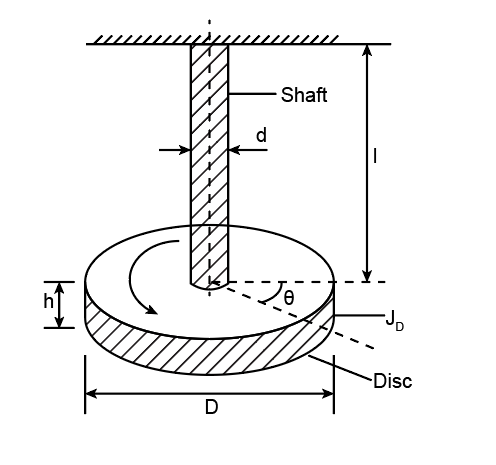
According to D'Alembert's principle, the fundamental expression of simple harmonic free undamped vibration can be represented as,
Here, represents the angular frequency of vibration.
The expression of fundamental frequency of vibration can be represented as,
Here, represents the natural frequency of vibration, represents the torsional stiffness of shaft, and represents the mass moment of inertia of disc.
Common Mistakes
- Students sometimes get confused about the difference between damped vibration and undamped vibration. In undamped vibration, there is no resistive force (friction/drag etc.) acting on the vibration, whereas in damped vibration, an external resistive force acts so that loss of energy occurs.
- Students may also get confused regarding free vibration and natural vibration. Free vibration and natural vibration are both similar.
- Another point of confusion is related to the units of fundamental quantities. Always use standard international units to calculate frequency, angular frequency, vibration's amplitude, and other physical quantities. For example, the amplitude will be measured in standard units meter.
Context and Applications
The topic of free undamped vibration is significant in the several professional exams and courses for the undergraduate, Diploma, graduate, and postgraduate levels. For example:
- Bachelor of Science in Physics
- Bachelor of Technology in Mechanical Engineering
- Bachelor of Technology in Civil Engineering
- Masters in Technology in Mechanical Engineering
- Doctor of Philosophy in Mechanical Engineering
Related Concepts
- Forced vibration
- Damped vibration
- Underdamped vibration
- Oscillation
- Simple pendulum
- Inertia force
- D'Alembert's principle
Practice Problems
Q 1. Which of the following options is correct about salient features of any vibration?
- Amplitude and frequency
- Amplitude and acceleration
- Frequency and acceleration
- None of these
Correct answer: (a)
Explanation: In the above options, amplitude and frequency describe the phenomenon of vibration. Amplitude gives the maximum distance on either of any sides in any fixed position. And frequency gives the number of any events in a unit time interval.
Q 2. What is the speed of motion of a vibrating object during a vibration?
- Constant
- Variable
- Can't say
- None of these
Correct answer: (b)
Explanation: It can vary from zero to maximum values. It cannot be a constant value. Speed can vary during each cycle in a vibrating object's motion. A vibrating type of object can repeat its specific motion at a particular time.
Q 3. Which of the following options is correct regarding mechanical vibration?
- Undesirable
- Desirable
- None of these
- Both (a) and (b)
Correct answer: (d)
Explanation: Mechanical vibration can be desirable and undesirable (both) forms of energy. A simple motion can produce it or be produced by mechanical force. For example, the tuning force can be considered a desirable vibration form.
Q 4. The phenomenon of free vibration of a system comes from
- Initial disturbance
- Continuous disturbance
- Both (a) and (b)
- None of the above
Correct answer: (a)
Explanation: The vibration occurs from the initial disturbance. When anyone provides some input, then the body can vibrate freely. The free vibration can be of two types: damped and undamped.
Q 5. Which of the following options is correct regarding the existence of mechanical vibration?
- In elastic bodies
- In inelastic bodies
- Both (a) and (b)
- None of the above
Correct answer: (a)
Explanation: The existence of mechanical vibration can be observed in elastic bodies. Anybody who possesses oscillatory motion. It will consist of the elastic forces and the inertia due to which it will oscillate. They can be described by elastic vibration.
Want more help with your mechanical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Free undamped vibrations Homework Questions from Fellow Students
Browse our recently answered Free undamped vibrations homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.