What is Moment of Inertia?
When a rigid body is in rotational motion, it requires a torque for a desired angular acceleration about its axis. Moment of inertia is the determination of this torque which is proportional to the mass of the body and square of the distance from the rotation axis. The mass of the rigid body also determines the force needed for the desired acceleration. The axis chosen is also responsible to determine the torque required to change the rotation of the body.
Inertia
Inertia can be termed as a resistance offered by a body to change its state. A rigid body initially at rest will apply resistance when acted by an external force that tends to change its state of rest or velocity, or a body initially at motion will provide resistance in changing its state of velocity or motion for coming to a state of rest. In other words, Newton's first law of motion describes the law of inertia of a rigid body.
Inertia is proportional to the mass of a body, more the mass of a body, more the resistance it will apply in changing its state.
Inertia is a property possessed by a rigid body while it is undergoing linear motion (one-dimensional motion), curvilinear motion (two or three-dimensional motion) and rotational motion. The inertia possessed by a body while undergoing rotational motion is termed rotational inertia.
Beams and Moment of inertia
Beams are the members that are always under the action of lateral loads or shear loads. Under such loading conditions, they undergo deformations such as bending and deflections. In such conditions, the top fibers of the beam are under tension and the bottom fibers are under compression. There exists a bending stress distribution along the cross-section of the beam that varies linearly. The stress magnitudes are maximum at the top fibers and bottom fibers. However, there exists a central section along the cross-section of the beam known as the neutral axis, where the centroid of the cross-section lies. The bending stress distribution along the neutral axis is zero.
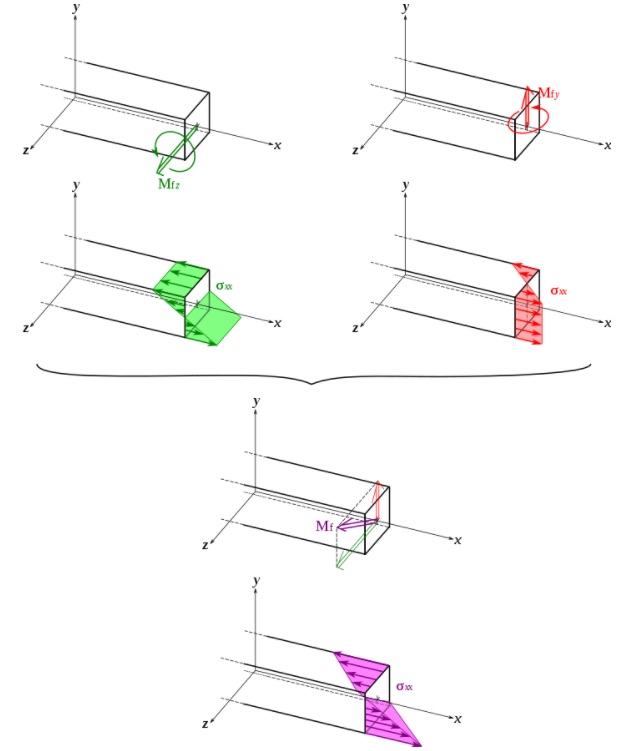
The stress distribution can be replaced by a system of parallel forces. As can be seen from the above figure, the system of parallel forces are equal and opposite, above and bottom of the cross-section of the beam. This force distribution tends to rotate the beam about the neutral axis of the beam. The beam, due to its cross-section and material properties, tries to apply resistance to this bending.
Hence, the moment of inertia is a measure of resistance to bending under the influence of external loading.
The second moment of an area or moment of inertia
Area moment of inertia or second area moment or quadratic area moment or moment of inertia is a property of a two-dimensional geometrical section that reflects how its points are distributed along with the plane space of the two-dimensional section about a fixed axis.
The second moment of area is represented by the letter (for area moment of inertia along the axes which are parallel to the cross-section) or (for area moment of inertia along an axis that is perpendicular to the cross-section). The area moment of inertia denoted by the letter is also known as the polar moment of inertia.
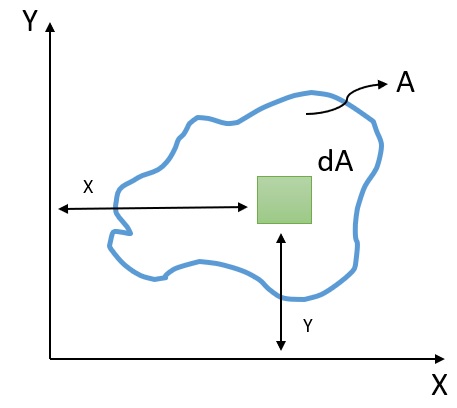
Consider a plane arbitrary cross-section of area . Consider an infinitesimal cross-sectional area inside the arbitrary cross-section.
The first moment of the small elemental area with respect to the axes and can be written as,
and,
Consider the moments of the first moment of the elemental area, ; and accordingly, the above equation can be written as,
and,
Hence, to calculate for the entire area, , the above expression should be integrated with respect to the entire area
Hence, the above expressions are written as,
…(a)
and, …(b)
Equations (a) and (b) are known as the second moment of area or moment of inertia about and -axis, respectively. In the equations, the and axis is known as the rotational axis.
Radius of gyration
The radius of gyration is a function of the second moment of area, and it is a fundamental property considered during the designing of columns. The property indicates the stiffness or the strength it provides to bending when the member is used as a vertical member under the action of compressive loads.
The radius of gyration is defined as the distance from the axis to a point, where the entire area can be concentrated along a strip, having the same moment of inertia with respect to the given axis.
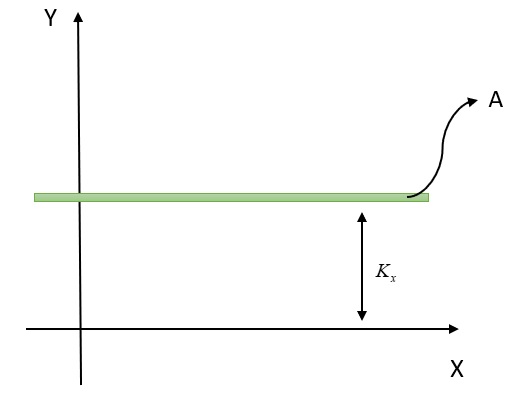
Concentrating the entire area of the arbitrary cross-section into a thin strip of the same area as shown in the above figure, the moment of inertia with respect to the -axis can be written as,
The term, is termed as the radius of gyration.
During calculation, the value of the radius of gyration can be calculated by the following equation,
Similarly, can be calculated, knowing the value of .
Transfer formula or parallel axis theorem
In practical situations, while designing members, a situation arises for the determination of the moment of inertia about different axes. Knowing the moment of inertia about the centroidal axis, the moment of inertia about the other axis or a non-centroidal axis can be estimated. The non-centroidal axis should be parallel to the centroidal axis. Using a theorem, called the parallel axis theorem of transfer formula, the moment of inertia about a non-centroidal axis can be calculated, having known the moment of inertia about the centroidal axis.
The formula relates the moment of inertia of any area with respect to any axis, provided the axis is parallel to the centroidal axis of the plane laminae.
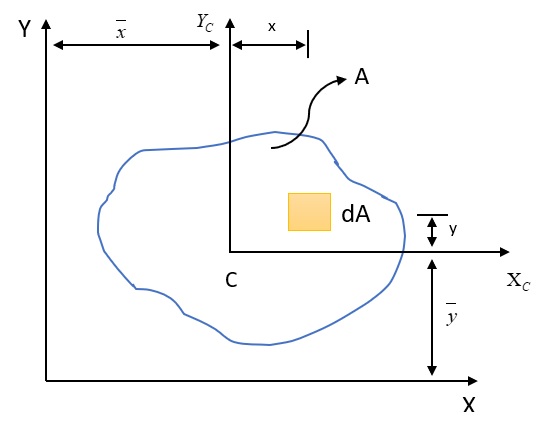
Consider an arbitrary plane of cross-section area . and are the centroidal axes passing through the centroid, of the cross-section. and are the two principal axes (non-centroidal axes) or the global coordinate axes.
Consider a small elemental area, inside the arbitrary cross-sectional area , the moment of inertia of the elemental area with respect to reference axes and is given as
…(a)
and, …(b)
Where,
= Moment of inertia about the axis
= Moment of inertia about the axis
= Moment of inertia about the centroidal axis
= Moment of inertia about the centroidal axis
Perpendicular axis theorem or polar moment of inertia
Just as the moment of inertia about the centroidal axes gives a measure of resistance to bending, the polar moment of inertia gives a measure of resistance to torque or twisting along the perpendicular z-axis of the plane cross-section.
When any external torsional twist or torque is applied, the body tries to resist that torque by inducing a resistance, that resistance is known as polar moment of inertia.
An expression for the polar moment of inertia is derived using the perpendicular axis theorem.
The equation for polar moment of inertia with respect to the perpendicular z-axis is given as
Where,
= Distance of an elementary small area from the z-axis given radius
= Polar moment of inertia about the z-axis or the perpendicular axis
Moment of inertia of some elementary shapes
- Moment of inertia of a rectangle having its length L
The moment of inertia of a rectangular plane profile having its length L and height, h, with respect to the centroidal axis x, is given by,
- Moment of inertia of a triangle having its base b and height h
The moment of inertia with respect to the centroidal axis x, of a triangular cross-section of base b and height h is given by,
- Moment of inertia of a circle of radius r
The moment of inertia with respect to the centroidal axis x, of a circle of radius r is given by,
Context and Applications
The topic of is extensively taught in courses such as,
- Bachelor of Technology (Engineering applications)
- Bachelor of Technology (Structural engineering)
- Bachelor of Technology (Mechanical engineering)
- Masters in Science (Physics)
- Masters in Science (Applied Mechanics)
- Bachelors in Science (Physics)
- Bachelors in Science (Applied Mechanics)
Practice Problems
- Which of the following is the other name of the transfer theorem?
- Parallel axis theorem
- Perpendicular axis theorem
- Both are used in the same context based on the position of the centroidal axes
- None of these
Correct option- a
Explanation: The transfer axis theorem is also known as the parallel axis theorem. It is used to determine the moment of inertia of the non-centroidal axes provided, the axes are parallel to the centroidal axes.
2. Which of the following requires the application of the perpendicular axis theorem?
- Moment of inertia about the principal axes
- Moment of inertia about the centroidal axes
- Polar moment of inertia
- None of these
Correct option- c
Explanation: The moment of inertia about the z-axis is known as the polar moment of inertia and the method to determine an expression for it is given by the perpendicular axis theorem.
3. Which of the following expressions represents the polar moment of inertia ?
Correct option- b
Explanation: Using the perpendicular axis theorem, the polar moment of inertia of a small elemental area , the expression for moment of inertia about the z-axis is given by
4. Which of the following expressions represents the area moment of inertia of a triangle of base b and height 'h'?
Correct option- a
Explanation: The area moment of inertia of a triangle of base b and height h is given by
5. Which of the following is the other term for the second moment of the area?
- Area moment of inertia
- Centroid
- Mass moment of inertia
- None of these
Correct option- a
Explanation: The second moment of area is also known as the area moment of inertia.
Related Concepts
- Mass moment of inertia of a thin rod
- Mass moment of inertia of a rotating disc
- Area moment of inertia of a thin circular strip
- Inertia tensor
- Representation of slug-ft2 in dimensional quantity
Want more help with your mechanical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Moment of Inertia Homework Questions from Fellow Students
Browse our recently answered Moment of Inertia homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.