What is the slope and deflection of a beam?
The slope in a deflected beam is described as an angle in radians made by the tangent of the section with the original axis of the beam. The deflection at any point on the axis of the beam is defined as the lateral displacement of the point before and after loading.
Why do we study the slope and deflection of a beam?
We see that whenever a cantilever or a beam is loaded, it deflects from its original position. The amount of deflection in the beam is a function of its cross-sectional area and bending moment. Following are the two design criteria for the deflection of a cantilever or a beam:
- Strength
- Stiffness
Based on the strength criterion of the beam design, it should be strong enough to resist the bending and shear force. In other words, the beam should be strong enough to resist the bending stresses and shear stresses induced during loading.
And based on the stiffness criterion of the beam design, which is equally important, it should be stiff enough to resist the deflection of the beam. In other words, the beam should be stiff enough not to deflect more than the permissible limit under the loading action.
Some specifications are always laid to limit a cantilever's maximum deflection or a beam to a small fraction of its span in the practical world.
Methods for determining slope and deflection at a section by double integration method
We already know that,
where is the bending moment of the beam, is the flexural rigidity of the beam, is the Young's modulus, I is the moment of inertia.
Integrating the above equation,
Here, is the slope of the beam. Now integrating the above equation once again,
Here, is the deflection of the beam at any point, and represents the constant of integration.
Macaulay's method for slope and deflection
The problem of deflections in the beam is tedious and laborious when the beam carries some point loads. Mr W.H. Macaulay introduces a method, a continuous expression, for bending moment and integrating it so that the constants of integration are valid for all beam sections, even though the law of bending moment varies from to section.
NOTE: Following are the various rules for applying Macaulay's method:
- Always take the origin or reference point on the extreme left of the beam.
- Take a left clockwise moment as negative and left anticlockwise moment as positive.
- While calculating the slopes and deflections, it is convenient to use the values first in terms of and meters.
Moment area method
The term moment area method refers to a graphical process to determine the slope and deflection of beams. It is based on Mohr's theorems which are stated below:
Mohr's Theorems
Mohr's Theorem-I: It states, "The slope difference between any two points, on an elastic curve is equal to the net area of bending moment diagram among these points divided by the flexural rigidity ."
In equation form, it can be written as,
Mohr's Theorem-II: It states, "The intercept taken over a vertical reference line of tangents intersecting at any points on an elastic curve, is equal to the moment of the bending moment diagram among these points about the reference line divided by EI."
In equation form, it can be written as,
Conjugate beam method
The conjugate beam method is described as a revised form of the moment area method. It is conveniently used to determine the slope and deflection of cantilevers and supported beams. This method is specially used for beams and cantilevers with varying flexural rigidities.
Conjugate beam: Conjugate beam is described as an imaginary beam of length equal to that of the original beam, width equal to 1/EI, and loaded with the usual bending moment diagram. The slope and deflection is then found out by following two theorems known as Mohr's theorems.
Mohr's First Theorem: According to this theorem, the value of shear force at a specific section of a conjugate beam would be equal to the slope of the elastic curve.
In equation form, it can be written as,
Mohr's Second Theorem: According to this theorem, the value of bending moment at a specific section of a conjugate beam would be equal to the deflection of the elastic curve.
In equation form, it can be written as,
| S. No. | Actual Beam | Conjugate Beam | Remarks |
| 1. | Fixed end | Free end | Slope and deflection at the fixed end of the actual beam are zero. Shear force and bending moment at the free end of the conjugate beam are also zero. |
| 2. | Free end | Fixed end | Slope and deflection at the free end of the actual beam exist. Shear force and bending moment at the fixed end of the conjugate beam also exist. |
| 3. | Simply supported or roller supported end | Simply supported end | Slope at free end of the actual beam exists. But deflection is zero. Shear force at the simply supported end of the conjugate beam exists. But the bending moment is zero. |
Strain energy or Castigliano method
Carlo Alberto Castigliano gives Castigliano's method for obtaining the displacement magnitudes of a linear-elastic system that works on the partial derivatives of energy.
Castigliano's first theorem (For determining forces in an elastic structure): If the strain energy of an elastic structure can be expressed as a function of generalized displacement , then the partial derivative of the strain energy with respect to generalized displacement gives the generalized force .
In equation form,
where U is the strain energy.
If the force-displacement curve is non-linear then the complementary strain energy needs to be used instead of strain energy.
Castigliano's second theorem (For determining displacements in a linearly elastic structure): If the strain energy of a linearly elastic structure can be expressed as a function of generalized force , then the partial derivative of the strain energy with respect to generalized force gives the generalized displacement in the direction of .
As above this can also be expressed in the equation as:
Slope and Deflection of beams under different loading/support conditions
For Cantilever beam
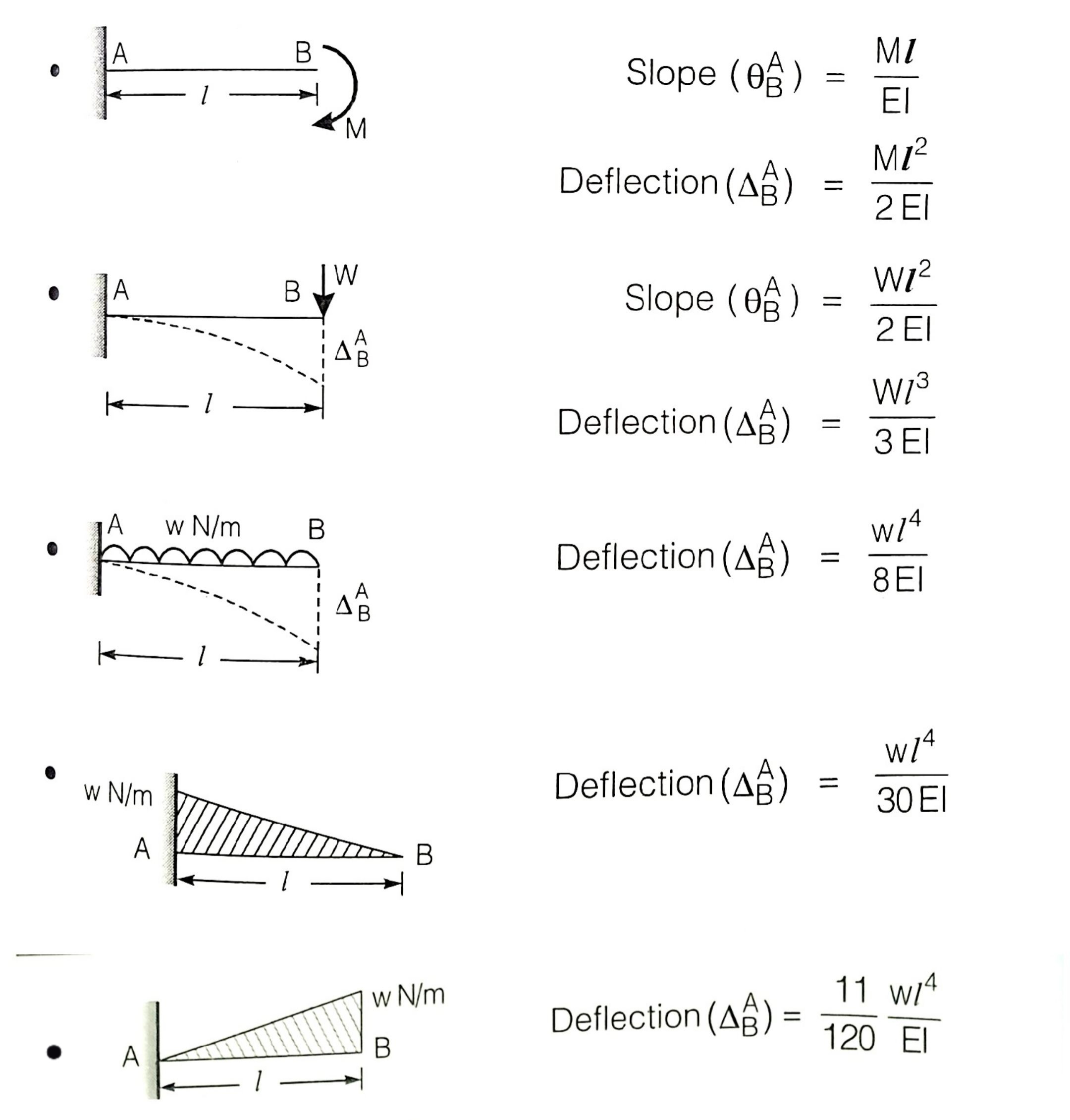
For simply supported beam

Beams of composite section
A composite section beam is described as a beam made up of multiple different materials, joined together so that they look and behave like a single piece, and the deflection that occurs in each piece is also equal.
The value of slope and deflection of a composite beam can obtain by algebraic addition of the flexural rigidities of the two or more different materials. Mathematically, it can be expressed in an equation as,
NOTE: The moment of inertia of a composite section can obtain about the centre of gravity of the section.
Common Mistakes
Students often get confused with Mohr's theorems in the moment area method and the conjugate beam method. But note that Mohr's theorems in both the deflection methods are different.
Context and Applications
This topic is significant in the professional exams for both graduate and postgraduate courses, especially for
- Bachelor of Technology in Mechanical Engineering
- Bachelor of Technology in Civil Engineering
- Master of Technology in Mechanical Engineering
- Doctor of Philosophy in Mechanical Engineering
Related Concepts
- Euler-Bernoulli theorem
- Structural Rigidity
- Superposition
Practice Problems
Q1. A beam of length l carries a uniformly distributed load of per unit length over its entire span. If its span is halved, then its slope will become? (Assume cantilever beam)
- half
- one-fourth
- one-eight
- one-sixteenth
Correct Option: (c)
Explanation: The slope of the cantilever beam having uniformly distributed load can be expressed as,
If the span is halved, then the slope of the cantilever beam can be given as,
Then, the slope will become one-eight of the original slope.
Q2. If the actual beam has both ends fixed, then the ends of the conjugate beam will be __________.
- fixed at both ends
- free at both ends
- fixed at one end and free at the other
- either 'a' or 'b'
Correct Option: (b)
Explanation: When the beam is fixed at both extreme ends, its slope and displacement will be zero. In contrast, the conjugate beam is free at both its extreme ends.
Q3. The width of conjugate beam is _________.
- 1/EI
- EI
- 2EI
- 4EI
Correct Option: (a)
Explanation: The width of the conjugate beam is equal to the reciprocal of flexural rigidity (EI). So, the width of the conjugate beam can be given as (1/EI).
Q4. With the help of conjugate beam method, we can find out the slope in case of ___________.
- cantilevers
- fixed beams
- simply supported beams
- both 'a' and 'c'
Correct Option: (c)
Explanation: The slope of the simply supported beams is evaluated with the help of conjugate beam methods. A simply supported beam has a hinge and roller supports if a conjugate beam has the same hinge and roller supports. Therefore, the conjugate beam method can be directly applied to simply supported beams.
Q5. The maximum slope of a cantilever is obtained when a point load acts at its ________.
- fixed end
- center of span
- free end
- none of these
Correct Option: (c)
Explanation: The slope of the cantilever beam having a point load P having flexural rigidity EI at the span of l can be expressed as,
So, the maximum slope of a cantilever carrying a point load at its free end.
Want more help with your mechanical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Slope and Deflection Homework Questions from Fellow Students
Browse our recently answered Slope and Deflection homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.