What is the meaning of stress?
The term stress indicates the measure of internal forces that develop due to an external force's application on an object. When a specific external force is applied to an object, internal stress generates in the material. The value of stress can obtain by taking the ratio of the externally applied force and cross-sectional area of the object. There are different types of stress depending on the type of external force.
What do you mean by stress transformation?
Whenever a body is under the presence of multiple external forces, there would be stresses that vary throughout the body, resulting in stress concentration. If there is a requirement to evaluate stresses regarding other coordinate systems that rotate with respect to original reference coordinates axes, then the stress transformation concept should be used.
The orientation of maximum principal normal stress, minimum normal stress, maximum shear stress, no shear stress, and pure shear stress in an object can be obtained by using the stress transformation equations.
Types of stress
Mechanical stress depends on the types of external forces that act on an object. There are different types of stress: tensile stress, compressive stress, shear stress, torsional stress, etc. Whenever a tensile force acts on a mechanical object, then there would be tensile stress generated in the object; and if a compressive force acts on the object, then there would be compressive stress generated in the object.
General state of stress
Generally, the state of stress at a point in the cube can be categorized into six independent normal shear stress components. These six states of stress components are given in the following diagram.
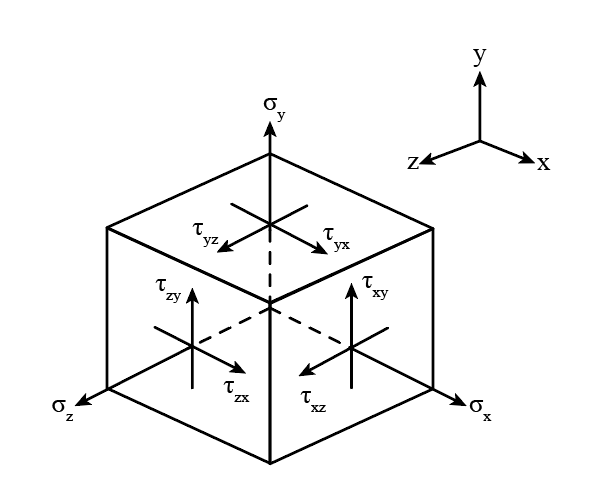
Here, represents the three normal stresses, and represents the three shear stresses.
Plane stress
Plane stress is stress in which two faces of the cubic element are free from stress. The state of plane stress can obtain in a thin plate subjected to forces at the mid-plane of the plate. General plane stress at a point in a two-dimensional mechanical element is shown in the following figure.
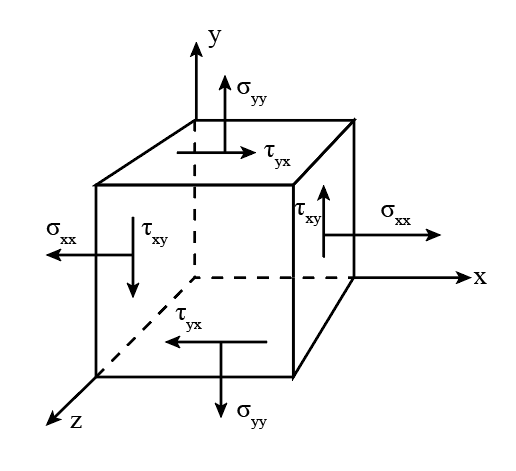
Here, represent the plane normal stress and represents the shear stress.
Sign convention
- Normal stresses that work in the positive co-ordinate directions on the positive face of an element would consider as a positive sign. In other words, stresses that act normally outwards to the face of an element is considered as positive and stresses that act in the negative co-ordinate direction on the negative face of the element would consider as a negative sign.
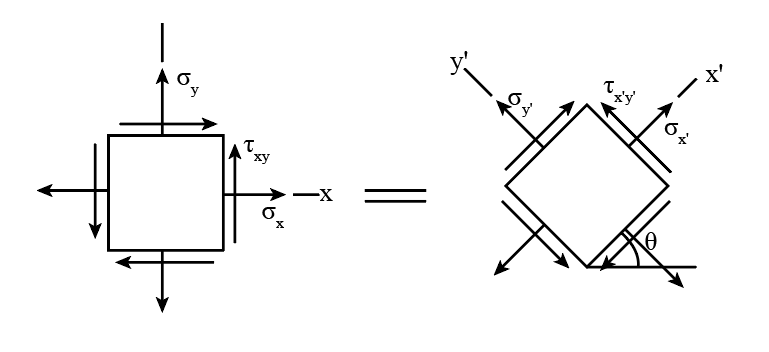
Plane stress transformation
A two-dimensional view of the element that can represent the relevant plane stress is given at the end of the section. If we rotate the elements of the point in different orientations, then different values of stresses would obtain. The stress components can transform from one orientation to another. The normal and shear stresses acting on the new elements are and respectively.
The general equation of plane stress transformation can be represented as,
Here, represents the angle of orientation of new element with respect to original reference co-ordinate.
Maximum and minimum principal stresses
To determine the maximum and minimum normal stresses, differentiate the expression of with respect to and set it equal to zero.
Here, represents the orientation of the principal planes that have two values and .
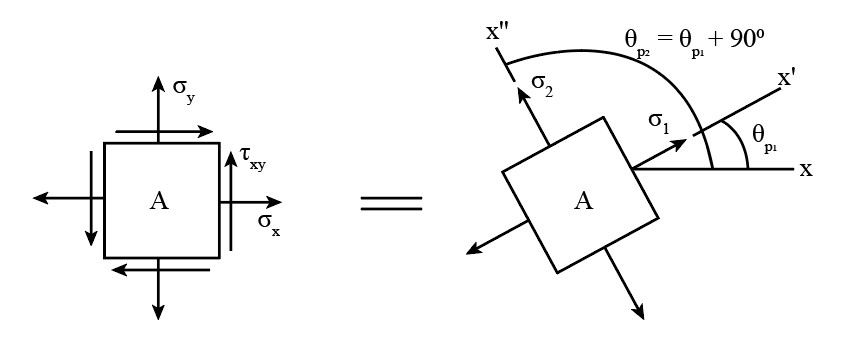
The expression of principal stresses that are maximum and minimum normal stresses can be represented as,
Here, represents the maximum principal stress and represents the minimum principal stress.
The value of maximum principal stress and minimum principal stress depends on the sign chosen. The set of these principal stresses refers to in-plane principal stresses, and the corresponding planes on which they act are referred to as principal planes of stress. On the plane of maximum and minimum principal stresses, the value of shear stress would be equal to zero, which means the plane of pure normal stress.
Maximum in-plane shear stresses
To determine the maximum shear stress, differentiate the expression of with respect to and set it equal to zero.
Here, represents the orientation of the maximum shear stress that have two values and .
The expression of maximum shear stress can be represented as,
Here, represents the maximum shear stress.
The maximum negative shear stress has the same magnitude but is opposite in sign. The plane of maximum shear stress would occur at to the principal planes.
The expression of the maximum plane shear stress can be represented as,
The plane of maximum shear stress also contains normal stresses. The value of normal stresses acting on the maximum shear stress plane can be determined with the help of different angle values.
Mohr's circle-plane stress
It is the transformation of plane stresses in the form of a circle that refers as Mohr's circle, a stress state in which all stresses are positive. The procedure of construction of Mohr's circle is given in the following steps.
- First establish a co-ordinate system between normal and shear stress.
- Plot the center of Mohr's circle on the -axis.
The expression of average normal stress can obtain as,
- Plot the reference point on the co-ordinate axis of the normal and shear stress.
- Now connect point with the center and becomes the radius of the circle.

The expression of the radius of Mohr's circle can be represented as,
Some important points regarding stress transformation
Some important points regarding stress transformation are given below.
- The value of principal stresses at a point represents the maximum and minimum value of normal stresses at that point.
- Whenever the state of stress is represented by the principal stresses, then no shear stress would act on the element.
- The state of stress at a point can also be represented in terms of maximum in-plane shear stress and, in the case of average normal stresses, also act on the body.
- The maximum in-plane shear stress represents from the element in principal stresses.
Common Mistakes
- Students may get confused about the difference between the plane of pure shear and the plane of maximum shear stress. However, normal stress does not exist on the plane of pure shear in an element, whereas it exists on the plane of maximum shear stress.
- Another point of confusion is related to the principal planes. However, on the principal planes, the value of shear stress equals zero, which means only normal stress exists.
- Students sometimes get confused about the sign convention of stress transformation. Always use standard international units to calculate principal stresses, maximum shear stress, etc. For example, tensile stress should be taken as positive and compressive stress should be negative.
Context and Applications
The topic of stress transformation is significant in the several professional exams and courses at undergraduate, Diploma, graduate, and postgraduate levels. For example:
- Bachelor of Science in Physics
- Bachelor of Technology in Mechanical Engineering
- Bachelor of Technology in Civil Engineering
- Masters in Technology in Mechanical Engineering
- Doctor of Philosophy in Mechanical Engineering
Related Concepts
- Strain transformation
- Stress tensor
- Strain tensor
- Principal plane
- Plane of pure shear
- Plane of maximum shear stress
- Mohr's circle
Practice Problems
Q 1. Which of the following options is correct about shear stress components on a three-dimensional object?
a. 4
b. 6
c. 5
d. 2
Correct answer: (b)
Explanation: In a three-dimensional object, the total number of stress components is nine, and out of nine, six are shear stress components, and the remaining three are normal stress components.
Q 2. Which of the following options is correct regarding the category of plane stress?
a. One-dimensional
b. Two-dimensional
c. Three-dimensional
d. None of these
Correct answer: (b)
Explanation: The term plane stress signifies a two-dimensional stress system in which two normal stress components and shear stress components exist according to two normal stress components.
Q 3. The value of shear stress on principal plane is
a. Zero
b. Maximum
c. Minimum
d. None of these
Correct answer: (a)
Explanation: The term principal planes signify the plane in an object at which the only normal stress exists. There would be no shear stress exists.
Q 4. The value of normal stress on the plane of maximum shear stress in an element is
a. Zero
b. Maximum
c. Not equal to zero
d. None of the above
Correct answer: (c)
Explanation: The term plane of maximum shear stress signifies a plane at which shear stress is maximum and normal stress also exists on this plane.
Q 5. Which of the following options is correct about total number of stress components on a three-dimensional object?
a. 4
b. 6
c. 5
d. 9
Correct answer: (d)
Explanation: In a three-dimensional object, the total number of stress components is nine, which represents a stress tensor matrix of nine elements.
Want more help with your mechanical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Stress transformation Homework Questions from Fellow Students
Browse our recently answered Stress transformation homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.