What is mean by torsion?
In mechanical engineering, torque, torsion, and twisting moment are three of the most important concepts which have different meanings. Torque is the consequence of a moment of a force that produces an angular acceleration in a body or induces rotational kinetic energy in a body. For instance, in an automobile, the power transmission shaft is a body that is always under rotation due to the external torque acting on it, this torque is created by the engine.
When the moment of a force tends to twist a body about its longitudinal axis, it is known as torsion. The twisting moment is the amount of resistance offered by the body due to twisting. A cantilever beam when acted by a concentrated torque at the free end, the beam experiences torsion. The amount of twisting moment thus induced in the beam depends on the magnitude of the torque applied at the free end.
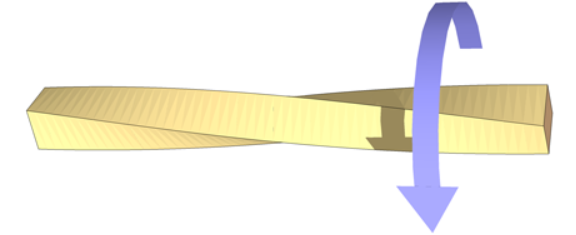
Torsion of circular shafts
Considering a solid circular shaft, this shaft will experience torsion if it acted by two equal and opposite torques (force couples) at the two ends. The force couples act parallel to the cross-section of the shaft and perpendicular to the longitudinal axis of the shaft. The nature of force couples is such that the magnitude and direction remain constant throughout the shaft.
Pure torsion
A circular shaft is said to be under pure torsion if the shaft is only acted by torques and twisting moments, whereas bending moments and axial forces remain absent. In practical working conditions, a shaft is under the action of combined loadings, under such circumstances, not all parts of the shaft are in pure torsion but a part of the shaft can be considered in pure torsion.
Stress distribution in pure torsion
When a solid circular shaft is under torsion, the internal structure of the material undergoes a shear. Due to this shear, shearing stresses are induced. The distribution of the shear stress is such that it varies along the radius of the shaft. For a typical solid circular shaft in torsion, shear stress is zero at the center of the shaft and maximum at the surface of the shaft.
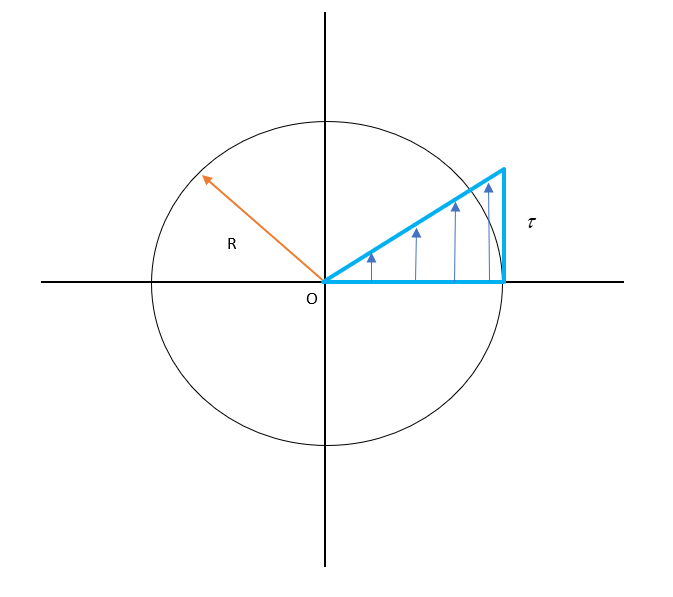
The above figure shows the shear stress distribution in a solid circular shaft. The shear stress is denoted by τ that varies linearly from the center O of the shaft having a radius of R.
Theory of pure torsion
The theory of pure torsion provides a mathematical relation between the shear stress-induced and the external torque acting on a body. This relationship is known as the torsion equation.
Certain assumptions are considered while deriving the torsion equation. The torsion equation is primarily derived for a body having a circular cross-section.
These assumptions are,
- The material of the shaft is considered to be homogeneous and this homogeneity is maintained throughout the length of the shaft.
- The shaft is assumed to be uniform through its length with a circular cross-sectional area.
- The twist experienced by the shaft is uniform.
- The cross-section of the shaft was assumed to be plain before and after torsion.
- There is no change in the length and direction of radial lines of the shaft before and after torsion.
- Induced stresses in the shaft under torsion are under the elastic limit of the shaft material.
Torsion equation
The torsion equation of a shaft of circular cross-sectional area is given by
Where is the external applied torque to the shaft
is the polar moment of inertia of the circular cross-section
is the shear stress induced in the shaft
is the radius of the shaft
is the shear strength of the shaft or shear modulus of the shaft
is the angle of twist of the shaft due to torsion
is the length of the shaft
Basic terminologies of torsion
Referring to the torsional equation introduced above, there are certain basic terminologies and concepts which are of immense importance in the the topic of torsion, some of the terminologies are outlined below.
Shear modulus or rigidity modulus, G
It is a measure of the rigidity of the shaft due to its material property to respond to shear deformation, i.e. torsion. Evaluating the ratio of shear stress with shear strain results in the modulus of rigidity. Its SI unit is Pascals, Pa. It is normally represented in higher units called, Giga Pascals, GPa.
Angle of twist,
The degree or amount of deformation induced in the shaft due to torsion is measured by the quantity known as the angle of twist. The angle of twist can be determined from the torsion equation, having known the external torque applied to the shaft, the shear stress-induced, the length and diameter of the shaft, and the shear modulus of the shaft. The angle of twist of a shaft under torsion is given by
The unit of angle of twist is usually measured in degree and radians.
Polar moment of inertia of shaft, J
The polar moment of inertia of the shaft is the measure of the resistance offered by the shaft due to deformation caused due to twisting. When the shaft tends to undergo a deformation caused due to rotation about one of its centroidal axes, the shaft resists this deformation by providing a counter-rotation that is equal in magnitude to the applied external rotation but opposite in nature.
The polar moment of inertia of a body having a circular cross-section is given by
, where, is the diameter of the solid shaft having circular cross-sectional area.
The unit of is .
Context and Applications
This topic finds its importance in different undergraduate and postgraduate degree courses like:
- Bachelors of Technology in Mechanical engineering
- Masters of Technology in Mechanical engineering
- Bachelors of Technology in Civil engineering
- Masters of Technology in Civil engineering
- Bachelors of Science in Applied Physics
- Masters of Science in Applied Physics
- Bachelors of Science in Applied Mechanics
- Masters of Science in Applied Mechanics
Practice Problems
Q1) Which of the following is the SI unit of shear modulus?
- N
- Nm
- Pa
- Kg
Answer: Option c
Explanation: The SI unit of shear modulus or rigidity modulus is Pascals, Pa.
Q2) Which of the following is true for induced shear stress in a solid circular shaft?
- Shear stress is zero at the surface and maximum at the center.
- Shear stress varies parabolically from the center of the shaft to the surface of the shaft.
- Shear stress is zero at the center and maximum at the surface of the shaft.
- All of these
Answer: Option c
Explanation: The shear stress distribution is linear for a solid circular shaft. It is zero at the center of the shaft and maximum at the surface of the shaft.
Q3) Which of the following quantities represents the resistance offered by the shaft due to deformation caused by external shaft?
- Moment of inertia
- Elastic modulus
- Polar moment of inertia
- Flexural modulus
Answer: Option c
Explanation: Polar moment of inertia indicates the amount of resistance offered by the shaft due to deformation caused by external torque.
Q4) Which of the following is the unit of polar moment of inertia?
Answer: Option d
Explanation: The correct unit of polar moment of inertia, , is .
Q5) Which of the following quantity is used to signify degree or amount of deformation undergone by shaft due to torsion?
- Shear modulus
- Polar moment of inertia
- Angle of twist
- None of these
Answer: Option c
Explanation: The degree or amount of deformation undergone by shaft due to torsion is given by angle of twist.
Want more help with your mechanical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Torsion Homework Questions from Fellow Students
Browse our recently answered Torsion homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.