What is Exponential Function?
The exponential function is a type of mathematical function which is used in real-world contexts. It helps to find out the exponential decay model or exponential growth model, in mathematical models. In this topic, we will understand descriptive rules, concepts, structures, graphs, interpreter series, work formulas, and examples of functions involving exponents.
Mathematical Definition of Exponential Function
An exponential function can be represented in form f(x) =ax, where x is the input variable. The graph of this function depends on the base of the function and the value of the x.
The mathematical representation of this function is,
f(x) =ax
Where a>0,
x = real number.
Here,
“x” is a variable and not a constant.
“a” is a base of exponent function and its value is always a constant.
An exponential curve decay or growth depends on the exponential function. The quantity that grows or decays by a fixed ratio (or fixed percent) at regular intervals is either exponential decay or exponential growth. The compound interest formula uses the exponential model to get the compound interest value of the function. The exponential function is always a one-to-one function.
Exponential Growth
In exponential growth, the quantity will grow slowly at the starting, and then quickly. The rate of change of exponential function will increase over time. The rate of growth becomes quicker as time passes. The ascent growth means an “exponential increase”. The formula to define the outline of exponential growth is:
Where r is the growth percentage, ‘a’ is the initial value and ‘n’ is a positive real number.
Exponential Decay
The magnitude of quantity decreases very quickly at first, and then slowly, in an exponential decay model. The rate of change of the value of the exponential function will decrease with the increase of time and it becomes slower as time increases. The quick growth means an “exponential decrease”. The mathematical formula of exponential growth is:
Where “r” is the decay percentage and “a” is again the constant initial value.
Graph of Exponential Function and Logarithm Function
The graph of the exponential function is as follows:
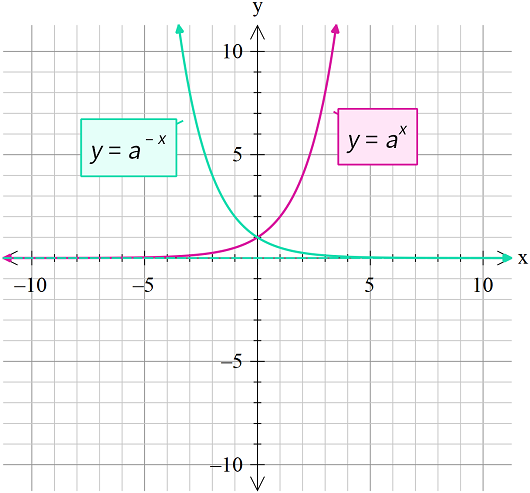
Here, as x increases, the function increases. But, the function decreases as x increases.
The exponential function which has a constant base of 10 is called a common exponential function. The expansions of the exponential function in the form of series is:
The range of the above series lies between 2 and 3 when x=1. When the base is e, the exponential function is called natural exponential function and it can be represented as ,
If and , the logarithm of x to base a is . Therefore, it is known as the logarithmic function. The graph of the logarithmic function is as follows:
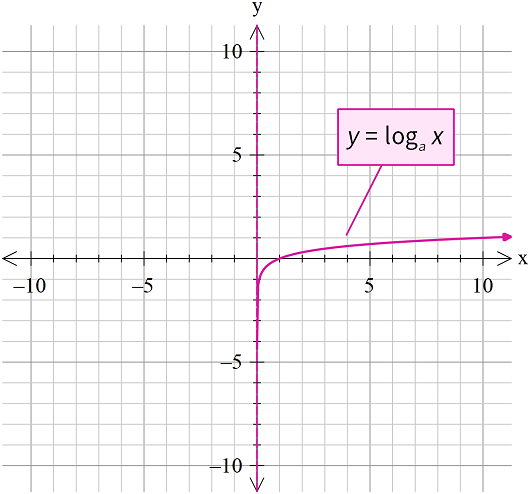
When base a = 10, then it is known as common logarithm and for the base a = e, it is known as natural logarithm and is represented by ln x. Some of the most important conclusion related to logarithmic functions which have a base a > 1 are as follows:
- The domain of the log function contains only a positive real number, but the logarithm of many functions may not be positive.
- For the log function, though the domain is from zero to infinity, the range is from negative to positive infinity (i.e. R).
- During the plotting of logarithm functions as we increase the value of variable x then the value of the function will also increase.
- The graph of the logarithmic function will never cut the y-axis, but it seems to tend towards it.
Derivative of Exponential Function
Now, we will calculate the differentiation (or derivative) of exponential functions.
The differentiation of exponential function, ex with respect to variable x is , i.e.,
From the above result, it can be observed the derivative of f(x) =ex has a special type of property, which means that the derivative of the exponential function, with base e, is the same as the original function.
Thus, there is no effect of differentiation on exponential function f(x) =ex.
Properties of Exponential Function
Exponential Function with Base Greater than 1
If the exponential function is represented by the equation, , then the graph of the function is shown as follows:
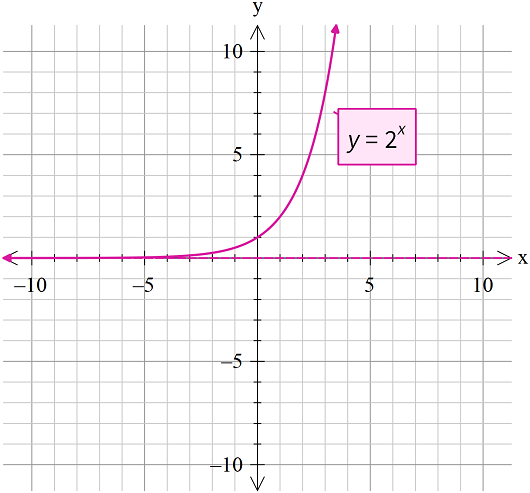
The properties of exponential function are:
- The curve of function will pass through the point (0,1).
- The range of an exponential function is .
- The nature of the graph is increasing means the value of the function will increase with the increase in the value of x.
- The graph of exponential function touches the x-axis at negative infinity it means the graph is asymptotic to the x-axis.
- The exponential graph is continuous and defined over its domain.
- At every point graph is smooth.
- The limit of the exponential function is defined as every point.
Exponential Function with Base Less than 1
If the exponential function is represented by the equation, , then the graph of the function is shown below.
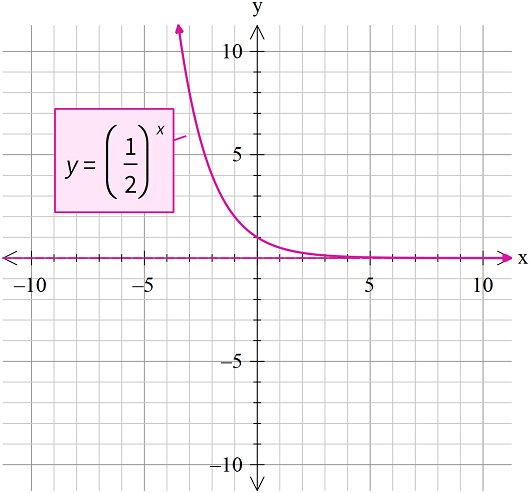
The properties of exponential function are:
- The curve of function will pass through the point (0,1).
- The range of the graph is from zero to infinity, i.e., .
- The nature of the graph is decreasing.
- The graph is continuous and defined over its domain.
- The limit of the exponential function is defined as every point.
- At every point graph is smooth.
Common Mistakes
- We can make a common error when finding the exponent value of expressions, for example, the square of 5x. So here the correct form is, (5x)2= 25x2. whereas the incorrect form is, square 5x is 5x2.
- Similarly, Square -5x. The correct form, (-5x)2= 25x2 and the incorrect form, square -5x= 25x2.
Formulas
If both a>0, and b>0, then some of the most important rules of exponential are:
We can simplify the exponent expression or solve the exponent equations using the following logarithmic formulas:
Here the base is a.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses,
- B.Sc. in Biology
- B.Sc. in Chemistry
- B.Sc. in Physics
- B.Sc. in Mathematics (Exponent equations and expressions)
- B.Tech.
- B.S.
- M.Tech
Related Concepts
Some of the related topics of growth functions and decay functions are given as:
- Exponential Decay
- Exponential Growth
- Chemical Kinetics
- Nuclear Physics
- Exponential equation
Practice Problem
Question:
Simplify and solve the exponential equation .
Solution:
Given:
Exponential equation: =0
When the base is the same:
Therefore, we can write
Thus, the LHS of given equation is written as:
Therefore, on simplification of the given exponential equation .
So, we have:
So, here the value of ‘x’ has no solution.
Want more help with your algebra homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Exponential Functions Homework Questions from Fellow Students
Browse our recently answered Exponential Functions homework questions.