What is a Kampyle of Eudoxus?
It is a curve studied with the classical problem of cube duplication. Here cube duplication, also called the Delian problem, is one of the geometric problems of antiquity that, given the length of the edge of a cube, asks the construction of a second cube such that its volume is twice the volume of the first. The only devices allowed for construction are the classic straightedge and compass.
Eudoxus was the first mathematician and astronomer who introduced astronomical mathematics to the world. Archimedes Eudoxus was the one who laid the foundation for the most advanced discussions in Euclid's Elements and builds a base building block for the study of surfaces and volumes by Archimedes.
Although most astronomers are assumed to have accepted his ample views in the middle of the 2nd century BCE, his assumption that every angelic motion is compatible and annular about the center endured until the time of the 17th-century astronomer Johannes Kepler. Dissatisfaction with Ptolemy’s modification of this assumption motivated abounding medieval and Renaissance astronomers, including Nicolaus Copernicus (1473–1543).
What is a Kampyle?
Kampyle is a pattern of quartic plane curves studied by the Greek mathematician and astronomer Eudoxus (from 408 BC to 347 BC) with the classical problem of doubling the cube.
- The word 'Kampyle' means a curve line or curve in Greek.
- This Eudoxus curve has an equation in Cartesian form as x4=a2(x2+y2).
- This curve has no solution at its origin. Thus, the domain and range of this function are all real numbers except zero.
- Its applications are studied in various fields like mathematics, physics, and engineering.
- Eudoxus also found the formula for measuring the pyramids, cones, and cylinders along with the elements of calculus with the study of the method of exhaustion.
Polar Form
The Cartesian equation can be written in terms of two parameters as
a2x4=b4(x2+y2), where a and b are integers.
The equation can be expressed in the polar form as
In this equation, there are two arbitrary constants a and b which affect the basic structure of this Kampyle. This means that if the values of a and b are changed, it will produce different graphs.
Let's assume a general Cartesian equation. In this equation when the value of a is increased, then the distance between the x-intercepts of the graph decreases.
Here in this example let assume the value of a is 1, and then increase the value of a.
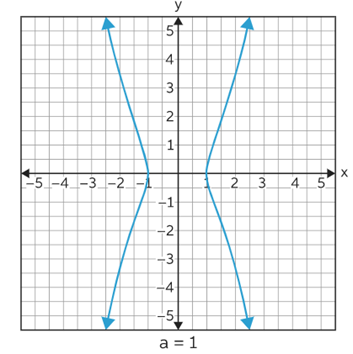
Now we have increased this value of a from 1 to 5.
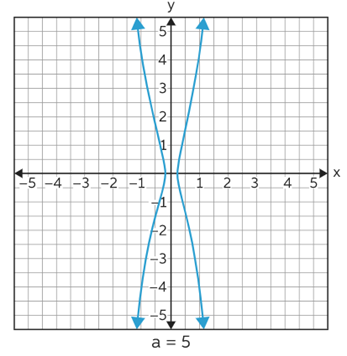
It is observed that the intercepts shifted toward each other or the width of the graph decreases.
Now come to the arbitrary constant b, since in polar form b and a are inverse and directly proportional to the curve r, so, the nature of b is just opposite to a. Thus, when the value of b is increased, the distance between the x-intercepts increases. This means that the width of the graph increases.
Let's see this with an example, let assume a graph of Kampyle of Eudoxus from the Cartesian form.
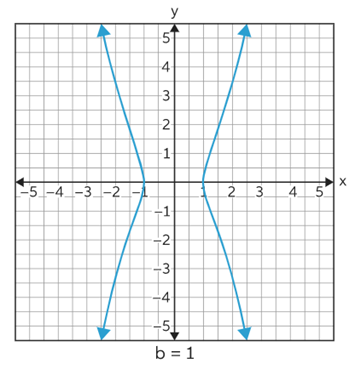
Now increase the value of b from b=1 to b=2.
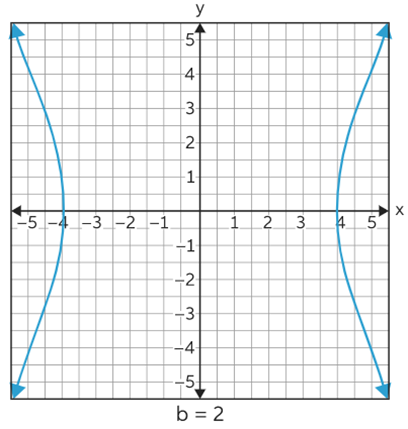
From above it can be concluded that when the value of b is increased the width of the graph increases.
Properties of the Curve
- The curve is symmetric about both x and y axes.
- The curve intersects the x-axis at and .
- Its inflection points are , one in each quadrant.
Parametric Form of Kampyle of Eudoxus
The parametric curves are those which are drawn with the help of parametric equations which differ from Cartesian equations. These are the curves that can't be plotted without using a single equation in terms of x or y.
In general, we have a function y=f(x) or x=f(y) having two variables x and y in the same equation. But in the parametric form, a third variable is used to make x and y in terms of only that third variable.
By this form, the coordinates of any curve are found separately just by knowing that third variable.
The parametric form of the equation x4=a2(x2+y2) is represented as:
Where .
The domain will also be changed as per the variable used. Hence, the domain of this
parametric form is , but the range will be the same as that of the function
x4=a2(x2+y2) as only the form of the function has changed.
Formula
The Cartesian equation of the Kampyle of Eudoxus is x4=a2(x2+y2).
The Cartesian equation x4=a2(x2+y2) can be written in the parametric form as
, where .
Context and Applications
The parametric form of the Kampyle of Eudoxus is widely used in physics, mathematics, and engineering.
Its application in kinematics in physics helps to find the trajectory of projectile motion.
The parametric curves in calculus are used in computer-aided designs.
This form is extremely helpful in determining the equations for two-dimensional and three-dimensional curves.
Related Concepts
- Kappa curve
- Deltoid curve
- Devil’s curve
- Bullet-nose curve
Want more help with your algebra homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Kampyle of Eudoxus Homework Questions from Fellow Students
Browse our recently answered Kampyle of Eudoxus homework questions.