What is Arc Length?
Arc length can be thought of as the distance you would travel if you walked along the path of a curve. Arc length is used in a wide range of real applications. We might be interested in knowing how far a rocket travels if it is launched along a parabolic path. Alternatively, if a curve on a map represents a road, we might want to know how far we need to drive to get to our destination. The distance between two points along a curve is known as arc length.
Arc of a Circle
Any part of a circle's circumference is considered an arc. To refresh your memory, a circle's circumference is its perimeter or the distance around it. As a result, we can assume that the circumference of a circle is the circle's full arc. The arc length in degrees is shown in the following figure:
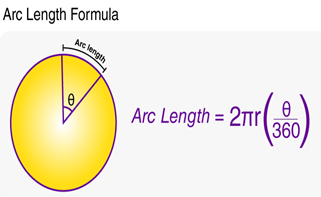
where :
θ is the central angle of the arc in degrees
r is the radius of the arc
π is read as Pi and its approximate value is 3.142
Types of Arcs
A circle may be divided into two arcs by a chord, a central angle, or an inscribed angle. The major arc is the greater of the two arcs.
Minor Arc
A minor arc is one that is not as large as a semicircle. The value of a central angle subtended by a minor arc is less than 180°. In other words, the minor arc is less than a semicircle in size and is defined by two points on the circle. The minor arc, for example, is arc AB in the circle below.
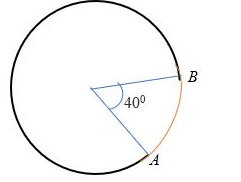
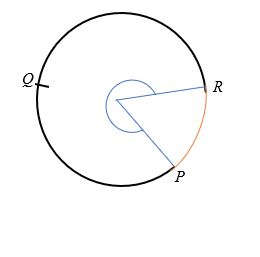
Major Arc
A circle's major arc is an arc that forms a greater than a 180-degree angle with the circle's base. The major arc is larger than the semi-circle and is represented on a circle by three points. The main arc of the circle shown below, for example, is PQR.
Arc Length Formula in Radian
The arc length formula is used to measure the length of the curved line that makes up the arc (a segment of a circle). In simple terms, the arc length is the distance that passes along the curved line of the circle that makes up the arc. It's important to note that the arc length is greater than the distance between its endpoints in a straight line.
The radius of a circle and the central angle define the length of an arc. We know that the arc length equals circumference for an angle of 360 degrees (2π). As a result, since the angle-to-arc-length ratio is constant, we can say:
L / θ = C / 2π
As circumference C = 2πr,
L / θ = 2πr / 2π
L / θ = r
We find out the arc length formula when multiplying this equation by θ:
L = r * θ
Hence, the arc length is equal to the radius multiplied by the central angle (in radians).
Arc Length Formula in Integral Form
Assume f is a continuous differentiable function on the interval [a,b]. Assume that f ' is a continuous differentiable function on the interval [a,b]. Let us calculate the length s of the curve on the interval, also known as the arc length over [a,b].
Arc Length & Sector Area
Area of a Sector- A sector is a segment of a circle surrounded by its two radii and the arc that links them. A semi-circle, which represents half of a circle, is the most common sector of a circle. A sector can be subdivided into two regions: a major sector and a minor sector. The major sector is OPBQ, and the minor sector is OPAQ, as seen in the diagram below. Since major and minor represent big and small, they are referred to as major and minor fields, respectively. There are no major or minor sectors in a semi-circle.
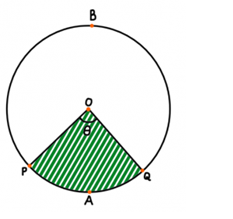
We realize that the diameter of a complete circle is 360 degrees. A circle's area is equal to π times the square of its radius length. If a sector of a circle with radius r scales, the area of the sector can be determined as follows:
Area of sector = (θ/360)×πr2
Length of an arc of a sector = (θ/360)×2πr
Trignometry-Arcsin
There is an inverse function for any trigonometry function that operates in the opposite direction. Such inverse functions have the same name as the originals, but with the word 'arc' added to the beginning. (The arcsin button on some calculators might be labeled asin or sin-1.) So arcsin is the opposite of sin, and so on. We understand "arcsin A" to mean "the angle whose sin is A".
For example, sin30 = 0.5 means that the sine of 30 degrees is 0.5 and arcsin0.5 = 30 means that the angle whose sine is 0.5 is 30 degrees. The word arc is used to denote the inverse function because the value of the inverse trigonometric function is dependent on the length of the arcs.
Arc Length and Curvature
The curvature of a smooth space curve shows how easily the curve bends or changes direction at a given point. A line, for example, must have zero curvature everywhere, while a circle (which bends in the same direction at all points) should have constant curvature. Curvatures should be smaller in circles with greater radii.
To calculate the curvature, we must first define the curve's direction at a given point. We can do this by using a curve's tangent vector that varies over time. To calculate the curvature, we must first define the curve's direction at a given point. We can do this by using a curve's tangent vector that varies over time.
Parameterization of Curve
Drawing a curve in space can be thought of as a function with a one-dimensional input and a multidimensional output. The input to such a function is known as a parameter, and the output is known as a parametric function.
You may need to find a parametric function that draws a specific curve in multivariable calculus. This is referred to as parameterizing the curve. We can solve problems of the parametric curves in calculus by using the arc length formula of line integral.
Common Mistakes
- Usage of substitution incorrectly.
- Indefinite integrals are handled incorrectly.
- Brackets that are unclear.
- Errors with square roots.
- Inequalities show signs.
Formula
- The formula for the length of the arc of a circle is , where r is the radius and is the central angle (in radians).
- The formula for the length of the arc of a circle is , where r is the radius and is the central angle (in degrees).
- The formula for the area of the sector of a circle is , where r is the radius and is the central angle (in degrees).
- The formula for the length s of a curve on the interval [a,b] is .
Context and Applications
- It is widely used in physics to study particle nature. It is used in a 2-dimensional figure's total arc length calculation (i.e. circumference); for example, a particle's 2-dimensional trajectory. Any physical quantities, such as energy or function, are proportional to the distance traveled. The arclength formula can be used to measure the distance traveled.
- When planning long flights, space flight engineers often use calculus.
- In mathematics, it is used to find a curve's slope.
- Calculating the area of every shape.
Related Concepts
- Mean value Theorem
- Definite integral
- Numerical Integration
- The curve on a surface
Want more help with your calculus homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Arc Length Homework Questions from Fellow Students
Browse our recently answered Arc Length homework questions.