What Are Conic Sections?
A conic section a curve that is formed when a plane intersects the surface of a cone.
The lateral surface of a cone is called a nappe. A double napped cone has two cones connected at the vertex. In the figure shown below, Cone 1 and Cone 2 are connected at the vertex. They form a double napped cone. The upper cone, that is the one above the vertex, is called the upper nappe, while the cone below the vertex is called the lower nappe.
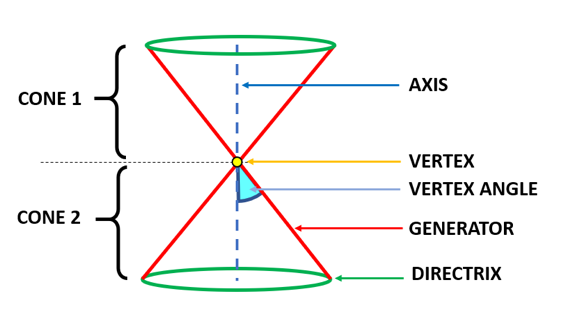
The perimeter of the circular base (shown in green) is called the directrix. A generator is a line that rotates around the vertex. The fixed line is called the axis. The angle between the vertex and the axis is called the vertex angle.
When a double napped cone (also called double right circular cone) is intersected by a plane at different angles with respect to its axis, we get different two-dimensional curves. These are called conic sections.
Classifying Conic Sections
Depending on the angle made by the plane with the vertical axis of the cone, four distinct shapes can occur:
Ellipse: When the plane intersects the double napped cone such that the angle between the vertex and the angle is greater than the vertex angle, the resulting conic section in the form of a closed curve is called an ellipse.
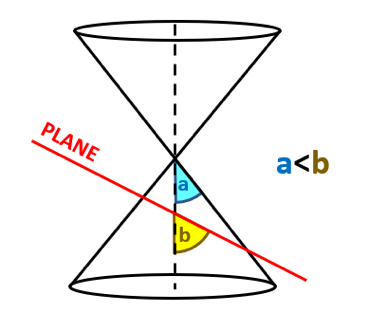
Parabola: When a plane intersects a double napped cone such that the angle between the vertex and the angle is equal to the vertex angle, the resulting conic section in the form of an open curve is called a parabola. When the plane is parallel to the generator, it results in a parabola.
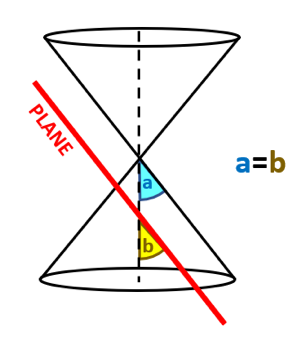
Hyperbola: When the plane intersects the double napped cone such that the angle between the vertex and the angle is less than the vertex angle, the resulting conic section in the form of an open curve is called a hyperbola. In a hyperbola, both the nappes of the cone are intersected, and the cutting plane is parallel to the axis of the double napped cone.

If the plane intersects the vertex of the cone, it results in a degenerate conic section.
Equations of Conic Sections
The general equation of any conic section is a second order, non-homogeneous equation in x and y:
Depending on the restrictions applied to the terms a, b, c, d, e, f, we can represent equations for different conic sections. All six coefficients need not be present in the equation for conics. However, for any given conic section, a, b, and c cannot be equal to zero simultaneously.
When given a second order equation and asked to identify the type of conic section, look for the product of coefficients a and c.
Case (i):
The conic section in this case is an ellipse.
Example:
The coefficient of ‘a’ here is 1, while that of ‘c’ is 4. The product of 1 and 4 gives a number greater than zero. Hence, the given curve represents an ellipse.
Case (ii):
The conic section in this case is a parabola.
Example:
The coefficient of ‘a’ here is 1 while that of ‘c’ is 0. The product of 1 and 0 returns a zero. Hence, the given curve represents a parabola.
Case (iii):
The conic section in this case is a hyperbola.
Example:
The coefficient of ‘a’ here is 1 while that of ‘c’ is -3. The multiplication of 1 and -3 gives a number less than zero. Hence the given curve represents a hyperbola.To summarize

Another parameter called eccentricity denoted by the letter ‘e’ can also be used to determine the shape of the conic sections. The value for eccentricity of different conic sections is listed below.
Graphing Conics
Ellipse:
An ellipse is a conical section in which the sum of distances from any point on the curve to two other fixed points is always a constant.
The general equation of an ellipse is
In the figure shown below, the total length of the orange line will always be equal to the length of purple line irrespective of where the point is placed on the curve. These fixed points are called foci of the ellipse. 
Hyperbolas and Parabolas of Conic Equations
Parabola:
- The focus of a parabola is a point about which it is constructed. Every parabola has one focus point at which reflected rays would converge. Thus, a parabola bends about its focus.
- Every parabola has a directrix. A point on the parabola has the same distance from the directrix as that from the distance between the point and the focus of the parabola.
- The point located between the focus and the directrix is called the vertex. A parabola turns around the vertex.
- Eccentricity of a parabola is always equal to 1.
A parabola with its vertex at (h, k) can be graphed in four different ways based on its symmetry about the x and y-axis with the respective governing equations.
(i) Parabola facing up 
(ii) Parabola facing down
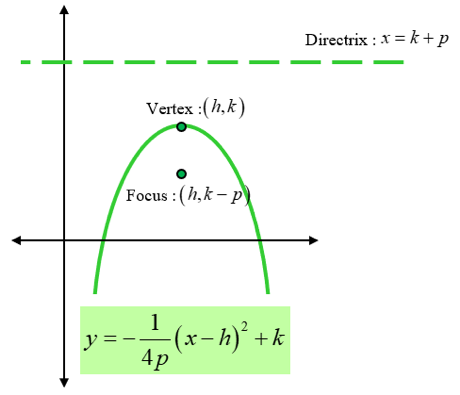
(ii) Parabola facing left
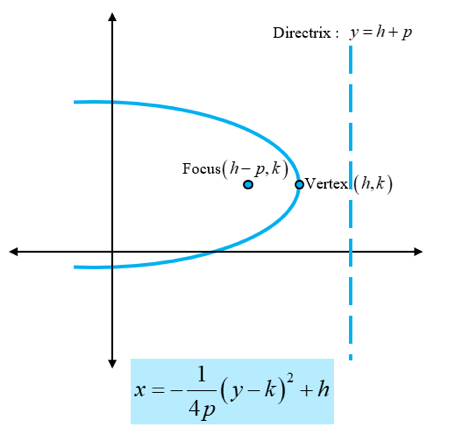
(ii) Parabola facing right
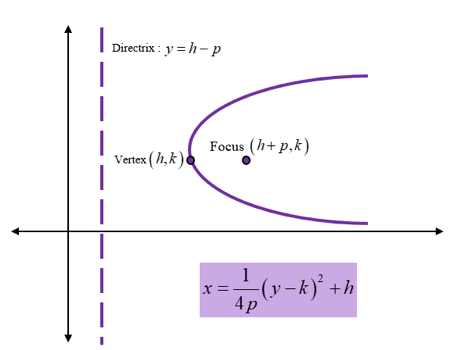
Hyperbola:
In a hyperbola, the difference of the distances between any point on the curve and two fixed points is always a constant. The two fixed points are termed as the foci of the hyperbola.
The general equation of a hyperbola is written as:
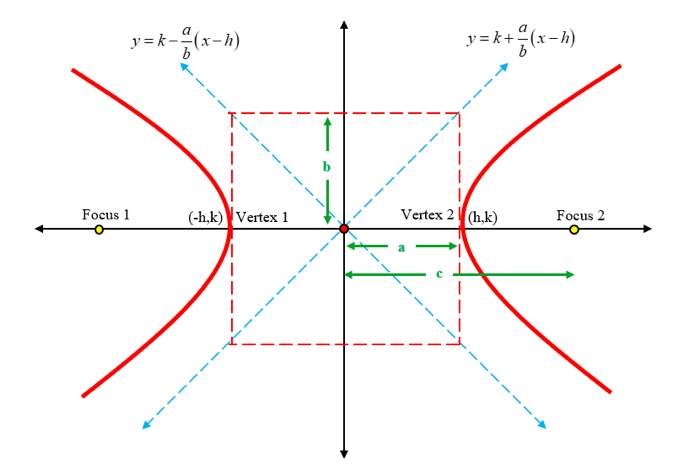
Conic Sections in Real Life
- The planets orbit around the sun in the shape of ellipses with the sun placed at one of the foci.
- Light beams are converged at the focus of the parabola using parabolic mirrors. Example: solar ovens, car headlights, spotlights, telescopes.
- The trajectory of an object thrown from the Earth’s surface follows a parabolic path. Hyperbolic as well as parabolic mirrors and lenses are used in systems of telescopes.
Hyperbolas in Real Life
- Astronomers predict adjustments to be made to the path of a satellite such that it gets to its destination using hyperbolic functions.
- Inverse relationships (when one quantity increases the other decreases) are depicted graphically using a hyperbola.
- Cooling towers of nuclear reactors have a hyperbolic structure.
- Radio system signals employ hyperbolic functions to identify geographic positions using hyperbolas. For example: LORAN.
Want more help with your geometry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.