What is Line Integral?

A line integral is one of the important topics that are discussed in the calculus syllabus. When we have a function that we want to integrate, and we evaluate the function alongside a curve, we define it as a line integral. Evaluation of a function along a curve is very important in mathematics. Usually, by a line integral, we compute the area of the function along the curve. This integral is also known as curvilinear, curve, or path integral in short. If line integrals are to be calculated in the complex plane, then the term contour integral can be used as well.     

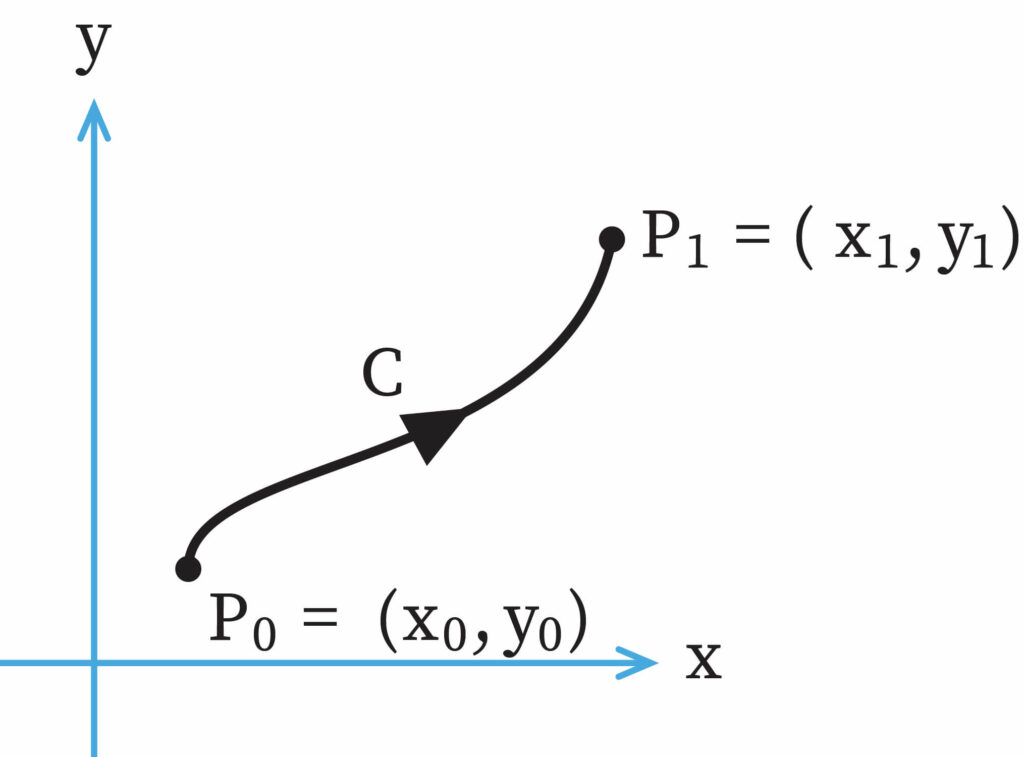
What is Line Integral in Calculus?

By definition, the integral where the integral function gets evaluated across the curve present in the coordinate system is called a line integral. Usually, we get two types of functions that are to be integrated in a line integral. These functions can be in the vector fields, or they can be in the scalar fields as well. It is possible to integrate these functions along the curve, whether they are vector-valued or scalar-valued. The variables in the functions are equated and the values are found out. When the value of all the points present on the vector field is calculated, then the obtained values can simply be added. This summation will help us to evaluate the line integral value.     

Fundamental Theorem of Line Integrals  

According to the fundamental theorem of line integrals, the path integral calculated in a gradient of a function is equal to the change in the value of the same function in its period of evaluation along the curve.

Mathematically, it can be written as ${\displaystyle {\int }_C\nabla f\cdot d\overrightarrow{r}}=f\left(\overrightarrow{r}\left(b\right)\right)-f\left(\overrightarrow{r}\left(a\right)\right)$, where C is smooth curve given by $\overrightarrow{r}\left(t\right)$ such that $a\le t\le b$ and $f$ is a function whose gradient vector is continuous on C.

This theorem evaluates the change in the value of the function as the function moves in the curve. This can be used in conservative vector fields. This theorem is the base on which the line integral applications work.    

How do Line Integrals Work?

Since the values are calculated in 2D planes, we need to assign the 3D plane values first. Without this extra variable, we cannot compute line integrals in 3D planes. In the graph, each point has a value. This value is considered to be the height if the function is represented in a 3D plane. We compute the line integral by considering this three-dimensional factor. When the line integral of a curve is calculated, we see that it is nothing but the area that is present under the curve in the defined field, and which has been traced above the surface.     

Formulas

The formula for a line integral is different in cases of the scalar fields and vector fields. They are as follows-     

Scalar Field     

For a scalar field, let us consider a function $f:S\subseteq R^n\to R$, where C is a smooth curve such that $C\subset S$. Then, the formula is- ${\displaystyle \underset{c}{\int }f\left(g\right)}ds={\displaystyle {\int }_a^{b}f\left[g\left(t\right)\right]}\left|g\text{'}\left(t\right)\right|dt$

The function $g:\left[a,b\right]\to C$ is considered to be an arbitrary parameter. Also, a < b, and the endpoints of C, are denoted by g (a) and g (b).

Vector Field 

We consider the function $f:S\subseteq R^n\to R$in a vector field, where C is a smooth curve such that $C\subset S$and it moves in the direction ‘g’. Then, the formula is- ${\displaystyle \underset{c}{\int }f\left(g\right)}dg={\displaystyle {\int }_a^{b}f\left[g\left(t\right)\right]}\cdot g\text{'}\left(t\right)dt$

The dot (.) represents the dot product in the above expression. Also, a < b, and the endpoints of C, are denoted by g (a) and g (b).     

Can Line Integrals be Negative? 

In short, line integrals can be negative. As the line integral value is independent of the parameterized drawing speed of the curve, the path produces tangent vectors that are in the opposite direction of the field vectors. Hence, the value of line integrals can be negative.     

Can Line Integrals be Zero?

In a scalar field, a line integral is usually not zero. However, if we are evaluating a closed loop in a conservative vector field, then the line integral can be zero. In such scenarios, the interpretation can result in special cases. For instance, if an object is moved along a specified path, and the line integral comes out to be zero, that means there was no work done for moving the object along the path in that field. This means that the direction of the work was not against the direction of the force field.         

Line Integral where C is a Circle  

When it comes to circular paths, the parameterization is naturally represented by either angle or theta. If we consider C to be a circle that has its center at (0, 0), or origin, then $\sqrt{x^2+y^2}=r$ can be considered as a constant throughout circle C. In such a case, the simplification of the integrand takes place. As a result, the integration is possible by direct parameterization methods.

What are the Applications of Line Integral?

There are many useful applications of line integral. The most common application includes the usage of line integrals for calculations of surface areas. This is especially useful when surface areas of 3D planes need to be calculated.     

Other than that, vector calculus comprises some major line integral applications. These include-     

• Wire mass can be precisely calculated with the help of line integral. 
• Alongside wire mass, the center of mass of the wire can also be calculated with a line integral.  
• Line integrals help in the calculation of moment of inertia. 
• Ampere’s Law uses line integral. It helps in evaluating the conductor and determining the magnetic field around it.
• Line integral is also used in Faraday’s Law of Magnetic Induction. The voltage generated in the loop can be calculated with a line integral. 
• When an object is displaced in a vector field, then the work done by the applied force can be determined with the help of a line integral.     

What is the Line Integral of an Electric or Magnetic Field?   

If we take an electric field that is in a closed-loop, then the line integral of the field is equal to the negative value of the rate of change of the magnetic flux, which takes place in the area of the enclosed loop. In the enclosed loop, the electromagnetic flux, or the emf or voltage generated is the value of the line integral. It is completely based on Faraday’s Law as stated above and electric generators work on this principle.          

How can we say Whether a Line Integral is Path Dependent or Not?  

 In general, if we can show that the gradient of a scalar field is the vector field itself, then the line integral can be said to be path-dependent.   

Context and Applications 

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for    

• B.Sc. in Mathematics     
• M.Sc. in Mathematics