What is Piecewise Function?
The group of one or more functions defined at different domains is known as a piecewise function. The rule of piecewise function is different for different pieces or portions of the domain.
Domain of a Piecewise Function
The domain of a function is the set of all possible x values of the function.
For example, amusing park ticket prices are different for different age groups. Thus the function for amusing park ticket prices would give a different value (ticket price) for each domain interval (age group).
| Amusing park ticket | |
| Age | Price ($) |
| 0-13 | 7.00 |
| 14-54 | 13.00 |
| 55+ | 10.00 |
Here, the domain of the function is separated into three intervals,[0, 14), [14, 55), [55,). It can be written as,
That is for the age group of 0 to 13 the value of the function is 7 or the function y=7 is used, for the age group of 14 to 54 the value of the function is 13, and for the age group more than 55 the value of the function is 10.
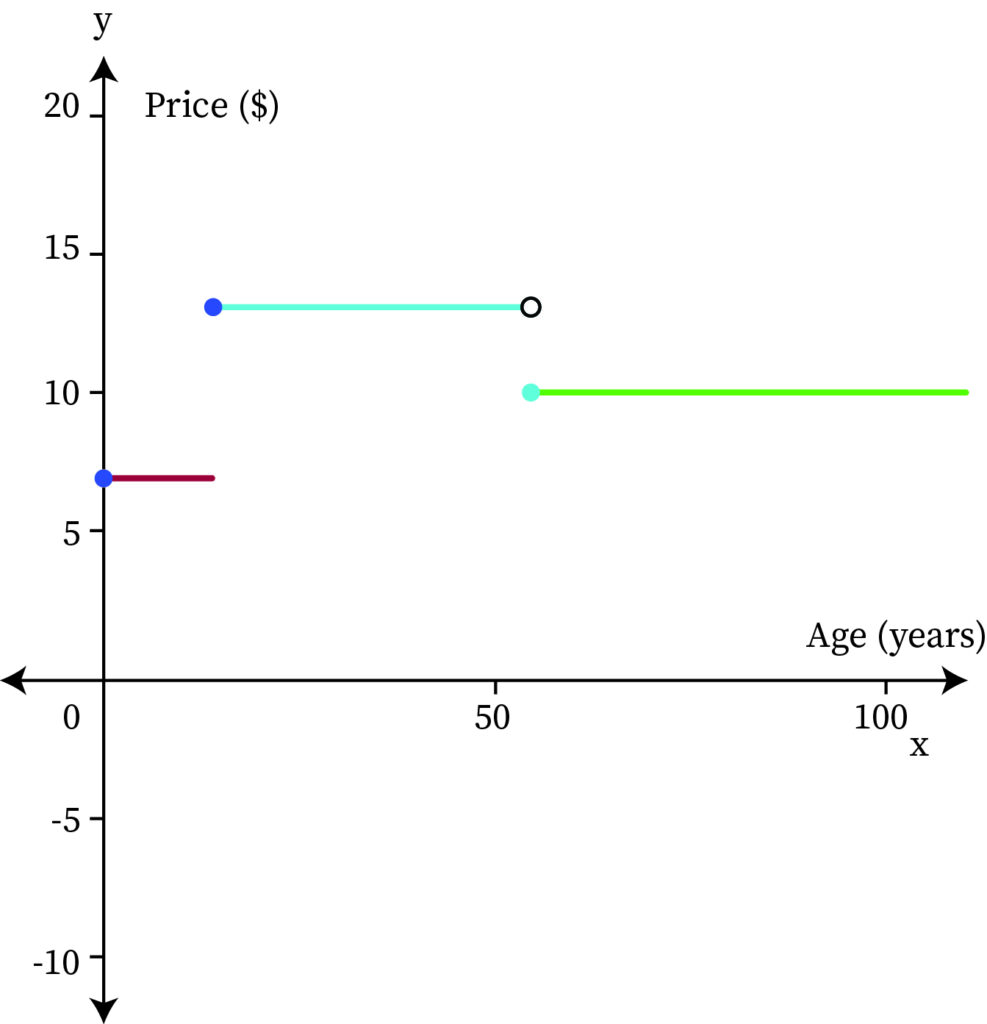
From the graph, the domain of the piecewise function is the set of all possible x values.
For example, the function .
The function f is a piecewise function. The function is defined with functions x2-2, x-2, and a constant function 8. Each of the function is paired with the intervals (-,0], [0, 10] and [10, ) respectively.
If you want to find f(x) for a particular value of x, first find which of the three intervals contain that particular value of x. After deciding on the exact interval, use the function paired with the interval to calculate f(x).
If you want to find f(5), first check, which of the interval has the value five. That is five belongs to [0, 10]. Use the corresponding function paired with the interval to find f(5).
Therefore, f(5) = 52 = 3
To find f(12), note that 12 belongs to [10, ). That means we should be seeing at the 3rd interval used in the definition of f(x), and the function paired with the interval is the constant function 8. Therefore, f(12) = 8.
Let’s find f(0). First, choose which of the three intervals used in the function f(x) contains the number 0. Notice that there’s some uncertainty at this point because 0 belongs to both the interval (-,0] and the interval [0, 10]. Whenever there’s uncertainty, choose any one of the intervals. Any of the functions that these intervals are paired with will provide you the same outcome.
That is, 02 -2=-2 is the same number as x-2=-2, so f(0) = -2.
Piecewise functions can be continuous (the graph above), or they can be discontinuous (contains breaks, jumps, or holes as in the graph below).
Note
If the value of y increases as the value of x increases, then the function is an increasing function.
If the value of y decreases as the value of x increases, then the function is a decreasing function.
If the value of y does not change as the value of x increases, then the function is a constant function.
Step Function
The step function is also a piecewise function that has a finite number of pieces. A piecewise function that is constant in each of the intervals such as amusing park tickets is known as a step function.
On the other hand, a function is called step function if for .
Properties
The main properties of step functions are given below:
- The addition or multiplication of two-step functions is also a step function.
- If a step function is multiplied by a number, then the result will be a step function. This shows that the step functions form an algebra over the set of real numbers.
- A step function can only take a finite number of values.
- Piecewise linear function is the definite integral of a step function.
Absolute Value
One of the piecewise defined functions in calculus is the absolute value function.
That is defined by:
The domain of the absolute value function is R. The range of the absolute value function is the set of non-negative numbers. The number |x| is called the absolute value of x.
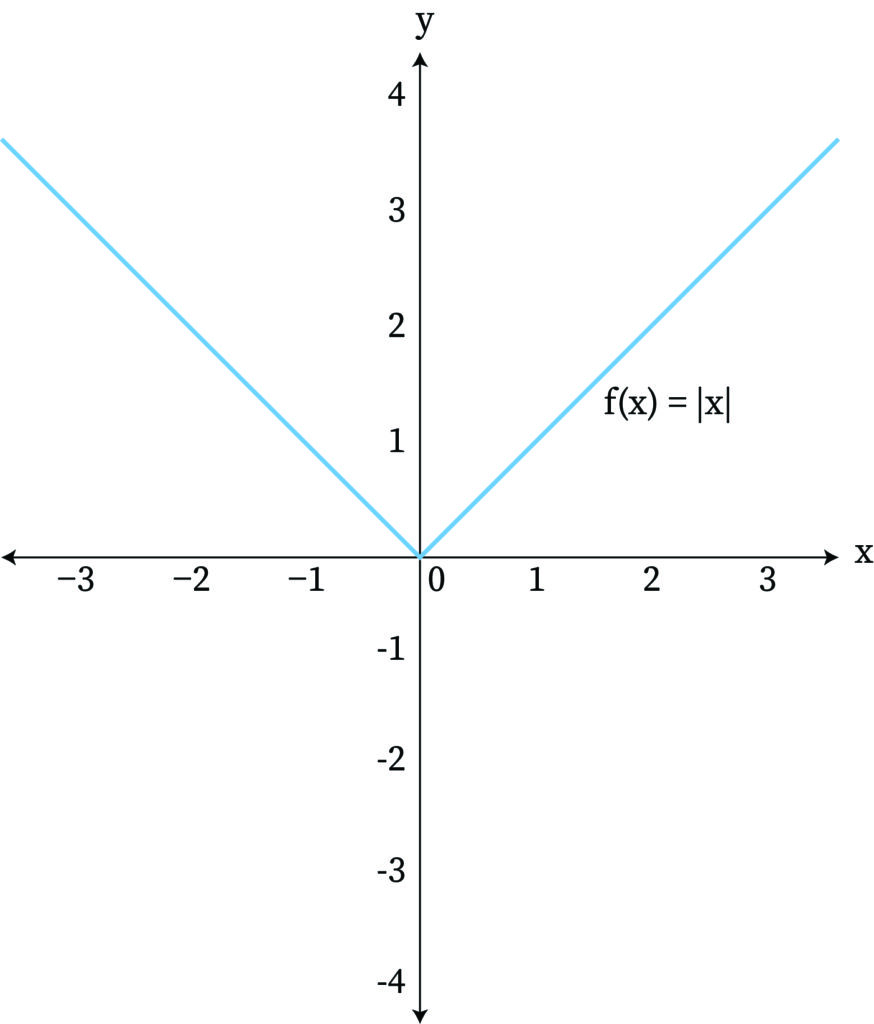
The graph of a piecewise function, which denotes an absolute value function, is "V"-shaped. This "V"-shaped graph is symmetric about a line, well-known as the axis of symmetry and it can open up or down.
- When a piecewise function graph denoting an absolute value function, opens up, then the function has a minimum value at its vertex.
- When a piecewise function graph denoting an absolute value function, opens down, then the function has a maximum value at its vertex.
Continuity and Differentiability of Piecewise Functions
The piecewise function f(x) is continuous a point x if and only if the left-hand right-hand limits of the functions exist and are equal to the value of the f.
(Or)
Let f(x) be a real valued function. Suppose that f(x) has a left limit S at x =a and a right limit R at x =a. Also f(x) is defined at x = a, and the values R and S are equal to f(a). That is,
If a piecewise function is continuous on a given interval in its domain it should satisfy the following conditions:
- The component functions are also continuous on the corresponding domain.
- There is no break at any endpoint of the domain within that interval.
If a piecewise function is differentiable on a given interval in its domain, it should satisfy the following conditions along with the above continuity conditions:
- The component functions are differentiable on the corresponding open intervals.
- The one-sided derivatives exist at all intervals endpoints.
- At the points where two subintervals touch, the corresponding one-sided derivatives of the two neighboring subintervals coincide.
Summary
- A piecewise function is a function where one or more function is used to define the output.
- The absolute value function is an example of a piecewise function.
- Piecewise function may be continuous or discontinuous.
- The piecewise function which is constant in each of the intervals is known as the step function.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- B.Sc. Mathematics
- M.Sc. Mathematics
Want more help with your calculus homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Piecewise Function Homework Questions from Fellow Students
Browse our recently answered Piecewise Function homework questions.