What are Vectors?
Vectors, in mathematics, are those quantities that tell us about the distance along with the direction whereas scalars are those quantities that tell us only about the length and not about the direction. The length in other words is called magnitude as it talks about the size.
What is the Difference between Scalars and Vectors?
Imagine you and your friend are asked to throw a ball as far as you can. It is your choice to throw it wherever you want. On scaling, it was found that your friend has thrown it a hundred meters away whereas you have thrown it 110 meters away. Since you have thrown with more velocity, the ball has reached far. Now you have won the match. There is no other instruction given to you. Now, this is a scalar quantity because it is about the magnitude.
But if someone asks you to throw the ball to the right side of where you are standing, you have to throw it in this particular direction with greater velocity to win the game. Here, not only the distance at which you throw the ball matters but also the direction in which it was thrown. This is a vector quantity.
In other words, scalars are represented by numbers whereas vectors are represented by numbers and direction.
What are Examples of Vectors?
Force is an example of vectors. It acts in some direction. The magnitude here would be the strength that is applied for pushing an object forward or pulling something backward. The velocity of a moving object tells about the speed at which the object is moving. Here, the magnitude is the speed. For example, the velocity of a car as the object moves in some direction. Thus, velocity is a two-dimensional vector quantity because velocity has both speed and direction. This can be represented as Cartesian coordinates with x coordinate and y coordinate representing the length and the direction.
The only vector which has no magnitude is the zero vector as it has no length. For this, the direction is not defined.
If the magnitude of a vector is one in some direction, then it is called a unit vector.
Is speed a vector? The answer is no because it only has magnitude. There is no direction for speed. So it is a scalar. Can you think of some more examples of scalars and vectors other than speed, force, and velocity? Is the height of an object a scalar or a vector?
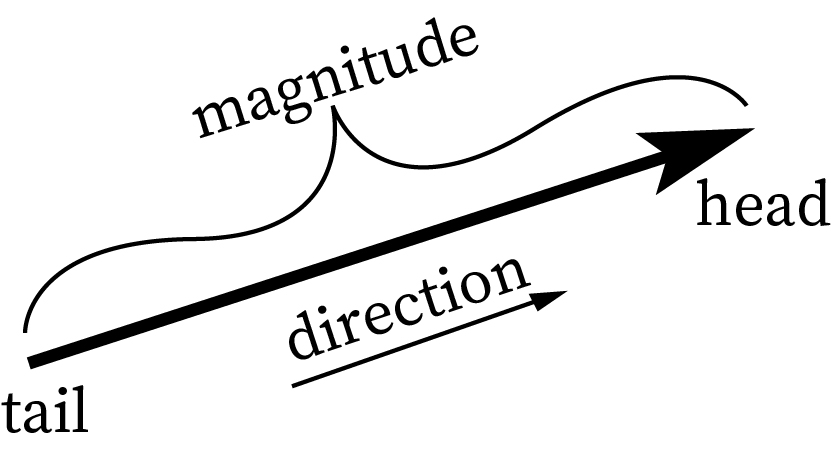
A vector starts at a point and ends in a point. It is shown as an arrow with a head and a tail. The tail of the vector is the starting point and the head is the ending point. It is represented as a directed line segment. The arrow shows the direction in which the objects move. If the arrow is at the right end of the line, the object moves towards the right side. If the arrow is at the left end of the line, the object moves towards the left side.
Position Vector
You might have a cone-shaped bell in schools with a rod inside it. As the rod bangs the sides of the bell, some sound is produced. The rod has one end fixed to the top and the other end oscillates. Suppose the rod is 15 centimeters long. As the rod moves, the vector will change in direction. It is a vector quantity as it has length and it can change in direction. It describes the position of the vector. Similarly, the length of a vector can change or both length and direction can changes.
Vector Addition
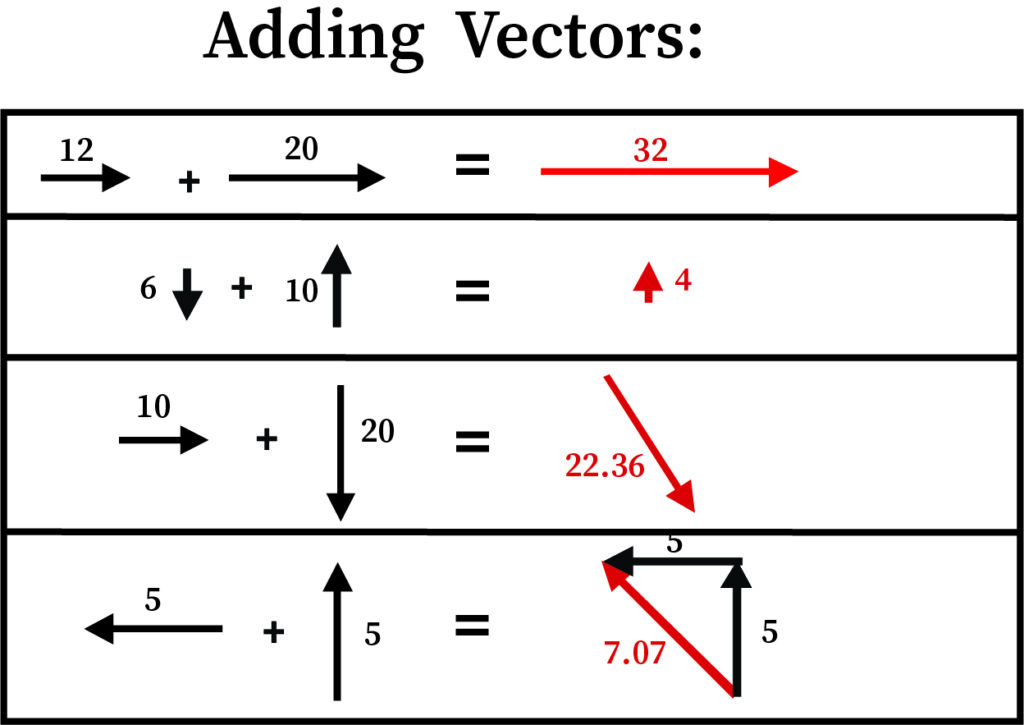
Suppose that your friend gives you the address to reach a library to take a text-book which is at point C. He instructs you to go 9 kilometers north to reach point B and 5 km east to reach point C from your home which is at point A. Now the two vectors are 9 and 5 given along with the direction. But drawing these points and joining the lines makes a right-angled triangle. What is the distance between points A and C? The Pythagorean theorem helps us to find this easily. How vectors are added?
Take the sum of the squares of the length and take the square root of the sum. The distance is 10.3 kilometers. The direction is measured using a protractor. Here, the direction is in angle. This method is called as a head-to-tail method for vector addition. The tail of A and the head of C is connected to form a new line and its length is calculated.
This is how vector addition is done.
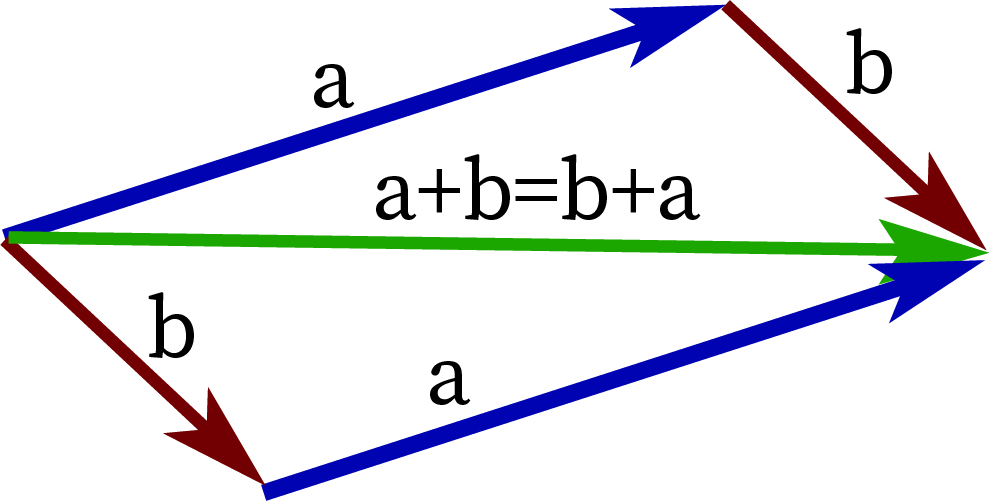
Note: The addition of vectors is commutative, i.e., the order of addition does not affect the sum of the vectors.
Subtraction of Two Vectors
Like vector addition, let us see vector subtraction. Suppose that you are going to the park and you meet your friend who is coming from the opposite direction. The opposite direction of a vector is considered to be a negative vector. Adding a positive vector and a negative vector gives the subtraction of two vectors.
In a real line, if you move to the left, the value of the numbers decreases. And, when you move to the right, the numbers keep increasing.
Vector Components
To solve a vector, we can split it as a horizontal component and a vertical component. As we saw the right-angled triangle above, consider the vector AC and break it as AB and AC. The horizontal component would be the component AB and the vertical component would be the component BC.
When are Two Vectors Parallel?
Suppose you are walking three times the distance your friend has walked in a straight road. If the distance you have covered is ‘a’ and the distance covered by your friend is ‘b’, then your distance can be written as multiplying ‘b’ three times. For example, 9 is a multiple of 3. That is, multiplying three times three gives 9. Then the vectors ‘a’ and ‘b’ are said to be parallel.
When are Two Vectors Perpendicular?
If two vectors form a right angle, they are said to be perpendicular. Their dot product is zero.
It is given by the formula . Here, is the magnitude of vector a, is the magnitude of vector b and is the angle between a and b.
Formula
The dot product of two vectors is evaluated as .
The cross product of two vectors is evaluated as .
Here, is the magnitude of vector a, is the magnitude of vector b, is the angle between a and b and is the unit vector perpendicular to both a and b.
Context and Applications
It is used in the K-12 curriculum, undergraduate and post-graduate mathematics and physics, and is asked in entrance examinations.
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelor of Science
- Master of Science
Want more help with your calculus homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Vectors Homework Questions from Fellow Students
Browse our recently answered Vectors homework questions.