What is meant by Angles in Circles?

Angles within a circle are feasible to create with the help of different properties of the circle such as radii, tangents, and chords. The radius is the distance from the center of the circle to the circumference of the circle. A tangent is a line made perpendicular to the radius through its endpoint placed on the circle as well as the line drawn at right angles to a tangent across the point of contact when the circle passes through the center of the circle. The chord is a line segment with its endpoints on the circle. A secant line or secant is the infinite extension of the chord.

Types of angles in a circle

Central angle

The angle in the center is an angle between any two radii. Diameter, the longest chord of the circle divides it into two equal halves and each center angle is 180⁰. The addition of the major, as well as the minor central angles of the segment, is always equal to 360 degrees inside a circle. The dimensions of the central angle corresponding to the measurement of the arc that both the sides cut out (intercepted arc) of the circle. To determine the central angle, the equation applied is

The measure of the angle = measure of its intercepted arc

Central angle = $\frac{Arc length x 360}{2\pi r}$

where '$r$' is the radius of a circle.

Inscribed angle

The inscribed angle is made between two chords that intersect on the circumference of the circle. It can also be the angle subtended at a point on the circle by any two other points on the circle. It is also the angle subtended by an arc on the opposite side of the circle. The angle subtended by the arc at the center is twice the angle subtended by the same arc on any other part of the circle.

Interior and Exterior angles

When the two lines intersect within the circle, an interior angle is produced with its vertex at the intersection point of the two lines and the sides of the angle are placed on the intersecting lines. The measure of the angle with its vertex within the circle is half the addition of the intercepted arcs.

To evaluate the interior angle, the formula used is

The measure of interior angle = ½ × (sum of intercepted arcs)

The angles whose vertex lies outside the periphery of the circle and the sides of the angle are tangents or secants of the circle are termed the exterior angle of the circle. The exterior angle contains its vertex at the junction of the two rays at the outward side of the circle. To measure the exterior angle of a circle, we need to equate it to half the difference of the measure of its intercepted arcs. The measure of any exterior angle is always equal to half the difference of the measure of its intercepted arcs. The equation is as follows:

The measure of the exterior angle = ½ × (difference of intercepted arcs)

Tangent Chord Angle

The tangent chord angle is the angle generated by the convergence of the tangent and the chord which comprises its vertex over the circle. The tangent chord angle is equal to half of the chord range.

Tangent chord angle = $\frac{Length of chord}{2}$

Inscribed Triangles

The inscribed polygon is the one with all the vertices on the circle itself which is called a circumscribed circle. Different shapes can be inscribed inside the circle, for instance, if a right-angled triangle is inscribed, then its hypotenuse is the diameter of the circle. Also, if both the inscribed angles of the circle intercept the similar arc, then the angles are said to be congruent. The angle opposite to the diameter of an inscribed right-angled triangle is referred to as 90 degrees.

Inscribed Quadrilaterals

The inscribed quadrilaterals correspond to the ones whose opposite angles are supplementary. After a quadrilateral is inscribed inside a circle, the interior angles sum up to 360 degrees, and both pairs of opposite angles add up to 180 degrees.

Properties of Angles

• The Inscribed angles which are subtended by the same arc are equal.
• The central angles subtended by the same length of arcs are equal.
• The angle at the center of the circle is twice any inscribed angle subtended by the same arc.
• The angle inscribed inside the semicircle is always 90°.
• An angle in between a tangent and a chord through the point of contact is equivalent to the angle in the alternate segment.
• The opposite angles of a cyclic quadrilateral are supplementary
• The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle of the circle
• A radius or diameter that is perpendicular to a chord separates the chord into two equal sections and vice versa.
• A tangent to a circle is perpendicular to the radius drawn at the point of tangency.
• When both the segments are made tangentially to a circle from the same point outside the circle, the segments have equal lengths.

Theorems of Angles in a Circle

Theorem 1: The angle subtended by a diameter or semicircle is a right angle on any point of the circle.

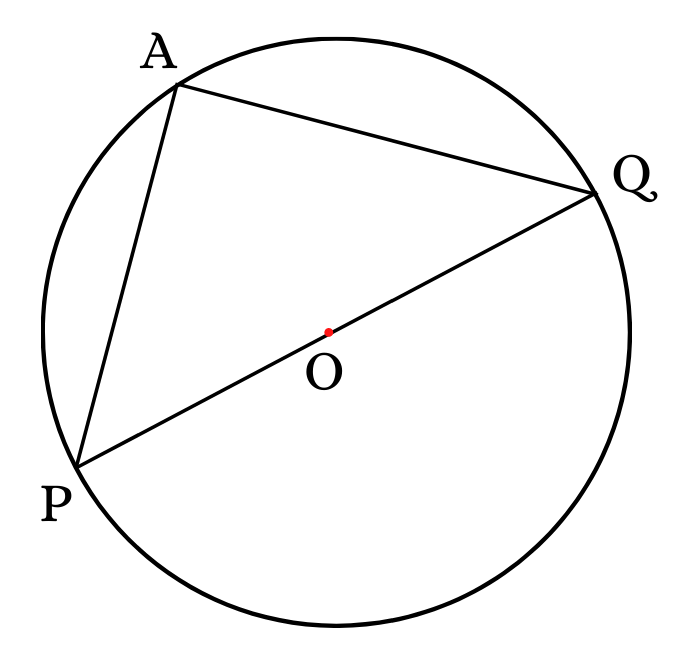
Given: A circle having center ‘O’, the diameter of the circle is PQ and it subtends the ∠ PAQ at the ‘A’ point on the circle.

Prove: That ∠ PAQ = 90°

Solution:

POQ is the straight line intersecting through the center of circle ‘O’.

So, the angle that is subtended by the arc PQ at ‘O’ is ∠ PAQ = 180° …………. (1)

According to the theorem of the chord of a circle, the angle subtended by an arc at the center is twice the angle subtended by it at any point on the remaining part of the circle.

Thus, ∠ POQ = 2 ∠ PAQ

∠ POQ /2 = ∠ PAQ

180°/2 = ∠ PAQ

Hence, ∠ PAQ = 90°

Theorem 2: The central angle is double of any inscribed angle subtended by the same arc.

Given: A circle having center ‘O’, the arc of the circle is PQ, it subtends the ∠ POQ at ‘O’ and ∠ PAQ at ‘A’ point of the circle.

Construction: Join AO and extend till ‘B’ point

Prove: The two cases are:

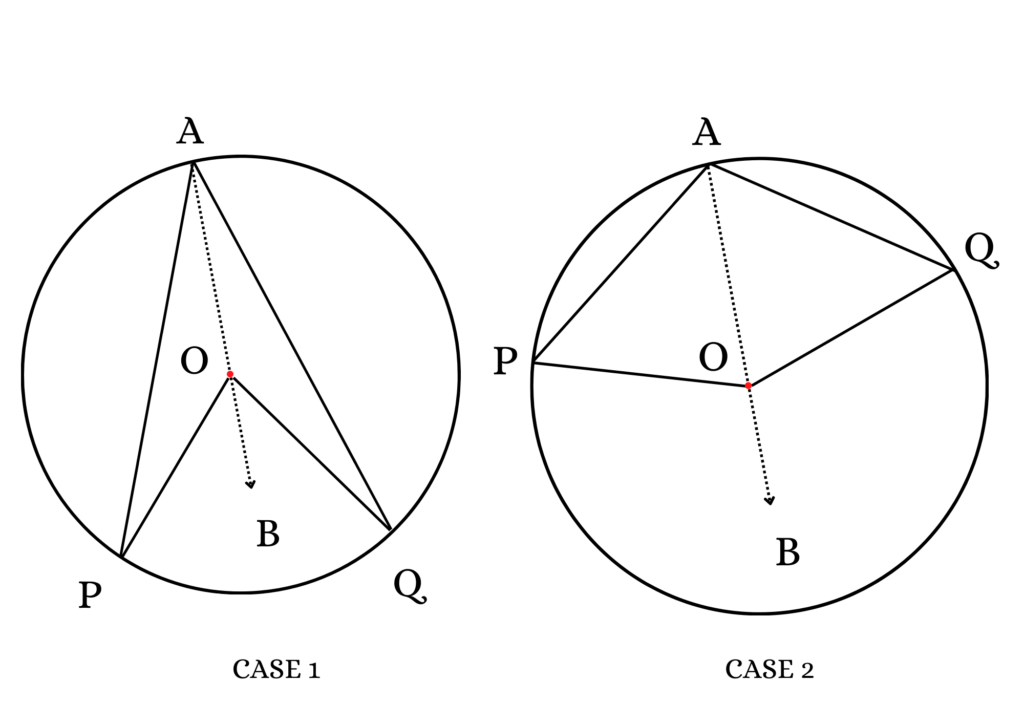
Solution (Case 1):

In △ APO,

OP = OA (Radius)

∠ OPA = ∠ OAP (the angles opposite to equal sides are equal in length) ………. (1)

Using the exterior property of angles which states that the external angle is the addition of interior opposite angles, we get,

∠ BOP = ∠ OPA + ∠ OAP

∠ BOP = ∠ OAP + ∠ OAP

∠ BOP = 2 ∠ OAP ………… (3)

In △ AQO,

OQ = OA (Radius)

∠ OQA = ∠ OAQ (the angles opposite to equal sides are equal in length) ………. (2)

Using the exterior property of angles which states that the external angle is the addition of interior opposite angles, we get,

∠ BOQ = ∠ OQA + ∠ OAQ

∠ BOP = ∠ OAQ + ∠ OAQ

∠ BOP = 2 ∠ OAQ ………… (4)

On summing up equations (3) and (4), we get,

∠ BOP + ∠ BOQ = 2 ∠ OAP + 2 ∠ OAQ

∠ POQ = 2 (∠ OAP + ∠ OAQ)

Hence, ∠ POQ = 2 ∠ PAQ

Solution (Case 2):

In △ APO,

OP = OA (Radius)

∠ OPA = ∠ OAP (the angles opposite to equal sides are equal in length) ………. (1)

Using the exterior property of angles which states that the external angle is the addition of interior opposite angles, we get,

∠ BOP = ∠ OPA + ∠ OAP

∠ BOP = ∠ OAP + ∠ OAP

∠ BOP = 2 ∠ OAP ………… (3)

In △ AQO,

OQ = OA (Radius)

∠ OQA = ∠ OAQ (the angles opposite to equal sides are equal in length) ………. (2)

Using the exterior property of angles which states that the external angle is the addition of interior opposite angles, we get,

∠ BOQ = ∠ OQA + ∠ OAQ

∠ BOP = ∠ OAQ + ∠ OAQ

∠ BOP = 2 ∠ OAQ ………… (4)

On summing up equations (3) and (4), we get,

∠ BOP + ∠ BOQ = 2 ∠ OAP + 2 ∠ OAQ

Reflex angle ∠ POQ = 2 (∠ OAP + ∠ OAQ)

Reflex angle ∠ POQ = 2 ∠ PAQ

Hence, 360° - ∠ POQ = 2 ∠ PAQ

Theorem 3: Different inscribed angles subtending the same arc are equal in length.

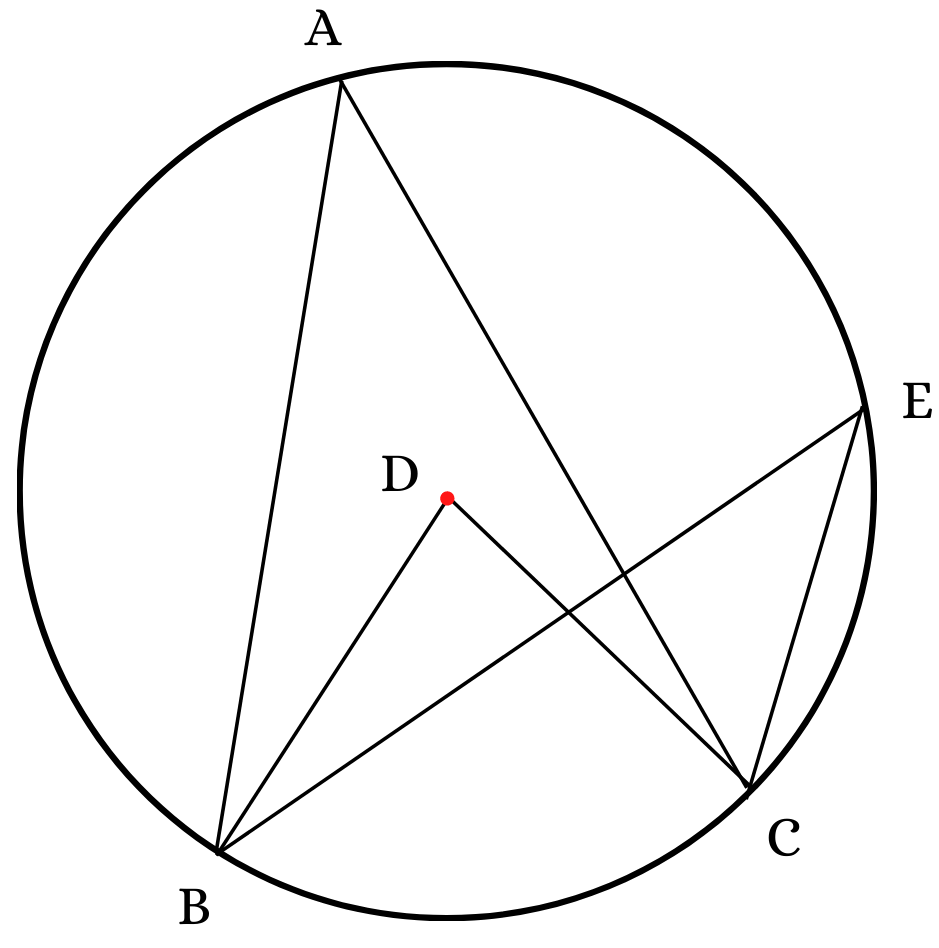
Given: Let ‘D’ point be the center of the circle ABC.

According to a property of the circle, the angle subtended by a certain arc at the center is twice the angle subtended by the same on any on the circumference of the circle.

Thus, using this, we get,

∠ BAC = ½ ∠ BDC

Also, ∠ BEC = ½ ∠ BDC

As both ∠ BAC and ∠ BEC are equal to half of ∠ BDC, we can say that,

∠ BAC = ∠ BEC,

Hence Proved.

Formulae used in Angles of a Circle

1. $Central Angle = \frac{Arc length \times 360}{2\mathrm{\pi r}}$
2. $Tangent Chord Angle = \frac{Length of chord}{2}$
3. $Inscribed Angle = \frac{1}{2}\times Intercepted angle$
4. $Interior Angle = \frac{1}{2} (sum of Intercepted angles)$
5. $Exterior Angle = \frac{1}{2} (difference of Intercepted angles)$

Context and Application

In real life too wherever we use circles or circular shapes, we need to do calculations based on angles in circles especially in architecture, engineering, and applied mathematics. This topic is studied in detail by students who undertake courses such as Bachelor of Technology (Engineering), Masters in Science (Algebra, Geometry, and Cryptography), and Masters in Science (Mathematics and Applications).

Related Concepts

• Apollonian circles
• Geometry of circles
• Inversion in a circle

Practice Problems

Q1. What type of angle is identified as a reflex angle?

1. Greater than 180°
2. Less than 180°
3. Equal to 180°
4. Not equal to 180°

Correct Option: a

Explanation: The type of angle identified as a reflex angle is greater than 180°. A minor central angle of the segment is always equal to 360 degrees inside a circle.

Q2. Which type of angle in the center is generated between two radii and its vertex is placed at the center of the circle?

1. Inscribed angle
2. Central angle
3. Exterior angle
4. Interior angle

Correct Option: b

Explanation: The type of angle in the center is generated between two radii and its vertex is placed at the center of the circle is the central angle.

Q3. In a cyclic quadrilateral, what is the nature of the opposite angles?

1. Equal to right angles
2. Equal to quarter angles
3. Supplementary  
4. None of the above

Correct Option: c

Explanation: In a cyclic quadrilateral, the opposite angles are supplementary.

Q4. Which of the following are the types of angles?

1. Central angles
2. Inscribed angles
3. Exterior angles
4. All of the above

Correct Option: 4.

Explanation: The types of arcs are central angles, inscribed angles, and exterior angles.

Q5. Which of the following statements are incorrect?

1. The angle at the center of the circle is twice any inscribed angle subtended by the same arc.
2. A tangent to a circle is perpendicular to the radius drawn at the point of tangency.
3. The Inscribed angles which are subtended by the same arc are unequal.
4. The opposite angles of a cyclic quadrilateral are supplementary

Correct Option: 3.

Explanation: The Inscribed angles which are subtended by the same arc are equal.