What Are Arcs in Circles?
A circular arc is the arc of a circle formed by two distinct points. It is a section or segment of the circumference of a circle. A straight line passing through the center connecting the two distinct ends of the arc is termed a semi-circular arc.
Length of an Arc
The distance between the two ends along a section of the curve is known as the arc length. Rectification of a curve involves evaluating the length of an irregular arc segment. If this curve results in a finite number (finite curve length), then it is called rectifiable.
The arc can be computed in two different ways. One is by measuring the angle of the arc, and the other is by measuring the arc’s length. The unit of measurement is centimeters for calculating the distance. The angle made at the center of the circle by joining the two endpoints of the arc is known as the sector (measured in degrees).
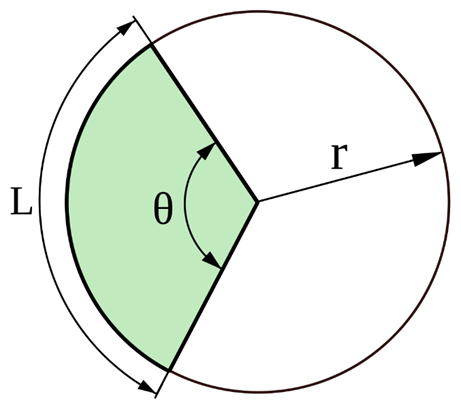
Components of a Circular Arc
Length
Where,
L = arc length,
=extended angle made from connecting the two ends of the arc,
= radius of the circle
Also, with respect to circumference, where, is the same as .
The length of an arc can also be calculated by graphically plotting two lines from the ends of the arc to the center of the circle, measuring the angle made when the two lines join, and then solving for the arc length using the formula (in degrees) =
Sector Area
The area of the sector (A) for a central angle () evaluated in degrees is
Segment Area
The area of the shape enclosed by the arc and the straight line between its two endpoints is
Radius
By using the intersecting chords theorem (secant tangent theorem), one can compute the radius of a circle () given the height (H) and the width (W) of the arc.
Formulae Used in Arcs of the Circle
Arcs of the Circle
In the below sentences, ‘’ represents the radius of the circle, ’d’ is the diameter of the circle, ’C’ is the circumference of the circle, ’L’ or ‘s’ is the length of an arc of the circle, and ‘’ is the angle which the arc subtends at the center part of the circle.
For a circular arc,
For a semi-circular arc,
For an arbitrary circular arc:
If is in radians, then
If is in degrees, then
If is in grads, then
If is in turns, then , where 1 turn is one complete rotation around the circle.
Great Circles on Earth
The nautical mile and the meter (or kilometer) are the two units of length that were previously termed such that the arc lengths of large circles on the Earth’s surface would easily associate with the angles they make at the center numerically. The equation under the following conditions:
If ‘s’ is in nautical miles and ‘’ is in arcminutes ( degree)
If ‘s’ is in kilometers and ‘’ is in centigrade ( grad)
The distance ranges were selected so that the Earth’s circumference becomes equal to 40,000 kilometers or 21,600 nautical miles, which are the corresponding angle units in a single entire rotation.
Types of Arcs
An arc is a section or segment of the circumference of a circle. A straight line that can be produced by joining the two terminal points of the arc is known as a chord of a circle. If the length of an arc is precisely half of the circle, then it is known as a semi-circular arc. Each pair of endpoints on a circle either generates one minor arc and one major arcs, or two semicircles. When the endpoints are that of a diameter, the circle is divided into semicircles. The various types of arcs in a circle include:
- Minor arc: An arc that will subtend an angle at the central portion of the circle which is less than 180 degrees or π radians. Minor arcs are related to less than half of the rotation of the circle.
- Major arc: An arc that will subtend an angle at the central portion of the circle which is more than 180 degrees or π radians. Major arcs are related to more than half of the rotation of the circle.
- Semi-circular arc: An arc associated with exactly half of a rotation (180°) out of the entire circle (360°).
- Meridian arc: A curve between two ends on the surface of the Earth having the same longitude. A meridian arc may indicate either a segment of the meridian or its length. The reason behind measuring meridian arcs is to find a figure of the Earth. Multiple computations of the meridian arcs are useful to create the reference ellipsoid structure. The dimensions of the meridian arcs at various latitudes along several meridians across the globe can be merged for approximating the geocentric ellipsoid which could fit the whole world. Technology uses the Astro-geodetic method of evaluations as well as satellite geodesy methodologies to find reference ellipsoids, which are then a great help for global coordinate systems like WGS 84.
Context and Applications
Several arc properties are useful in the Archimedean spiral and its arc length, cycloid and its arc length, ellipse and its arc length, helix and its arc length, parabola and its arc length, sine and cosine and its arc length, and triangle wave and its arc length. This topic is studied by students who undertake courses such as Bachelors of Engineering, Masters in Science (Geographical Systems), and Masters in Science (Geoinformatics).
Related Concepts
- Earth’s Arc
- Geographical Information Systems
- Spatial analysis
Practice Problems
1. What is meant by an arc of a circle?
- Arc drawn between two points
- Arc outside circle
- Arc on the circumference
- None of the above
Answer: a
Explanation: An arc of a circle is the arc drawn between two points. It is the section or segment of the circumference of a circle. A straight line passing through the center connecting the two distinct ends of the arc is termed a semi-circular arc.
2. An arc can be measured by______________________.
- Measuring the length of the arc
- Measuring the angle of the arc
- Measuring the length and angle of the arc
- Measuring its distance from the center
Answer: c
Explanation: An arc is measured by measuring the length and angle of the arc. The unit of measurement is centimeters for calculating the distance. The angle made at the center of the circle by joining the two endpoints of the arc is known as the sector (in degrees).
3. What is the circumference of Earth (in nautical miles)?
- 40,000
- 21,600
- 32,000
- 56,000
Answer: b
Explanation: The circumference of Earth is 21,600 nautical miles.
4. Which of the following are types of arcs?
- Major and minor arcs
- Semi-circular arcs
- Meridian arcs
- All of the above
Answer: d
Explanation: The types of arcs are major and minor arcs, semi-circular arcs, and meridian arcs. Each pair of endpoints on a circle either generates one minor arc and one major arc, or two semicircles. When the endpoints are that of a diameter, the circle is divided into semicircles.
5. Which of the following statements are incorrect?
- Minor arcs are related to less than half of the rotation of the circle.
- Major arcs are related to more than half of the rotation of the circle.
- Semi-circular arcs are associated with exactly half of a rotation (180°) out of the entire circle (360°).
- Meridian arcs are the curve between two ends on the surface of the Earth having different longitudes.
Answer: d
Explanation: Meridian arcs are the curve between two ends on the surface of the Earth having the same longitude.
Want more help with your geometry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Arcs in Circles Homework Questions from Fellow Students
Browse our recently answered Arcs in Circles homework questions.