What is Congruency?
“Congruency” is used extensively in geometry. It defines the relationship between two 2-D or 3-D objects that are congruent. In this section, we will discuss when two objects can be congruent and how the congruency can be shown mathematically.
What are Congruent Objects?
The objects with the same shape and same size are said to be congruent to each other. In simple terms, if we take an object and superpose the object on a second object, it will cover the second object completely, if the two objects are congruent.
Are these smileys congruent to each other?

If we place the first smiley on the second one, they fit each other perfectly. Hence, we can say that both these smileys are congruent to each other.
We can also say that two objects will be congruent to each other if we cut one object and fit it into the second object and the edges of the first object align with the second one completely.

Let us take 2 circles of different shades. We would like to see whether these circles are congruent. We have cut the blue-shaded circle into halves. We take one half and superpose it on the green shaded circle. We can see that the edges have aligned perfectly and therefore we can say that both the circles are congruent to each other.
Therefore, we can say that congruency is the relation between two 2-D or 3-D objects that are congruent.
Two objects are said to be congruent when they have the same shape and size. When we take one object and superpose it on a second object and if it covers the second object completely, without having to make any changes, like bending, twisting, or stretching, in either object, then both the objects are said to be congruent.
What are Two Congruent Shapes?
Congruence can be found in any figure, such as in geometry among line segments, angles, triangles, and so on.
Let us see how we can determine if two objects are congruent.
Congruence of Plane Figure
As we have already learned, we can use the method of superposition on any figures of the same size and shape to determine whether they are congruent to each other.
Congruence among Line Segments
Line segments of equal length are said to be congruent.

Here, .
Its converse is also true. That is, we can say that two congruent line segments have the same length.
Congruence of Angles
Two angles with equal measurements will be congruent to each other.

Here, , so .
Congruence of Triangles
Two triangles having the same shape and size that cover each other perfectly when superposed on each other are said to be congruent to each other.
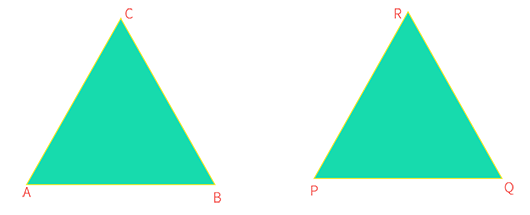
In the above figure, we can see that and have the same shape and size.Hence, .
As we explore these two triangles in more detail, we can see that when is superposed on ,
vertices P, Q, and R will coincide with vertices A, B, and C, respectively. Similarly, all the corresponding angles and sides of both the triangles will coincide.
From the above example, we can conclude that when two triangles are congruent to each other, their corresponding angles and sides are also congruent to each other. This is called the CPCT theorem. In simple terms, corresponding parts of congruent triangles are equal and congruent.
Congruency Rules for Triangles
Two friends Jack and Jill learned about triangles recently. Jack showed Jill and tells her to draw a similar one. He says that he will provide some information about to Jill, based on which Jill needs to draw that is congruent to .
Jack specifies the length of .
Jill replies that she can draw more than one triangle (shown in the below figure) with this information and therefore she needs more information to draw a congruent triangle.

Side-Side-Side Congruence
When Jack specifies the lengths of and as well, Jill draws the that is congruent to .
Given .
It gives .

The above congruence is called SSS, i.e. Side-Side-Side, congruence. This congruence states that two triangles with three equal corresponding sides are congruent.
Side-Angle-Side Congruence
Now, Jill tells Jack that she does not need the length of the third side. Instead, she wants to know the measurement of the angle included between the other two sides.
Now, Jack tells her the lengths of and , and the measurement of . Again, Jill draws that is congruent to .
Given .
It gives .
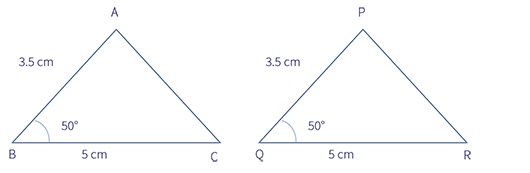
The above congruence is called SAS, i.e. Side-Angle-Side, congruence. This congruence states that two triangles are congruent if any of their two corresponding sides and the angle included between them are equal.
Angle-Side-Angle Congruence
Now, Jill tells Jack to specify the length of only one side and the measurement of the two angles that include the given side. Jack tells her the length of and the measurement of and . Again, Jill draws the that is congruent to .
Given .
It gives .
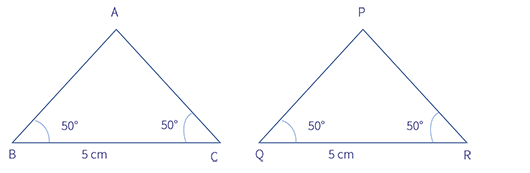
The above congruence is called ASA, i.e. Angle-Side-Angle, congruence. This congruence states that two triangles are congruent if any of their two corresponding angles and the side included between them are equal.
Now, Jack tells Jill that she cannot know the length of her preferred side anymore. Instead, Jack gives her the measurement of two angles and the length of one non-included side. Jill uses this information to draw the that is congruent to .
Given .
It gives .
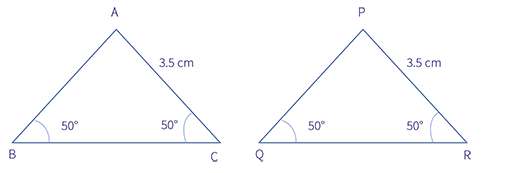
The above congruence is called AAS, i.e. Angle-Angle-Side, congruence. This congruence states that two triangles are congruent if any of their two corresponding angles and one corresponding side are equal. This is a modified version of the ASA congruence. We can use the given information to find the measurement of the angle which is not given by using the measurement of all the angles and ASA congruence.
Right Angle-Hypotenuse-Side Congruence
Now, Jill tells Jack that it is also possible to draw a congruent triangle with only two known sides, but the triangles should be right-angled.
Given .
It gives .
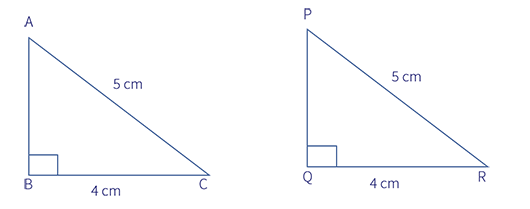
The above congruence is called RHS, i.e. Right angle-Hypotenuse-Side, congruence. This congruence states that two right-angled triangles are congruent if their corresponding hypotenuse and any other corresponding side are equal.
Technical Language/Glossary
- SSS: Side-Side-Side
- SAS: Side-Angle-Side
- ASA: Angle-Side-Side
- AAS: Angle-Angle-Side
- RHS: Right angle-Hypotenuse-Side
Context and Applications
We have already seen through various examples how congruency works.
- In the real world, congruent triangles are used in architecture, specifically in the construction of bridges and symmetrical bodies.
- Manufacturing wheels of a bicycle, motorbike, or any other vehicle also requires the application of congruency.
- Even the human body is made up of congruent parts like the fingers of both hands.
- Many daily used objects like pages of a book, similar products of the same company, etc. are examples of congruency.
Common Mistakes
Some of the possible common errors that occur when dealing with congruency are:
- We may fail to note the exact value of a particular side or angle of the given triangle.
- We may use AAA, that is Angle-Angle-Angle, congruency to create congruent triangles.
- Proper instrumentation is needed for the measurement and estimation of congruency.
Want more help with your geometry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Congruency Homework Questions from Fellow Students
Browse our recently answered Congruency homework questions.