What is Eccentricity?
Before diving into the topic, first discuss eccentricity and then about the ellipse. Eccentricity of any conic section is used for determining the unique characterization of shape and one important thing is that eccentricity is a non-negative real number. The conic section can be a circle, ellipse, parabola or hyperbola. In a conic section, the eccentricity can be defined as the ratio of the distance to the foci and the line. It is one of the key parameters used by engineers in design. It tells about the shape and deviation from true shape.
Concept
The term eccentricity is defined from the fixed point and the fixed line in the plane. The fixed point is usually called as the focus and the fixed line is known as the directrix.
Eccentricity tells about how the deviation of the curve has occurred from the circularity of the given shape. Depending on the position of intersection of the plane with respect to the plane and the angle made by the vertical axis of the cone provide different types of conic sections. In the conic section, the parabola and hyperbola are open in shape and they both are unbounded.
If the eccentricity of any two conic sections is same then the two conic sections are similar and conversely. For any conic section, the value of eccentricity is constant. Now let’s see how the ellipse looks? The ellipse used to look oval in shape. An ellipse can be defined as a plane curve and the sum of their distance from two fixed points in the plane is a constant value such that the locus of all those points in a plane is an ellipse. And the fixed points in the ellipse are said to be the foci and it is also known as singular focus and it is surrounded by the curve. Since the ellipse is oval in shape, it is a closed curve.
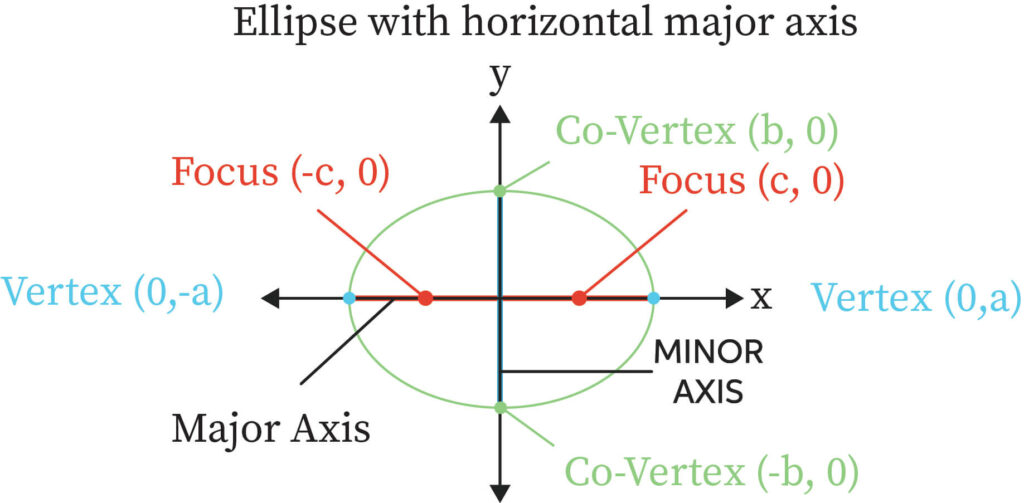
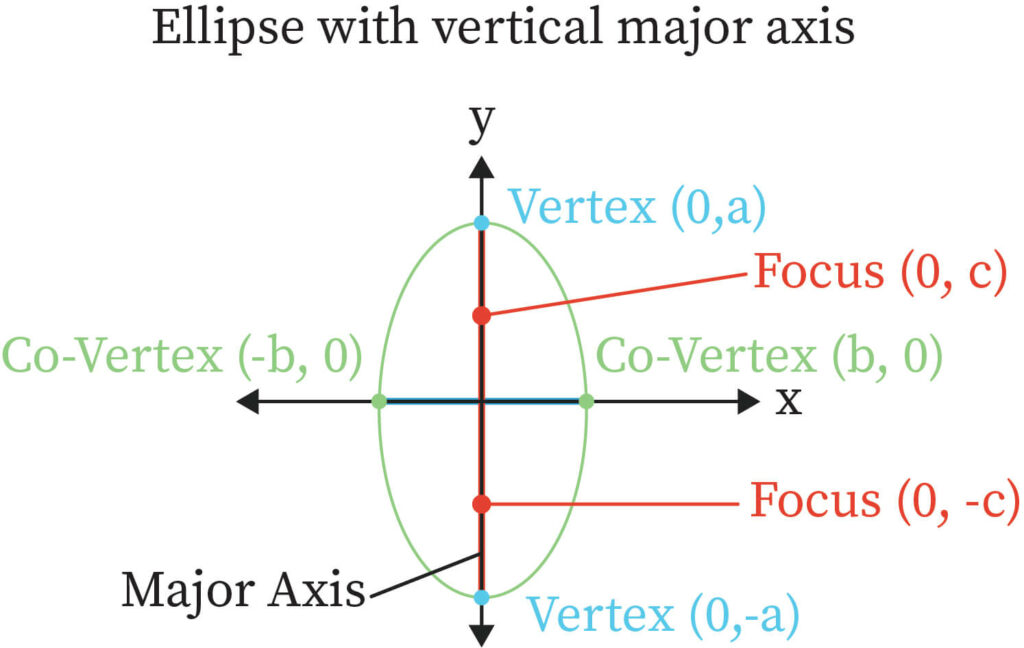
The major and the minor axes in the ellipse are one and it has a center in it. The half of the major and the minor axes are called the semi-major axis and semi-minor axis.
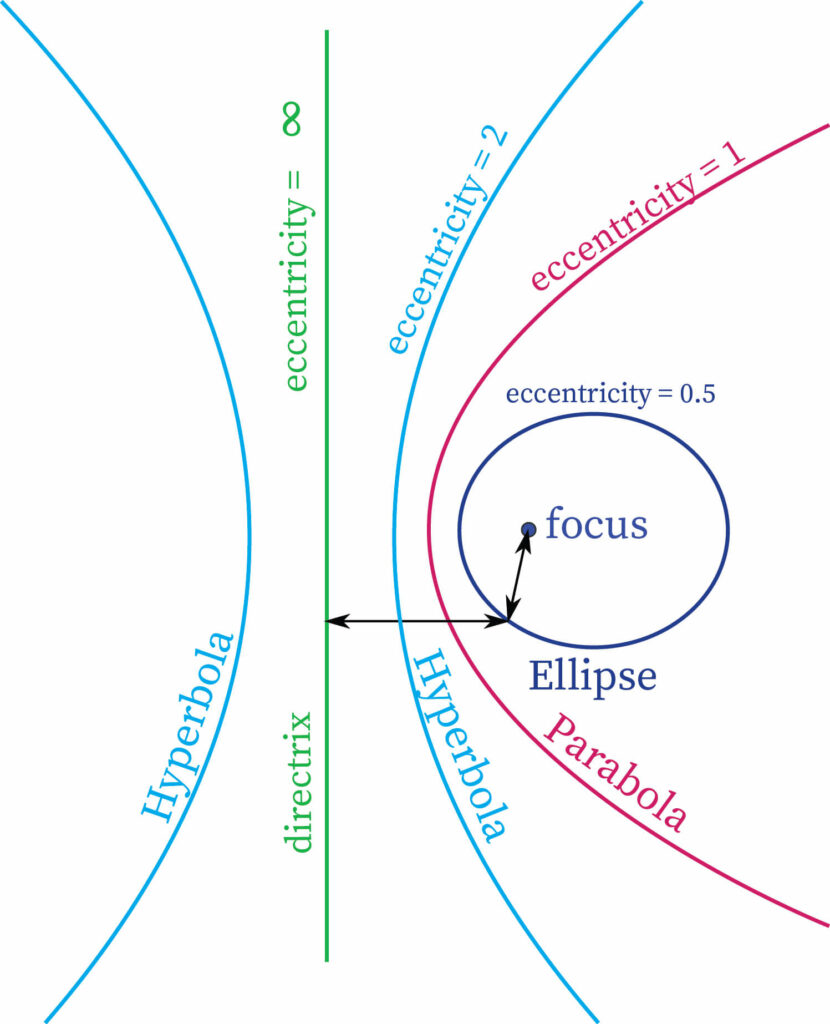
Values of Eccentricity
If the value of eccentricity is large then the curve is small. The eccentricity is usually denoted by e.
- If the eccentricity is 0 then the curve is a circle.
- If the eccentricity lies between 0 and 1 (that is 0<e<1) then the curve is an ellipse.
- If the eccentricity is 1 then the curve is a parabola.
- If the eccentricity is greater than 1 (that is ) then the curve is a hyperbola.
- If the eccentricity is infinite then the curve is a line.
Sometimes students may assume the eccentricity of a circle to the eccentricity of an ellipse, but it is totally different. Since the eccentricity of a circle is equal to zero and the eccentricity of an ellipse is strictly greater than zero and strictly less than one, so the eccentricity of an ellipse cannot be equal to zero. Later the discussion will start regarding some formulas for calculating the eccentricity of an ellipse and hyperbola and also for any conic section. Let us visualize how the curves of the above eccentricity are plotted in the plane. It is shown below in figure 1.
Ellipses can be found both in natural as well as in artificial objects. In today's life most of the objects are in elliptical shape like a rugby ball (because by rotating an ellipse about its major axis, the result will be a ruby ball). In the solar system, the path of each planet is elliptical with the sun at one of the foci. In lithotripsy, doctors use an elliptical tub for patients to lie on it to treat the kidney stone without surgery by passing the shock waves generated from one focus to the other foci that destroy the stone into sand like particles which can be easily passed through the body. This is how they treat kidney stones using the elliptical tub. In constructing buildings the roof is made elliptical because a person can hear far away sound from the other focal point. For instance, the roof of the Mormon Tabernacle in Salt Lake City is constructed in the shape of an ellipse when the ellipse is rotated about its major axis gives the auditorium an unusual acoustic property because of its reflective property (that is when a pin is dropped at one focus the person standing at the other focus can hear the sound clearly). The ellipse is widely used for esthetic purposes, in the design of formal gardens, in table tops, In mirrors, in picture frames, and in decorative purposes.
Formula
- Equation of a circle is where r is the radius of the circle.
- Equation of an ellipse is or where a is the length of the semi-major axis and b is the length of the semi-minor axis.
- Equation of a parabola is where a is the distance from the origin to the focus.
- Equation of a hyperbola is or where a is the length of the semi-major axis and b is the length of the semi-minor axis.
- Eccentricity for an ellipse is .
- Eccentricity for a hyperbola is .
- The general equation for any conic section in quadratic form is.
In general, the formula for eccentricity of any conic section can be written as, where c is the distance from centre to focus and a is the distance from center to vertex.
Practice Problem
Find the eccentricity of an ellipse for the equation .
Given:
To find:
Eccentricity of an ellipse.
The general form of an ellipse is .
First convert the given equation into the general form of an ellipse.
Divide the given equation by 400 that is.
From this and and
The formula of eccentricity for an ellipse is,
Therefore, the eccentricity of an ellipse for a given equation is 0.6.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelors of Science in Mathematics
- Masters of Science in Mathematics
Want more help with your geometry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Eccentricity of an Ellipse Homework Questions from Fellow Students
Browse our recently answered Eccentricity of an Ellipse homework questions.