What is an Isometric Transformation?

A shape-preserving transformation in the plane or space is an isometric transformation. As objects move in the coordinate plane, they transform in geometric terms. In other words, a transformation transforms a set of coordinate points into a different set of coordinates. A transformation alters a figure's scale, shape, or location and generates a new image. An isometry does not alter the size or shape of the figure. The size or shape of the figure is not altered by an isometry. A transformation in geometry is either rigid or non-rigid. Isometry is another term for a rigid transformation.

Thus, by definition, a transformation maps or transfers an initial image (preimage) to a final image (image). An object's size, location, or orientation may all change during transformation.

A transformation that retains the distance and angles between the original shape and the shape that has been transformed is an isometric transformation. Any image in a plane can be transformed using various operations.

Categories of Transformation

A transformation can be classified into one of two categories.

1. Rigid or Isomeric Transformation-

A transformation in which the preimage's scale remains constant is called a rigid transformation.

2. Non-Rigid or Non-Isomeric Transformation-

 A transformation in which the preimage's scale changes but not the shape is called a non-rigid transformation.

There are five different forms of transformations depending on how the image is modified. One of them is a non-rigid transformation, while the others are all rigid transformations. The five transformations are as follows:

• Translation
• Reflection
• Rotation
• Glide Reflection
• Enlargement

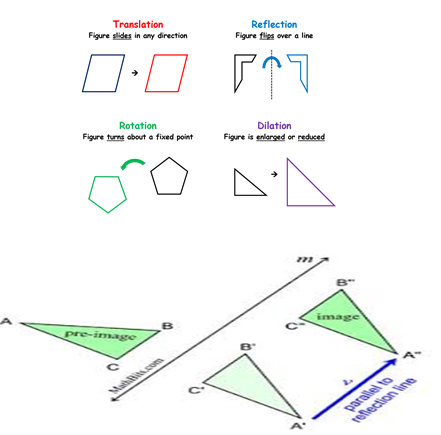
Translation (Slide)

You slide it around when you transform an object into a plane. An isometry is a translation in the plane that shifts a fixed distance in a fixed direction at each point in the plane. You're not going to flip, turn, twist, or bop it. Actually, for translations, you know where they all go if you know where one point goes. Translations retain orientation: left remains left, right remains right, top remains top, and the bottom remains bottom. Proper isometries are referred to as isometries that cover orientations. Sliding a figure is a translation.

A translation is described by stating the movement's path and the object's distance travelled.

For example, in the figure below triangle ABC is translated 5 units to the left and 3 units up to get the triangle A'B'C' image.

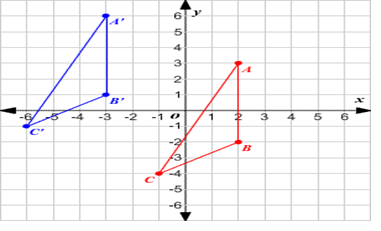
Formula to Calculate Translation

We can draw the translation in the coordinate plane if we know the direction and how far the figure should be moved. Using P'(x+a, y+b) to translate the point P (x, y), a unit right and b units up.

Reflection

Reflection is the second type of transformation. A reflection in the plane shifts an object into a new location that is the original position's mirror image. The mirror, called the axis of reflection, is a line. If you know the axis of reflection, everything there is to know about isometry is understood. The orientation changes in the reflection.

Reflections are tricky since the reference frame shifts. Depending on the axis of reflection, the left can become right, and the top can become lower. The image and object lie on opposite sides of the mirror line. The mirror line is perpendicular to the line connecting any object point to its corresponding image point. The mirror line divides the plane into two equal sections that overlap and is called an axis of bilateral symmetry.

They are called improper isometries since reflections alter the orientation. For example, the following figure shows the ABC triangle mirrored across the y=x+2 axis.

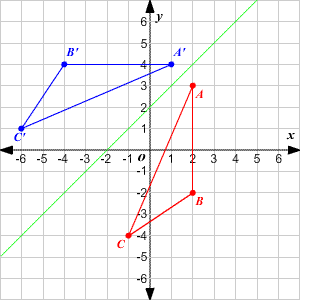
Formula to Calculate Reflection

The law for x-axis reflection is point P(x, y) becomes P’(x, -y).

Rotations

The rotation is a third type of transformation. A rotation is a geometric transformation that involves turning or rotating an object around a fixed point called the center of rotation.

The angle of rotation determines the size of the turn.

A rotation requires an isometry that holds one point fixed and changes a certain angle relative to the fixed point to all other points. You have to know the pivot point, called the center of the rotation, in order to define a rotation. You also have to know the amount of rotation.

An angle and a direction determine this. For example, you might rotate a figure at an angle of 90⁰ around point P, but you need to know whether the rotation is clockwise or counterclockwise. Some examples of rotations concerning some points are shown in the figure below.

Other than the rotation of the identity, rotations have one fixed point: the rotation center. You don't change it if you turn a point around, so it doesn't have any scale. A rotation retains orientation, as well. All rotate in the same direction at the same angle, so left remains left, and right remains right. The figure below shows a 90 ° clockwise rotation of the triangle ABC around the origin.

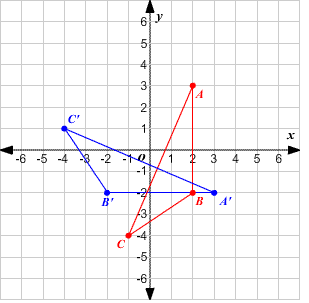
Formula to Calculate Rotation

Phase 1: In the specified figure, pick any point and link the chosen point to the rotation center.

Phase 2: Locate and attach the image of the chosen point to the center of the rotation. Phase 3: Calculate the angle of the two lines between them. The angle sign is dependent on the direction of rotation.

Glide Reflections

A glide reflection is a symmetry operation in 2-dimensional geometry that combines reflection over a line and translation along that line into a single operation. Note that there has been a shift in orientation. The two-component transformations can be performed in any order in a glide reflection. The footprints are glide reflections of each other. The initial "move" on the left foot is seen on the left, followed by the "step" on the right foot, which is the "result" of the glide reflection on the left. Glide reflections are improper isometries because the orientation has shifted.

The translation and the axis of reflection are parallel. When you know how two points are moved, it is simple to decide the axis of reflection.

Enlargement

Dilation, also known as enlargement, is a transformation in which the size of an object changes but not its shape. The scale factor of the enlargement determines the size change. Enlargement is also known as a scale transformation.

When explaining an enlargement (or dilation), we must always provide the following information:

1. The location of the enlargement's base, which indicates where the enlargement is measured.

2. The enlargement's scale factor, which indicates how much the object has been expanded or reduced to create the picture.

Enlargement and reduction are the two main forms of dilations. The image is larger than the object (enlargement) when the scale factor (k ) is greater than one, and the image is smaller than the object when the scale factor ( k) is less than one (reduction).

The scale factor of dilation may be positive or negative. The object and image are on the same side of the center when the scale factor is positive. The object and image are on opposite sides of the center when the scale factor is negative.

Common Mistakes

The students may face some deficiencies in determining the symmetry axis of geometric shapes.

The most common mistakes revealed that the students understood the algebraic meaning of translation and rotation but not the geometric meaning.

Context & Applications

The topic is relevant in the following areas:

• High school Level
• Graduation Level
• Engineering
• Architecture

Related Concepts

• Reflection
• Translation
• Rotation
• Dilation