What is a Limacon?

The route of a point attached to a circle when that circle rolls around the perimeter of another circle of equal radius is defined as a limacon. It is commonly known as a limaçon of Pascal. It's also known as the roulette wheel, which is produced when it rotates around a circle with half its radius, resulting in the smaller circle being within the bigger circle.

The polar curve is commonly used to describe limacon. When a circle is allowed to rotate around another circle, the fixed point of the circle forms a path. It is the name given to this route. The radii of both circles do not have to be the same.

History of Limacon

The limacon of Pascal was discovered by Etienne Pascal (who is the father of scientist Mr. Blaise Pascal). The curve was named by a French person Gilles-de Roberval in the year 1650 when he first used it as an example for his methods of drawing tangents, which is now read as differentiation.

The name ‘limacon comes from the Latin word ‘limax’ which means ‘a snail’.

The German scientist Albrecht Durer should also be given the credit for discovering this one since he has a method to draw a limacon, but he didn’t call it limacon at that time.

Equations of Limacon

The Limacon curves resemble circles. They come in a variety of shapes and sizes, based on the values in their equations.

A limacon in the polar coordinates is written in the form $r=b+a\cos \theta$.

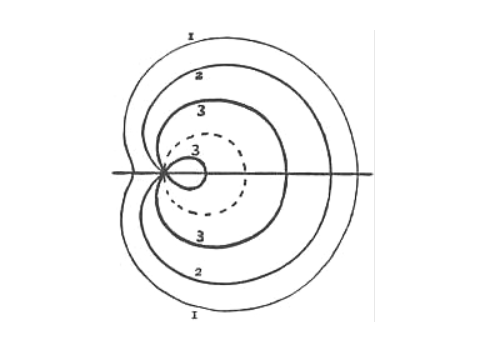
When b = 2a then this limacon becomes a cardioid but if b = a, it becomes a trisectrix. Note down it is not the trisectrix of Maclaurin. Below is the diagram of a limacon for different values of a and b.

The polar equation can be changed to new coordinates by multiplying r to both sides of the equation (now including the point at origin) and using $r^2=x^2+y^2$ and $r\cos \theta =x$ to obtain:

$\begin{array}{l}r=b+a\cos \theta \\ r^2=br+ar\cos \theta \\ x^2+y^2=b\sqrt{x^2+y^2}+ax\\ x^2+y^2-ax=b\sqrt{x^2+y^2}\\ {\left(x^2+y^2-ax\right)}^2=b^{{}^2}\left(x^2+y^2\right)\end{array}$.

Now using the parametric structure of the polar to Cartesian change, we obtain:

Limacon and Related Terms

Using the substitution $z=x+iy=\left(b+a\cos \theta \right)\left(\cos \theta +i\sin \theta \right)$, the parameterization in the complex coordinates is obtained as:

Now if we shift horizontally by -a/2, the new coordinates become:

This can be done by changing the location of the origin. This would result in converting the equation to the equation of a centered trochoid.

Note that this change in the independent variable denotes that the default polar coordinate parameterization $\theta =\arg z$ is no longer being used.

Special Cases

1. If a=b, the polar equation becomes:

$r=b\left(1+\cos \theta \right)=2b{\cos }^2\frac{\theta }{2}$

Or

$r^{\frac{1}{2}}={\left(2b\right)}^{\frac{1}{2}}\cos \frac{\theta }{2}$

So the curve becomes a member of the family of sinusoidal curves, and this special type is termed cardioid.

2. If a=2b, then the polar equation becomes:

$r=2b\cos \frac{\theta }{3}$

So the curve becomes a member of the family of rose curves, and this special type is termed trisectrix, or limacon trisectrix.

In this case, the centroid trochoid equation becomes,$\begin{array}{l}z=b\left(e^{it}+e^{2it}\right)=b{e}^{\frac{3it}{2}}(e^{\frac{it}{2}}+e^{\frac{-it}{2}})=2b{e}^{\frac{3it}{2}}\cos \frac{t}{2}\\ \end{array}$

Types of Limacon Curve

• Looped
• Polar 
• Cardioid
• Dimpled

In the instance of limacon, there are a few cases that need to be addressed. These scenarios are based on a and b's connection. There are five instances in all, each demonstrating a different form. These are the following:

Case I: If b is bigger than a, the limacon that results is a simple closed curve.

Case II: If the value of b falls between a and 2a, the limacon pattern will be dimpled.

Case III: If the value of a equals the value of b, the limacon generated is a cardioid.

Case IV: If the value of b is smaller than the value of a, limacon will include an inner loop.

Case V: If b is equal to half of a, the limacon will have a trisectrix pattern.

Relation Between other Loops and this one

Consider that there is a point P and a circle C such that the center of the circle is not at P. The collection of those circles that pass through P such that their centers lie on C is a limacon.

An orthogonal projection of the circle now is called a limacon. The projection with respect to the origin of the circle with radius b, centered at (a, 0) has the equation $r=b+a\cos \theta$.

The opposite concerning the circle of $r=b+a\cos \theta$ is $r=\frac{1}{b+a\cos \theta }$. The inverse obtained is a conic with the focus at origin and eccentricity $\frac{a}{b}$.

In this way, any limacon can be defined as the inverse of a conic such that the foci is the center of inversion. The inverse of the parabola will become a cardioid in this case. The inverse of a hyperbola will become the limacon with an inner loop. The inverse of an ellipse will become a limacon with no loop.

Now the conchoid of this circle, with respect to a place here on the circle, is a limacon.

One special limacon is the Cartesian oval.

Common Mistakes

In this people are most likely to get confused between the different types of curves that are there in this and the formula which is a lot to understand.

Context and Applications

• Limacon has a wide range of applications in mechanical and machine design engineering.
• They are utilized to create a variety of machines, including gear machines, screw machines, and vane machines.
• Their patterns are frequently utilized in the design of control systems.
• This topic is significant in the professional exams for both undergraduate and graduate courses, especially for B.Sc. and M.Sc.

Related Topics

• Bean
• Cardioid
• Evolute