What are Lines and Angles?
In a two-dimensional plane, a line is simply a figure that joins two points. Usually, lines are used for presenting objects that are straight in shape and have minimal depth or width.
An angle is something that forms when two lines intersect at some point. The term vertex is used for marking this point of intersection of the straight lines.
The concept of line in mathematics is very old. Since ancient times, mathematics has seen the use of lines for the representation of objects. Famous Greek mathematician Euclid called line a shape of breadth-less length. Euclidean geometry is entirely based on the concept of lines.
What is a Line?
By definition, a line is a path that connects more than one point. It can have an infinite length, and there are no endpoints in a line. A line segment is a line’s part. When any line has a segment, or when it has two endpoints, it is said to be a line segment.
A single plane can have multiple line segments or lines in it. Lines and angles consist of the founding base of geometry. The basic types, definitions, and properties of lines and angles have been discussed in the article below.
What are the Different Types of Lines?
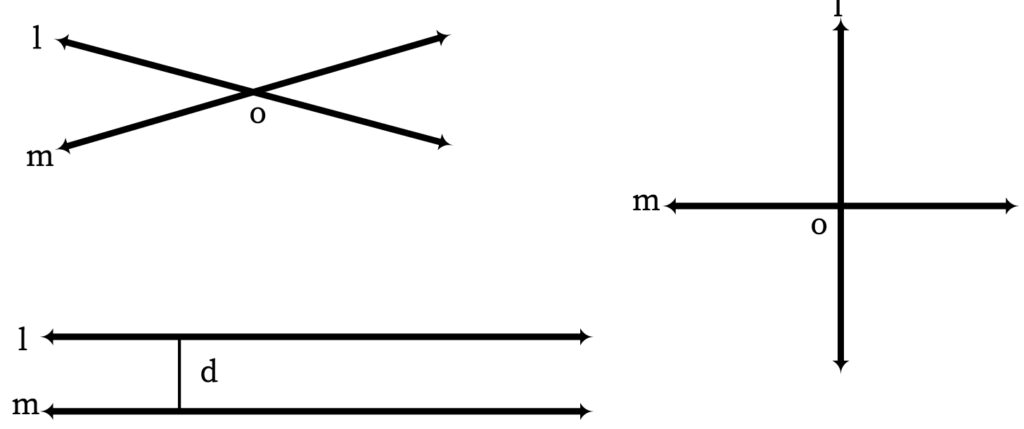
Lines can be categorized into multiple types on the basis of the position and distance that one line has from another line. The major types of lines are given below:
- Intersecting Lines: If two or more lines meet each other at a single point, then the lines are said to be intersecting lines.
- Parallel Lines: These are lines that have the same amount of distance between them in all instances. In other words, these lines will never intersect with each other. Two or more lines can be parallel to each other.
- Transversal Line: A line that can cut or pass through multiple lines at different points is known as a transversal line. These are intersecting lines when more than one line is intersected by the same line. That way, two or more lines are intersected by the transversal line at different points.
What is an Angle?
If two straight lines meet in the same plane, then their inclination towards each other at the point of intersection is the angle between them. The measurement of the angle is done along the intersecting vertex. We use the symbol “∠” for representing an angle. In an angle, there is one single common vertex, which is the point of intersection of the lines. There are two legs of an angle. These are the spread lines that have been divided by the vertex.
It is important to note that the order of the leg points can be chosen as per our wish. When the angle is named, usually three vertices are used in the notation. As long as the middle letter denotes the vertex, the position of the other leg points is not important. For example, if we write ∠AOB, it means that O is the common vertex. In this manner, ∠BOA has the same value as ∠AOB. Usually, degrees are used to measure angles. An angle can have 0 degrees to a maximum of 360 degrees in total.
How Many Types of Angles Are There?
Angles are mainly classified on the basis of their measurement. In this respect, there are four different types of angles. They are:
- Acute Angle: In an acute angle, the measurement of the angle is between 0 and 90 degrees. Any angle that has a value less than 90 degrees is an acute angle.
- Right Angle: The angle measurement will be precisely 90 degrees in case of a right angle. When two lines create such an angle, then these lines are perpendicular lines. In other words, two lines can only be perpendicular to each other if they form 90 degrees between them.
- Obtuse Angle: The measurement of some angles can go from 90 degrees to 180 degrees. These angles are known as obtuse angles. Such an angle is greater than any right angle and any acute angle. If any right angle and any acute angle are added, then we get an obtuse angle.
- Straight Angle: The angle measurement will be precisely 180 degrees in case of a straight angle. We usually measure an angle from the point of intersection between two lines. However, an angle can be measured from any point in a line. If we consider any point in a straight line and measure the angle, we will have 180 degrees. Therefore, any straight line has 180 degrees as its measurement.
- Reflex Angle: When an angle has a value of greater than 180 degrees, but smaller than 360 degrees, then this angle is known as a reflex angle.
- Complete Angle: When a point situated in a straight line is measured along with all four coordinates, then the measured angle is 360 degrees in total. This is because a straight line measures 180 degrees on each side. An angle measuring 360 degrees is called a complete angle.
What Other Types of Angles Are There?
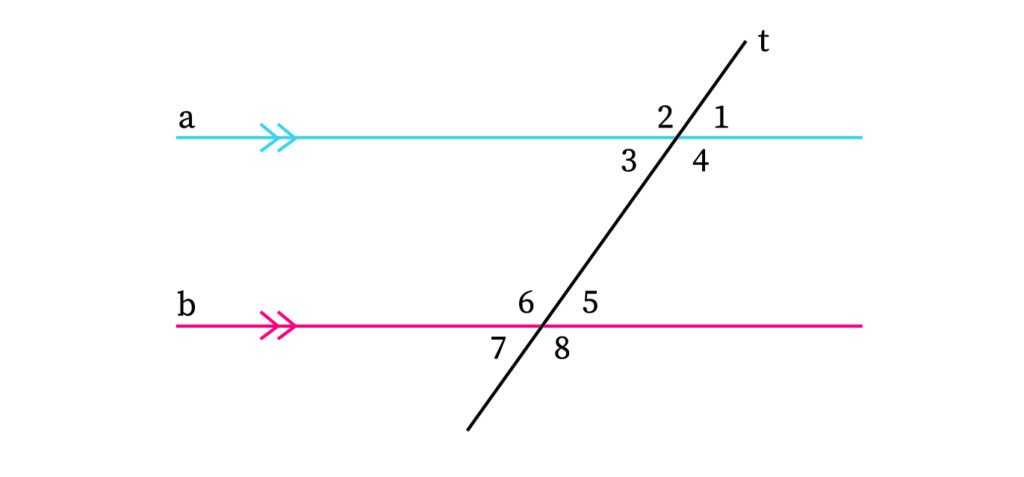
Until now, we have discussed angles based on their measurements. However, angles can also be classified depending on how they relate with each other. Angles can be formed by the intersection of two lines or formed when a transversal cuts between them.
The different types of angles based on their correlation with each other are given below.
- Vertically Opposite Angles: There are a total of four angles formed when only two lines intersect. Among these four points, two angles are formed exactly opposite to each other along with the intersecting point. These angles are vertically opposite to each other. The value of these angles is also the same. From the above diagram, (1, 3), (2, 4), (6, 8), and (5, 7) are vertically opposite angles.
- Interior and Exterior Angles: If a transversal line cuts through two straight lines, then a total of eight angles are created. The region between the two lines is treated differently than the region outside the two lines. The angles that are present inside this region are known as interior angles, and the angles located outside this region are known as exterior angles.
- Corresponding Angles: Corresponding angles are the set of angles that lie on the same side of the area formed by the transversal lines. In such cases, the set of corresponding angles are an interior angle and an exterior angle.
- Alternate Interior Angles: A transversal line creates four interior angles. Among them, the alternate interior angles are the two angles that are placed on the different lines and on the opposite sides of the transversal.
- Alternate Exterior Angles: Similarly, alternate exterior angles are the set of exterior angles that are located on the opposite sides of the transversal line.
These are the types of angles that are correlated with each other. In special cases, a transversal line can cut through two lines that are parallel to each other. In such a case, the corresponding, alternate interior, and alternate exterior angles are all equal in value.
Practice Problem
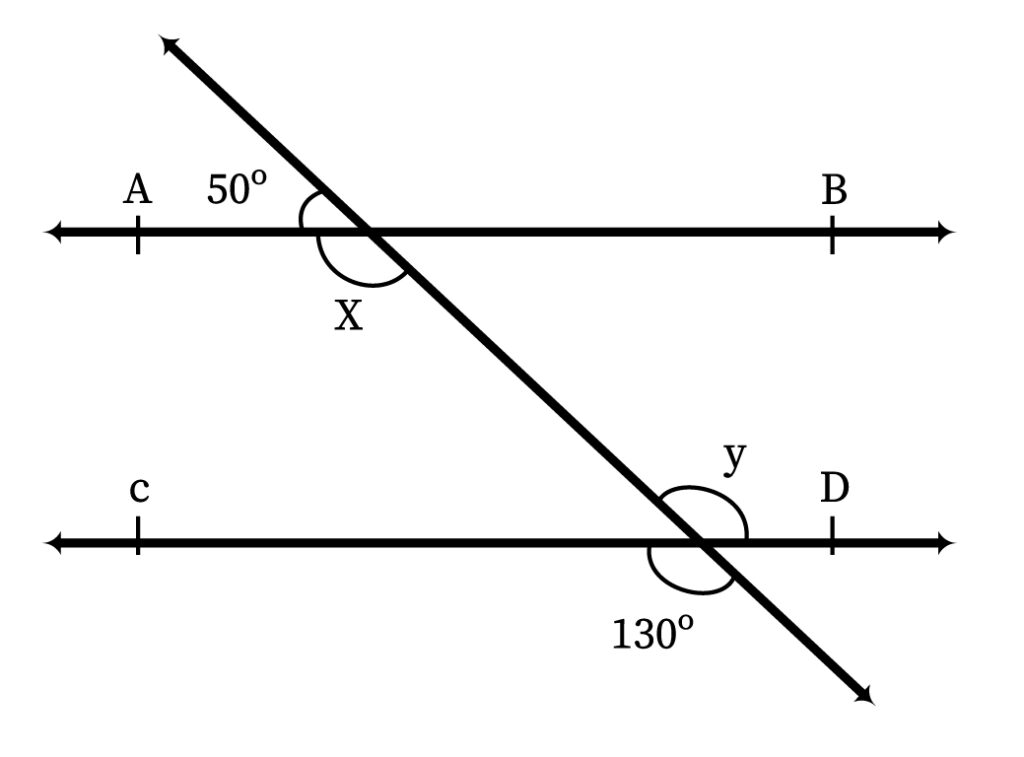
In the given diagram, find x and y.
In the diagram, x and the 50 degrees angle lie on the same straight line.
Therefore, x = 180-50 degrees = 130 degrees.
Also, y is a vertically opposite angle to 130 degrees. Hence, y = 130 degrees.
We can also see that x and y are alternate angles. Hence, x = y = 130 degrees.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- B.S. in Mathematics
- M.S. in Mathematics
Want more help with your geometry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Lines and Angles Homework Questions from Fellow Students
Browse our recently answered Lines and Angles homework questions.