What is Maximization?
Have you ever seen a bridge in the shape of a parabola? Where is its maximum on the bridge? The maximum of that bridge is the highest point on that bridge. The process of finding the maximum of the bridge here is called the maximization.
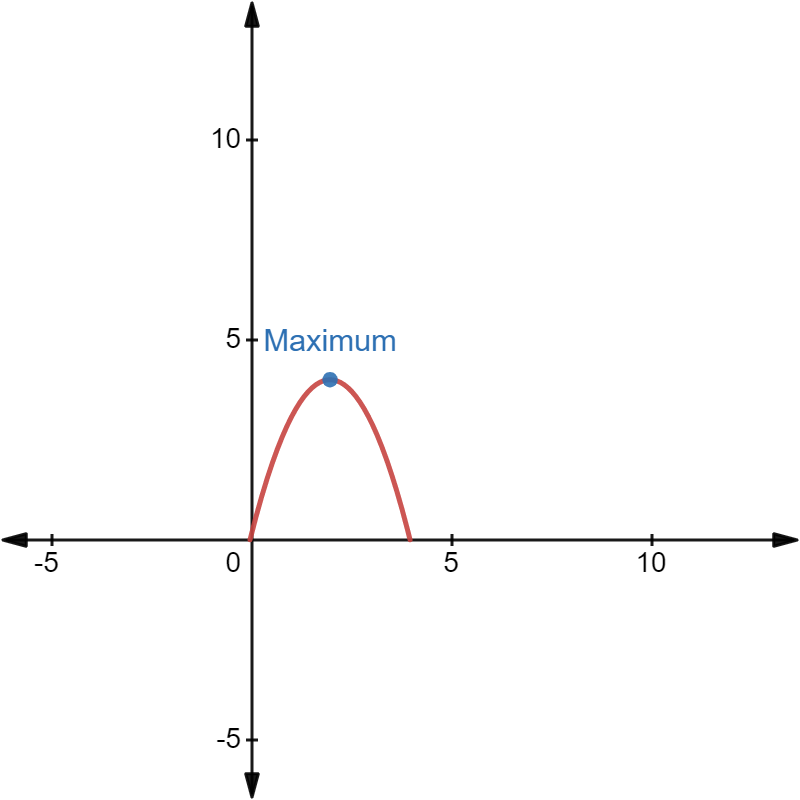
Have you thrown a ball from a point to another such that it makes the path of a parabola over a given time? Where is the velocity of the ball zero? The highest point of the path gives the velocity zero at a given time.
Mathematical Formula for Maximization
Suppose a curve is given in the form of a function f(x) on an interval I and let c be any point belonging to the interval. Then, the curve f(x) is maximum at the point c for all x in the interval, if we have the condition:
f(x)≤f(c) for all x∈I
Insight into First Derivative and Second Derivative Test
- Let a function g be continuous on a closed interval [c,d] and twice differentiable on the open interval (c,d).
- If the first derivative of the function is greater than zero that is g’(x) > 0 for every x in, (c,d) then the function g is increasing on interval [c,d].
- If the first derivative of the function is less than zero that is g’(x) < 0 for every x in (c,d), then the function g is decreasing on interval [c,d].
- When the second derivative is greater than zero the curve is concave up and when the second derivative is less than zero the curve is concave down.
If a is a critical number for the function g, then local extrema are as follows,
- If the first derivative of the function, that is g’, changes its sign from positive to negative at a, then g(a) is called the local maximum of g.
- If the first derivative of the function, that is g’, changes its sign from negative to positive at a, then g(a) is called the local minimum of g.
- When the second derivative is greater than zero at a, then g(a) is the local minimum of g, and when the second derivative is less than zero at a, then g(a) is the local maximum of g.
Types of Maximum
This is of two types: one is absolute or global and the other one is a relative maximum.
Absolute or Global Maximum
The maximum of the curve f(x) at point c in the interval I is called the absolute or global maximum. Here, the absolute or global maximum is used for the maximum in the given interval. The absolute or global maximum of the curve can occur at the endpoints or the interior points of the interval.
Calculate where is the maximum profit when the revenue function is R(x)=−0.01x2+45x and the cost function is C(x)=15x+1450 in the interval [−2,3]?
The profit function can be obtained using the formula:
Profit =Revenue - Cost
So, the profit function is:
P(x)=R(x)−C(x)
=(−0.01x2+45x)−(15x+1450)
=−0.01x2+30x−1450
Plot the graph of the profit function on the interval [30,2970].
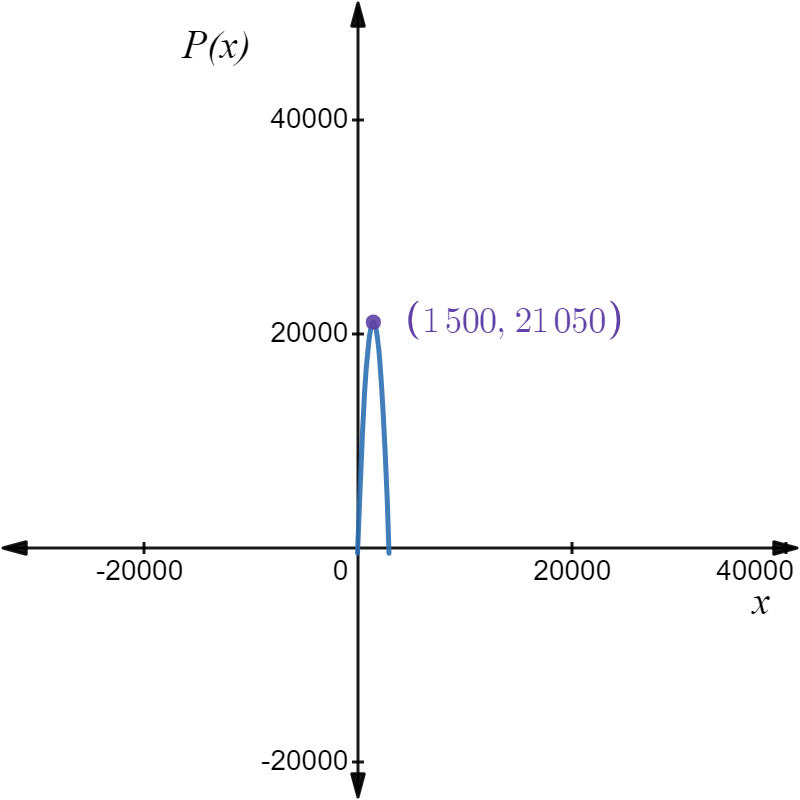
The maximum profit of the profit function is at the point (1500,21050) which is the absolute or global maximum in the interval [30,2970] at point x=1500. This occurs in the interior (inside) of the interval.
Relative Maximum
The term relative is used for those points which are nearer to point c. Let there be points nearer to c which forms an open interval around c. Then the curve f(x) has a relative maximum at point c if f(c) is greater or equal than f(x) for all the points lying in the open interval.
Note
- Relative maximum always occurs at interior points.
- Check the relative maximum in the given figure on the interval [-2,2].

- In this case, suppose we don’t know the function but have an idea of the interval and know where the relative maximum occurs.
- In the given figure, as x increases from left to right (or we move from left to right on the number line), the function also increases till x=0. After that, the x decreases till the next bend, and then again, the x increases. So, the relative maximum occurs at interior point x=0 as we move from left to right when x increases.
- Hence, the relative maximum occurs at point 0 as it has the maximum (when x increases) of the function in the open interval of points nearer to 0.
Points of Maximum: Critical Points
Suppose a curve is defined by f(x). If the derivative of the curve at point c is either zero, which means the tangent to the curve is parallel to the x-axis, or the derivative of the curve does not exist, then point c is called the critical point.
When Derivative Exists
Maximize the revenue for the demand function given by p(x)=−x+2 on interval [-2,4].
First, find the revenue function to maximize the revenue.
- The formula for revenue is R(x)=xp(x).
- So, R(x)=x(−x+2)=−x2+2x.
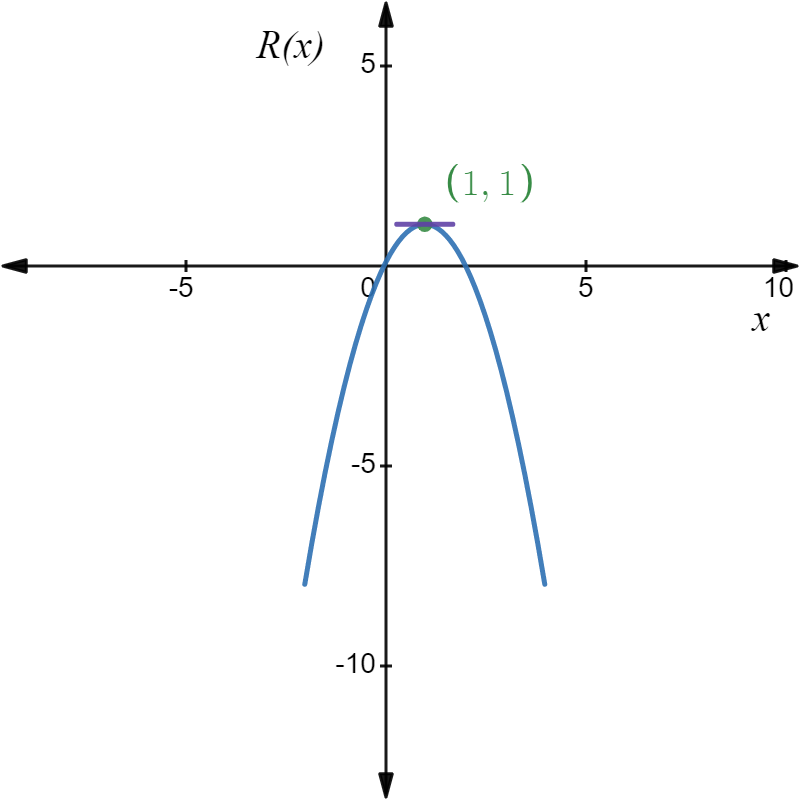
Differentiate the revenue function
R'(x)=−2x+2
- To maximize it, first check where the derivative is zero. So, it is zero for x=1.
- On substituting x=1, the maximized revenue is 1.
- Also, the tangent at point (1,1) is parallel to the x-axis as shown in figure 4.
When Derivative Does Not Exist
Maximize the curve f(x)=−|x| on the interval [-2,2].
Answer:
- Differentiate the curve f(x)=−|x| to maximize it.
- The derivative of the curve f(x)=−|x| does not exist at point 0 as the left-hand derivative is 1 and the right-hand derivative is -1. (Using the definition of differentiability by the first principle.)
- Geometrically, the curve is sharp at point (0,0), so tangent does not exist. So, at the critical number (0,0), we will maximize the curve.
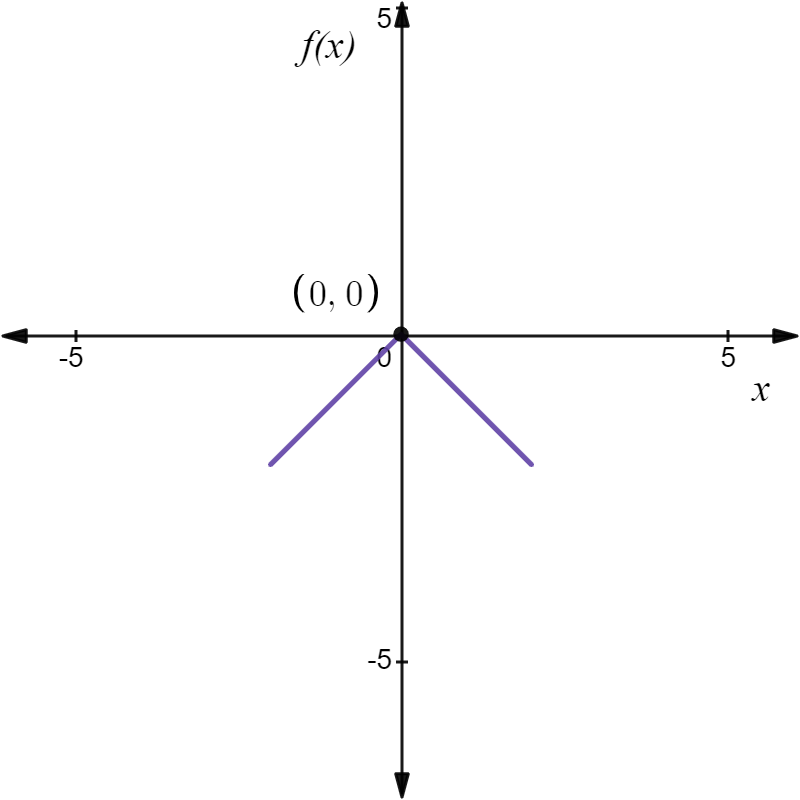
Use of Critical Points
Relative maximum occurs at critical points only. So, the derivative of the curve at that point is either zero or does not exist.
Maximization of a Curve
Suppose a curve f(x) is continuous on a closed interval, which means the curve does not break at any point in the interval, then using the following steps, maximization of a curve can be obtained:
1) Calculate the Critical Points of the Curve
- Calculate the derivative of the given curve.
- Equate the derivative of the given curve to zero.
- Calculate the x for which the derivative is zero or the derivative does not exist.
2) Calculate the Curve at Critical Points
Substitute each critical point x obtained from step 1 in the curve f(x).
3) Calculate the Curve at End Points
Substitute both endpoints in the curve f(x).
4) Find the Maximum
Check for all the points obtained in step 2 and step 3 to identify which of them has the maximum. The maximum of the curve is the desired result.
The process of finding the maximum of the curve f(x) from step 1 to step 4 is called maximization.
Examples
1. Find the maximum for the curve f(x)=2x3−3x2 in the interval [-1,2].
Answer:
First, check whether the function is continuous or not in the closed interval [-1,2]. The curve is a polynomial function and every polynomial function is continuous on a closed interval.
Hence, the curve f(x)=2x3−3x2 is continuous on the interval [-1,2].
Step 1) Calculate the derivative of the given curve f(x)=2x3−3x2.
The derivative of the curve f(x)=2x3−3x2 is:
ddx(f(x))=ddx(2x3−3x2)
f'(x)=6x2−6x
Step 2) Equate the derivative of the given curve f(x)=2x3−3x2 to zero.
f'(x)=0
6x2−6x=0
Step 3) Calculate the x for which the derivative is zero or the derivative does not exist.
Solve the equation 6x2−6x=0 and find x.
6x2−6x=06(x2−1)=0x=0 or x=1
Thus, there are two critical points x=0 and x=1.
Step 4) Substitute each critical point x in the curve f(x).
- For x=0:
f(0)=2(0)3−3(0)2=0
- For x=1:
Step 5) Substitute the endpoints x in the curve f(x).
The endpoints of the interval [-1,2] are -1 and 2. So, calculate the curve at these points.
- For x=-1:
- For x=2:
- The maximum value of the curve is 4, which is obtained at x=2. Hence, (2,4) is the maximum value of the curve f(x)=2x3−3x2.
Verification
- The maximum value of the curve f(x)=2x3−3x2 can also be obtained using the graph of the curve.
- Plot the graph of the curve f(x)=2x3−3x2 in the interval [-1,2].
- The graph of the curve is as follows:
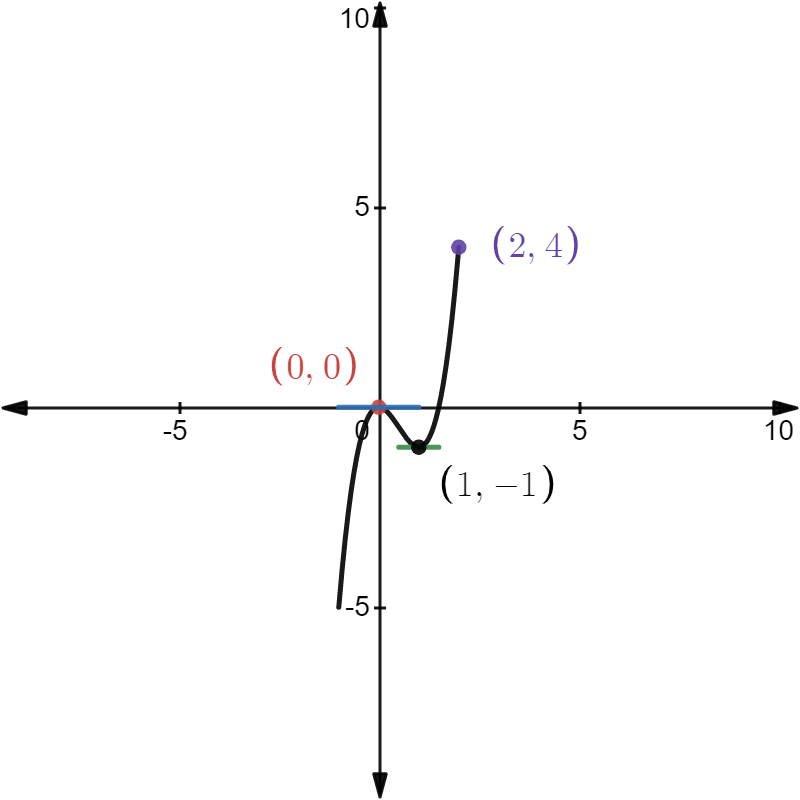
- From the above figure, the critical points occur at 0 and 1 as the tangents at these points are parallel to the x-axis. At point (0,0), the value of the curve is the relative maximum.
- At point (2,4), the value of the curve is maximum which is the absolute maximum or the global maximum of the curve.
- Similarly, the maximum of a curve can be obtained where the derivative does not exist.
1. Find the profit maximization for p(x)=24x−0.5x32−600 in the interval [0,2450].
- First, differentiate the function p(x)=24x−0.5x32−600 to find the profit maximization.
- Now equate the derivative to zero and find the critical points in order to find profit maximization.
p'(x)=0
24−0.75x12=0
x12=240.75
x12=32
x=1024
- There is only one critical find so calculate the function p(x)=24x−0.5x32−600 at critical point and at the endpoints.
For x=1024:
p(1024)=24(1024)−0.5(1024)32−600=7592- For x=0:
- For x=2450:
- Thus, the profit maximization occurs at x=1024 and it is 7592.
Verification
Plot the graph of the function p(x)=24x−0.5x32−600 in interval [0,2450].
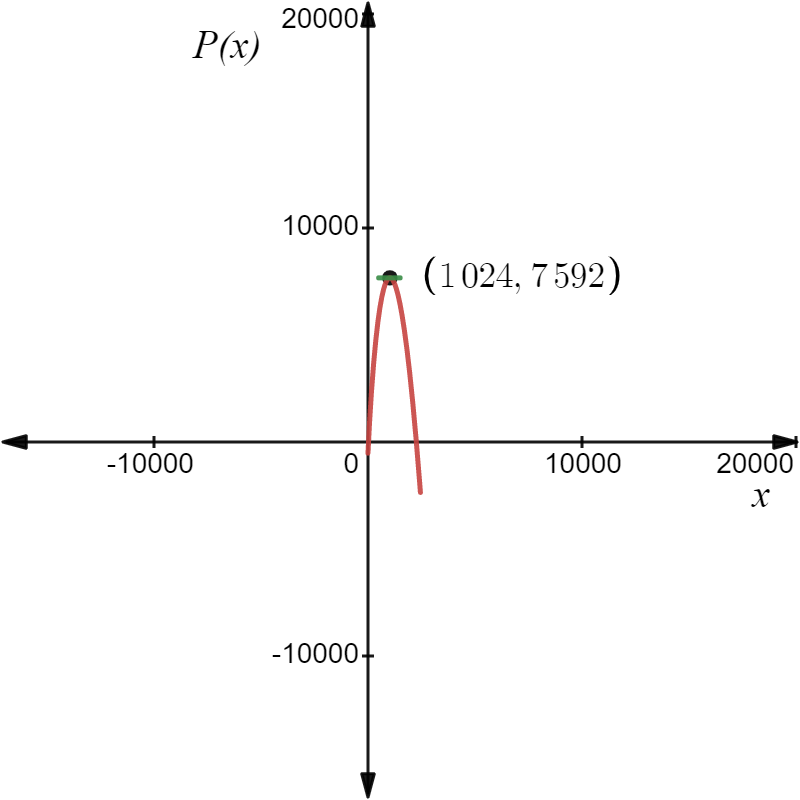
- The tangent is parallel to the x-axis or the derivative is zero at x=1024.
- Thus, from the figure the profit maximization occurs at x=1024.
Formula
The steps to find the maximum value of the function are:
- The function should be continuous and differentiate on the provided interval.
- We differentiate the function and equate the derivative to zero.
- Calculate the x for which the derivative is zero or the derivative does not exist.
- Substitute each critical point x in the curve f(x).
- Substitute the endpoints x in the curve f(x).
- Then observe the global and relative maximum.
Common Mistakes
Whenever the derivative of a function is calculated, if the derivative is in fraction form, then don’t multiply the denominator with zero instead find where the denominator is zero to find the critical points.
Context and Applications
This topic is significant in the professional exams for undergraduate and postgraduate courses, especially for
- B.Sc. in Science
- Bachelor of Arts
- Bachelor of Mathematics
Practice Problem
Calculate the maximum value of the curve f(x)=x−6x23 in the interval [-1,3].
Hint
Check separately where the denominator of the derivative and the numerator is zero. These are the critical points.
Answer:
First, check whether the function f(x)=x−6x23 is continuous in the closed interval [−1,3].
The function f(x)=x−6x23 is a polynomial function and every polynomial function is continuous on a closed interval. Hence, the curve f(x)=x−6x23 is continuous on the interval [−1,3].
Step 1) Calculate the derivative of the given curve f(x)=x−6x23.
The difference rule for differentiation states that ddx[f(x)−g(x)]=f′(x)−g′(x), where f(x) and g(x) are differentiable functions of x.
The power rule for differentiation states that ddx(xn)=nxn−1 , where n is a real number.
Differentiate on both sides of f(x)=x−6x23 with respect to x by the use of the difference and power rule of differentiation to obtain the first derivative of the function.
f'(x)=ddx(x−6x23)
=ddx(x)−6ddx(x23)
=1−6⋅23x−13
=1−4x13
Step 2) Equate the derivative of the given curve f(x)=x−6x23 to zero.
The critical point of a function f is a point in the domain of the function where the function is either not differentiable or the derivative is equal to zero.
Substitute f'(x)=0 in f'(x)=1−4x13 and then solve for x to obtain the zeros of the function.
1−4x13=0
4x13=1
4=x13
(4)3=(x13)3
64=x
x=64
Hence, x=64 is one of the critical points of f.
The function f'(x)=1−4x13 is not defined for x=0. Therefore, x=0 is the critical point of f.
Step 3) Calculate the value of f(x)=x−6x23 for each critical point in the curve f(x).
Calculate the value of the f(x)=x−6x23 at x=0.
f(0)=0−6(0)23
=0
Calculate the value of the f(x)=x−6x23 at x=64.
f(64)=64−6(64)23
=−32
Step 4) Calculate the value of the f(x)=x−6x23 at each end point.
Calculate the value of the f(x)=x−6x23 at x=−1.
f(−1)=(−1)−6(−1)23
=−7
Calculate the value of the f(x)=x−6x23 at x=3.
f(3)=(3)−6(3)23
≈−9.48
The maximum value of the curve is 0, which is obtained at x=0. Hence, (0,0) is the maximum value of the curve f(x)=x−6x23.
Verification
Plot the graph of the function f(x)=x−6x23. in interval[−1,3].
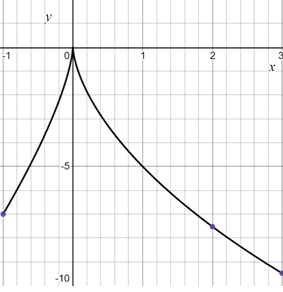
The figure shows that the profit maximization occurs at x=0. This verifies that the solution obtained is correct.
Want more help with your geometry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Maximization Homework Questions from Fellow Students
Browse our recently answered Maximization homework questions.