What is Mensuration?  

It is the branch of study in mathematics that involves measuring different parameters. It helps in measuring our surrounding objects. Ever since old days, people have always tried to measure and record different two-dimensional or 2D structures. However, the world is of three-dimensions, or 3D in short.

The idea of measurement   

World renowned Greek Mathematician of the ancient times Archimedes first came up with this idea. He had significant contributions in algebraic, arithmetic, geometric and mensuration calculations. He introduced mensuration mainly for the measuring of the area of different types of plane figures. Similarly, curved surfaces and their volumes were found out too.          

Units of measurement       

Previously, people mainly used different types of non-standard units for measuring different objects. These non-standard measuring units were mainly trivial, and they were not accurate in providing the size of the required object. Even today, many people use such methods to gain a rough estimate about the length, width, or height of any object. The most commonly used non-standard unit of measurement is hand spans. Similarly, foot spans are also used to roughly understand how big a room is.          

However, these are not very accurate for obvious reasons. Hence, standard methods of measurement were found out, which uses the different parameters like capacity, weight, or length. Nowadays, the standard units of measurements include meter, gram, liter, kilometer, or kilogram, and so on. These standard units of measurement can help in accurately finding out the mensuration and dimensions of any object.

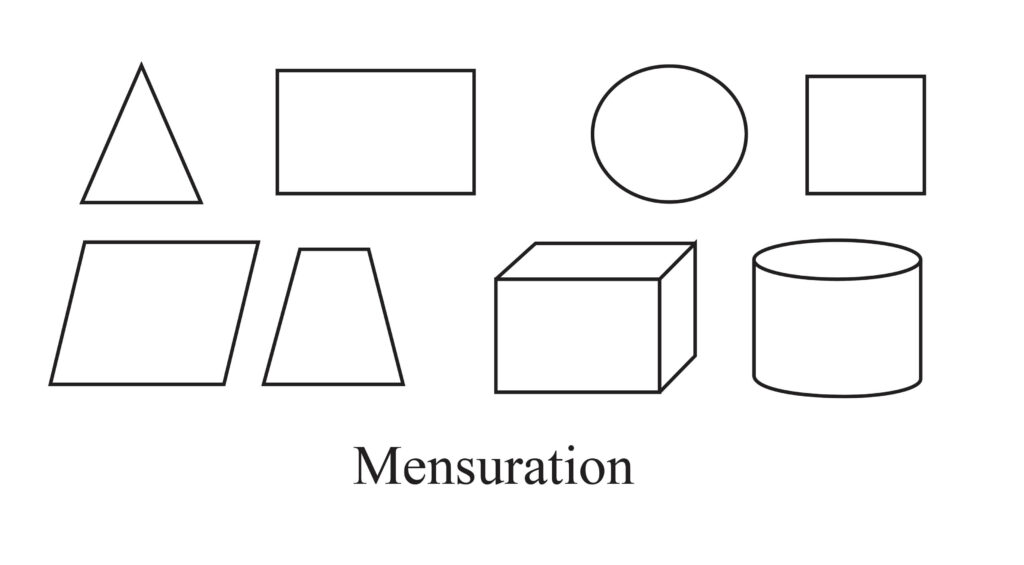
Two-dimensional shapes

Shapes like rectangle, square and circle do not have height or depth. They are called two-dimensional shapes and are mainly used for determining the perimeter or area.

Three-dimentional shapes      

Shapes like cone, cylinder, cube, and sphere have height and depth. They are called three-dimensional shapes and are used for determining the volume, depth or surface area.

What are the Important Terms in Mensuration?    

Some of the important terms in mensuration are given below with the SI units. The International System of Units, abbreviated as SI unit, is the standard system of measurement used all over the world.

Area – It is the total surface that is being occupied by a region closed or defined on all sides. Its SI unit is square meter.

Perimeter – It is the total boundary length of geometric shapes. Unlike area, perimeter can be found out of objects that are not closed as well. Perimeter is usually found out of the 2D figures and objects. In short in a closed vessel, it is the line that goes across the edge continuously. Since it is a summation, it is measured in unit like centimeters (cm), meter (m) and millimeter (mm).

Volume – It is the space or the width that is present inside a closed surface. For example, the total space occupied inside a closed room or a cylinder along with its height or depth. It is a 3D measurement and its SI unit is cubic meter.

Curved Surface Area– This is a special type of surface area. The objects have curved surface all around it like eggs, pipes and ball. For non-regular objects, it may be required for finding out area under the curve in the surface. In such cases, top or the base is completely ignored.

Lateral Surface Area– It is computed as complete area measured among lateral surfaces for any given object. In simple words, the surfaces that cover the object are measured and their area is found out together. This total area of the surfaces comprises of this area.

Total Surface Area– In this every possible surface be it inside, outside or enclosed is considered and added together. The total area of the cumulative surface region is termed as the Total Surface Area.          

Formulas

The basic formulas in mensuration for some 2D shapes are as follows.

For a rectangle which has length ‘l’ and width ‘b’, its area notation ‘A’ is given as: $A=l\times b$

Its perimeter ‘P’ is given as: $P=2\left(l+b\right)$

For a square, $l=b$. That is, in a square both the length and breadth are equivalent.

Hence, Area = $l\times l=l^2$,

Perimeter = $4\times l$.

For a triangle, the area is given as

Here, ‘h’ is the height and ‘b’ is the base of a triangle.

$P=\left(a+b+c\right)$

Here, ‘a’, ‘b’ and ‘c’ are the sides of the triangles.

The basic mensuration formulas for some 3D shapes are as follows:

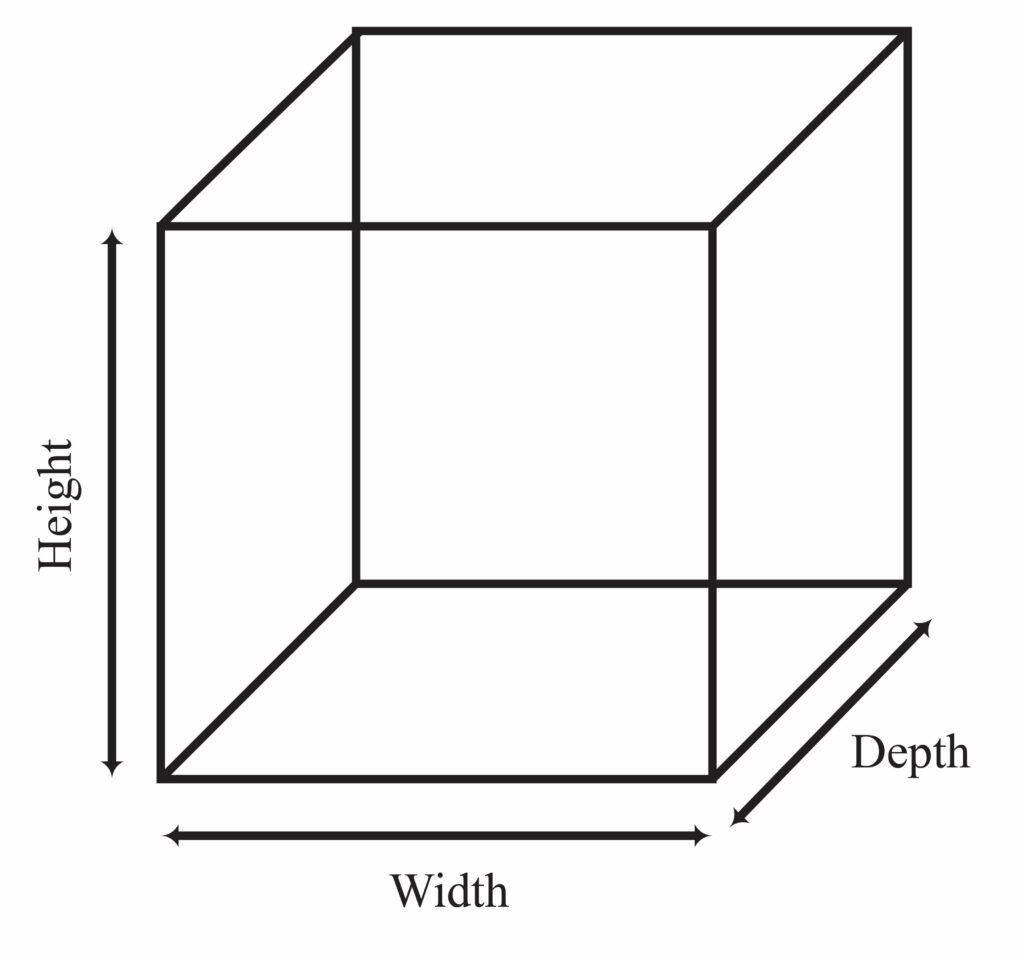
For a cuboid which has ‘l’ length, ‘w’ width and ‘h’ height, its volume ‘V’ is given as:Volume = $l\times w\times h$

Total Surface Area is given as, $2\left(l\times w\right)+2\left(w\times h\right)+2\left(h\times l\right)$

Lateral Surface Area is given as, $2h\left(l+w\right)$

For a cube, $l=w=h$. That is, the length, the width and the height are equal.

Hence, Volume = $l\times l\times l=l^3$

Total Surface Area is given as, $2\left(l\times l\right)+2\left(l\times l\right)+2\left(l\times l\right)=2l^2+2l^2+2l^2$ $$=6l^2$$

Lateral Surface Area is given as, $2l\left(l+l\right)=2l\left(2l\right)$ $$=4l^2$$

Real-Life Applications      

Mensuration is the branch of study in mathematics which is highly important as most of the real-life scenarios is guided by its principles. The major needs are listed below-          

1. In agriculture, mensuration helps in the measuring the dimensions of the field. Also, the total area of the floor that is considered for either selling or purchasing transactions are also found out by this.          
2. Using right angles in corners of structures makes it easier to measure the dimensions.        
3. In the food industry, it is important for measuring the food volumes. For example, when any edible food items are packed, they are carefully measured and packaged according to their weight or volume. In case of liquids like oil or milk, they are directly packaged after measuring their volumes. In this case, mensuration also helps in labelling the optimal cost, since cost is directly dependent on the volume sold.          
4. If it is needed to measure the surface areas of blocks or buildings, mensuration comes into action. For instance, if anyone needs to find out the area of the wall for painting or redecorating purposes, knowing the surface area is important. Moreover, buildings are created and sold according to their surface area as well.          
5. Mensuration allows to know about the changing water levels in natural water bodies such as lakes and rivers. The height and volumes of the different water bodies can also be precisely found out due to this.    

How can one learn this easily?        

It is quite easy to learn about it. One can simply use the different manipulative tools of Math. These include different shaped models such as in nets and solid figures. These shapes can easily impart knowledge regarding the vertices, edges, or faces. The 3D structures can be easily explained in this manner.          

Apart from that, it is also advisable to know about the relations between the units of measurement along with the different conversion rules.

Practice Problem       

1) Find out the area and perimeter of a rectangle with length 10 cm and breadth 4 cm.        

Solution: To find out the area of the rectangle, we use the following formula:      

Area, $A=l\times b$

Therefore, the area of the given rectangle is 10 x 4 = 40 sq. cm

Also, the formula for perimeter of a rectangle is-

Perimeter = 2(l + b)

Therefore, the area of the given rectangle is $10\times 4=40$ sq. cm

Also, the formula for perimeter of a rectangle is-        

Perimeter = $2\left(l+b\right)$

Therefore, the required perimeter is $2\left(10+4\right)$ cm = $2\times 14=28$ cm.

Hence, the area and perimeter of the given rectangle is 40 sq. cm and 28 cm respectively.

2) Find the volume and lateral surface area of a cuboid whose length, width and height is 3cm, 5cm and 9cm respectively.

Solution: To find out the volume of a cuboid, we use the following formula:

Volume of a cuboid, $V=l\times b\times h$

Therefore, the volume of the given cuboid is $3\times 5\times 9=135\text{ cu}\text{.cm}$

Also, the formula for lateral surface area of a cuboid is-        

$\text{Lateral surface area of a cuboid}=2h\left(l+b\right)$

Therefore, the required lateral surface area of a cuboid is

$\text{Lateral surface area of a cuboid}=2\left(9\text{ cm}\right)\left(3\text{ cm}+5\text{ cm}\right)$

$=18\times 8\text{ sq}\text{.cm}$

$\text{Lateral surface area of a cuboid}=144\text{ sq}\text{.cm}$

Hence, the volume and lateral surface area of a cuboid is $135\text{ cu}\text{. cm}$and $144\text{ sq}\text{. cm}$respectively.

3) Find the perimeter of a triangle whose sides are 10cm, 15cm and 12cm.

Solution: To find out the perimeter of a triangle, we use the following formula:

Perimeter of a triangle, $P=a+b+c$

Therefore, the perimeter of the given triangle is $10+15+12=37\text{ cm}$

Hence, the perimeter of the given triangle is $37\text{cm}$.

Context and Applications

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for

• B.Sc Mathematics
• M.sc Mathematics