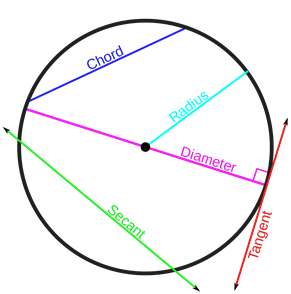
What is meant by tangents in Circles?

A tangent is a line that intersects the circle at only one point and is perpendicular to the radius of a circle. It never invades the interior part of the circle. As it passes at right angles through one point, the Pythagoras theorem is applicable for most of the computations. ‘Tangent’ corresponds ‘to touch’ and in the Latin language, it is said to be ‘tangere’. A circle can have an infinite number of tangents that are always vertical to the radius. The point where the tangent touches the circle is known as the Point of Tangency. There are many applications of tangents in circles. For instance, when a person rides a bicycle, each point on the wheel’s circumference produces a tangent with the road.

The formula for the tangent of a circle

The general equation for the tangent of a circle is given as:

• The tangent to the equation of the circle x² + y² = a² for a straight-line y = mx +c is given by the equation y = mx ± a √ [1+ m²] (‘a’ is the radius of the circle and ‘m’ is the slope of the line).
• The tangent to the equation of the circle, x²+ y² = a² at the points (a₁, b₁) is xa₁ +yb₁ = a² (‘a’ is the radius of the circle and ‘a1’, ‘b1’ are the coordinates of the point).

Hence, the equation of the tangent is expressed as xa₁ + yb₁ = a², where (a₁, b₁) are the coordinates from where the tangent passes through.

Tangent Theorems

• Tangent Radius Theorem: It states that the tangent at any point on the circle lies at 90 degrees through the point of contact. When the point of contact and the center of the circle is connected, the radius of the circle is formed.

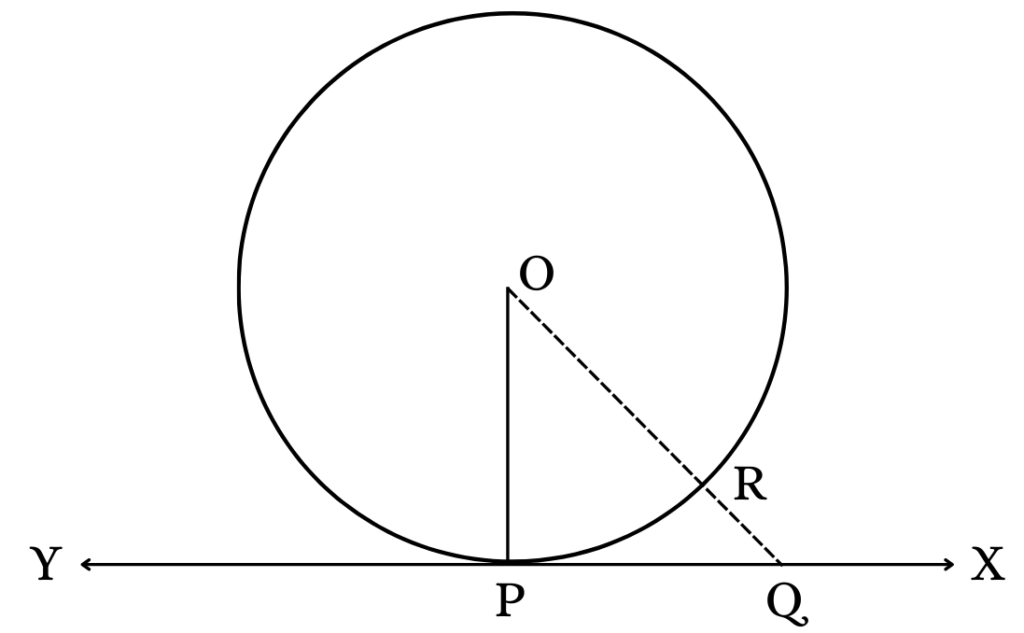
Given: A circle with a center at ‘O’ and tangent XY at ‘P’

Prove: OP is perpendicular to XY

Solution:

Assume any point ‘Q’ on the line XY and join points ‘O’ and ‘Q’ to form a line OQ. Consider ‘R’ to be the point where line OQ makes contact with the circle.

Thus, OQ > OR (from Figure 1)

And, OQ > OP (since OP = OR radius)

Hence, the above case would be the same for all the other points like ‘R’ plotted on the circumference of the circle and joined with its center. So, here OP will be the smallest line that joins XY and the smallest line is always the perpendicular.

• Two Tangents Theorem: It implies that if two tangents are obtained from one point outside the circle, then they will produce tangent line segments equal in length. A tangent line segment is a line connecting to the exterior point and the point of contact (point of tangency).

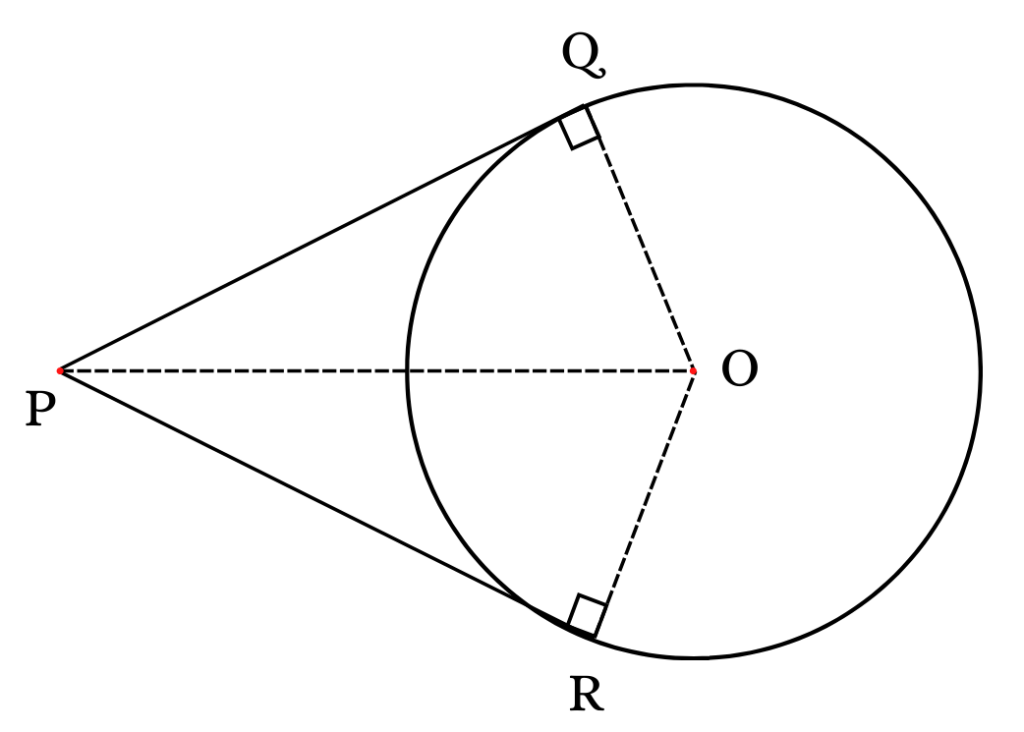
Given: A circle with ‘O’ as its center and point ‘P’ outside the circle. Lines PQ and PR be the tangents having a point of tangency at points ‘Q’ and ‘R’ respectively.

Prove: PQ = PR

Construction: Connect OQ, OR, and OP.

Solution:

OQ is perpendicular to PQ (according to the Tangent Radius Theorem), ∠ OQP = ${90}^0$

So, △ OQP is a right-angled triangle.

Similarly,

OR is perpendicular to PR (according to the Tangent Radius Theorem), thus, ∠ ORP = 90 degree

So, △ ORP is a right-angled triangle.

By using the Pythagoras theorem, which is (Hypotenuse)² = (Height)² + (Base)²

In △ OQP,

OP² = PQ² + OQ²

OP² – OQ² = PQ²

Therefore, PQ² = OP² + OQ² ………………... (1)

In △ ORP,

OP² = PR² + OR²

OP² = PR² + OQ² (since OQ = OR, both are radius)

OP² – OQ² = PQ²

Therefore, PQ² = OP² + OQ² ………………... (2)

From (1) and (2), we get,

PQ² = PR²

Hence, PQ = PR

Tangent Properties

• A tangent intersects a curve at only one point on its periphery.
• A tangent is a line segment that never invades the interior section of the circle
• The tangent touches the radius of the circle at the point of tangency perpendicularly.
• An angle is created with a chord and a tangent together, and this angle is similar to that of the tangent inscribed on the opposite side of the chord.
• From the same external point, the tangent segments to a circle are equivalent.
• The lengths of two tangents from an exterior point to a circle are equal.
• According to the two tangents theorem, both tangents will also subtend equal angles at the center of the circle
• The angle in between the tangents gets bisected by the line linking the external point as well as the center of the circle.

Conditions of Tangency

Based on the point of contact and what is its position to the circle, we can obtain the conditions for the tangent as:

• When the point lies inside the circle

Consider the point P within the circle in Figure 3, where all the lines intersect the circle at two points when they pass through the point P. Thus, it can be said that when any point lies inside the circle, no ‘tangent’ can be made to a circle. So, we can observe that all the lines, which pass through P, are intersecting the circumference of the circle at two points.

• When the point lies on the circle

From the above Figure 4, it can be summarized that it is possible to draw only one tangent through a point P, which lies on the circumference of the circle.

• When the point lies in the exterior area of the circle

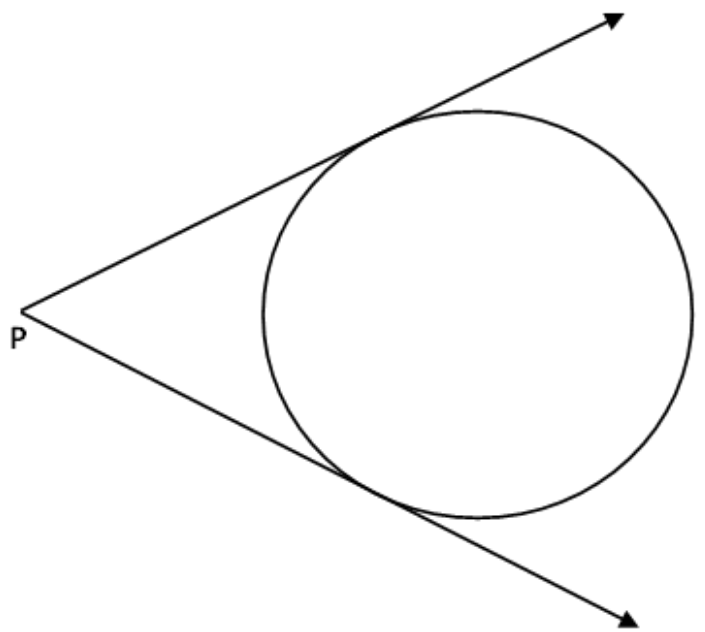
We can interpret from Figure 5 that it is feasible to construct exactly two tangents to a circle from a point that lies outside the circle.

Types of Tangents

A circle is capable of producing an infinite number of tangents. Several lines (secants) can be drawn as tangents to the circle, but all the lines will be able to make contact with the circle at a maximum of two points at one time from the same point. Other lines may not touch the circle at all.

 A line segment that is tangent to more than a single circle is known as a common tangent. The tangents categorized into common tangents are as follows:

• Internal tangents: They are the lines that intersect the line segment joining the centers of both the circles.

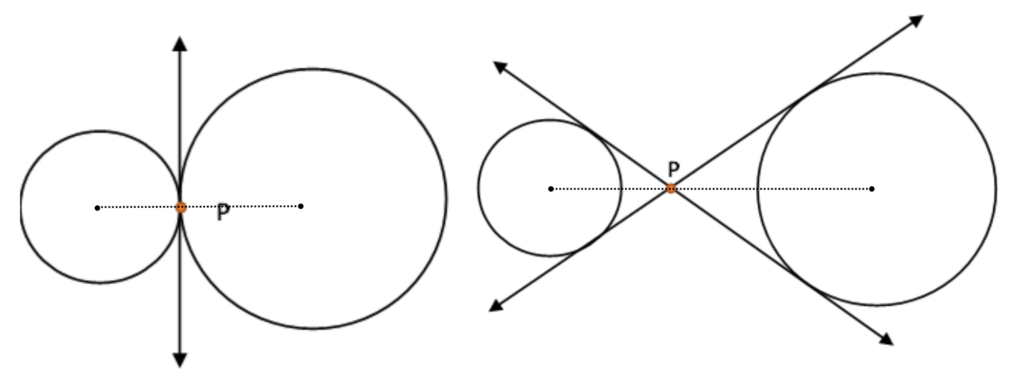
• External tangents: They are the lines that intersect the line segment joining the centers of both the circles.

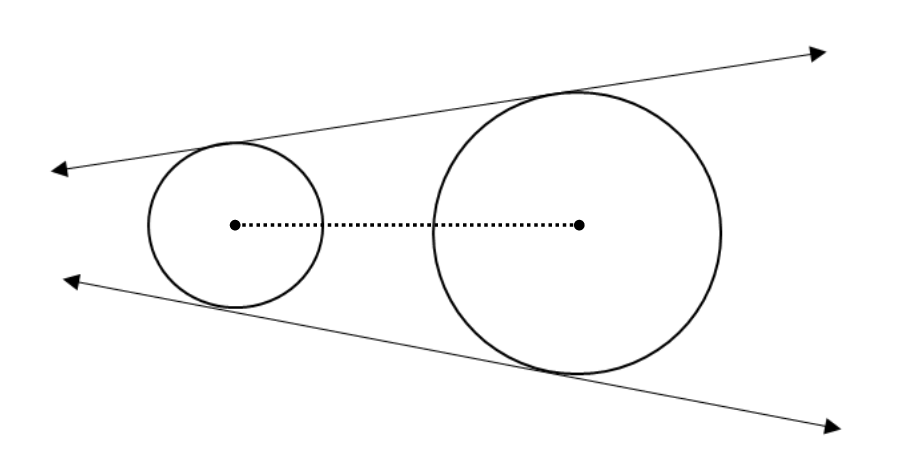
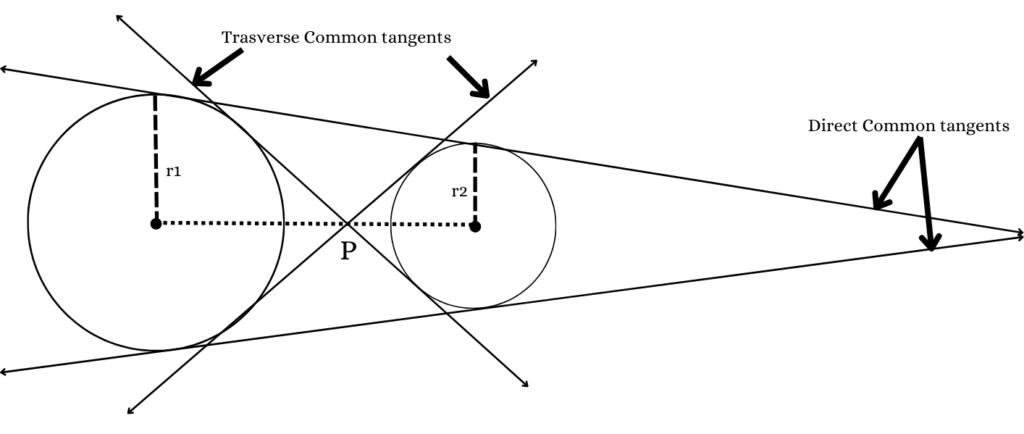
• Direct Common Tangents: The tangents separate externally in the ratio of the radii (r1 and r2) and converge on the line of centers of the circles
• Transverse Common Tangents: The tangents divide internally in the ratio of the radii (r1 and r2) and join on the line of centers of the circles

Real-Life Applications of Tangents

A lot of research on tangents is required since it permits us to determine the slope or inclination of a curved function at a particular point. It is relatively simpler to find the slope of a line, but in the case of finding out the inclination in a curved structure, a thorough study of tangents in circles is necessary. Other areas where tangents are useful in sectors are architecture, differentials and approximations, and engineering and construction industries.

Context and Applications

• Bachelor of Technology (Engineering)
• Masters in Science (Algebra, Geometry, and Cryptography)
• Masters in Science (Mathematics and Applications)

Related Concepts

• Analytical tangents in curves
• Tangential components
• Osculating curve
• Newton’s methodology

Practice Problems

Q1. What is meant by the word ‘Tangent’ in Latin?

1. tangere
2. tang
3. tan cent
4. tenant

Correct Option: a

Explanation: The word ‘Tangent’ in Latin means tangere.

Q2. How many tangent(s) can a circle have?

1. one
2. infinite
3. three
4. four

Correct Option: b

Explanation: A circle can have an infinite number of tangents.

Q3. Which theorem states that the tangent at any point on the circle lies at 90 degrees through the point of contact?

1. Tangent radius theorem
2. Two tangents theorem
3. All of the above
4. None of the above

Correct Option: 1.

Explanation: The tangent radius theorem states that the tangent at any point on the circle lies at 90 degrees through the point of contact.

Q4. How many tangent(s) can be drawn if a point lies outside the circle?

1. none
2. one
3. two
4. infinite

Correct Option: c

Explanation: Two tangents can be drawn from the point that lies outside the circle.

Q5. Which types of tangents do not pass through the center of the two connected circles at one point?

1. Internal tangents
2. External tangents
3. Direct Common Tangents
4. Transverse Common Tangents

Correct Option: b

Explanation: External types of tangents do not pass through the center of the two connected circles at one point.