What are Counting Principles? 

In statistics, the counting principle can be said to be the concept in which the quantity of an item is determined. There can be a single item, or a group of items, or items that are related to each other. In every possible set of items, the quantity of the possible item groups or their sorting measures can be determined with counting principles. 

What is the Fundamental Principle of Counting? 

According to the fundamental principle of counting, the total number of ways for finishing or grouping two tasks is found out. For instance, if we have ‘p’ ways by which we can do one job, and ‘q’ ways of finishing another job, then upon the completion of both ‘p’ and ‘q’ tasks, the job will be completed as a whole. Also, there will be ‘p x q’ number of total ways by which the job can be finished. Upon finishing the task in ‘p x q’ number of ways, the task will be completed in a specified order. 

The fundamental counting principle, or FPS, in short, can be used for quantifying any task or any combination of tasks. Every possible way that exists by which the task can be completed will be included while using the fundamental principle of counting. 

When there is a large group of numbers, it is not usually possible to count each of the items and their combinations individually. With the help of the fundamental counting principle, we can still count the successful ways of performing the tasks while not actually counting them individually. Thus, this is a much more convenient and time-saving process for counting successful ways of doing any given task. 

What do we Mean by the Addition in the Counting Principle? 

The counting principle further has an additional principle in it. Just like the normal counting principle, this also helps in estimating the number of ways by which one task can be completed with respect to another task. 

Let us use an example to demonstrate the addition counting principle. We consider two events, H1 and H2. These two events are chosen so that they are mutually exclusive to each other. By mutually exclusive events, we mean that there will be no common outcomes between H1 and H2. Let ‘p’ be the number of ways by which H1 can be completed separately. Similarly, let ‘q’ be the number of ways by which H2 can be separately completed. In such a scenario, the total number of ways in which the tasks H1 and H2 can both be completed is equal to ‘p+q’. It is similar to the normal counting principle, but we have the sum of the individual ways for successfully completing each task. 

For any number of events, the addition counting principle holds. If more and more tasks are considered, then the events can be counted together by the extension of this addition counting principle. 

What are the Types of Counting Principles? 

The following are the types of counting principles- 

• Stable-order 
• Cardinality 
• Order irrelevance 
• Subitizing 
• Movement is magnitude 
• One-to-one correspondence 
• Conservation 
• Abstraction 
• Hierarchical inclusion 
• Unitizing 

What are the Real-Life Applications of Counting Principles? 

When a word in any language is created, it is made by various combinations of letters. The branch of science that deals with this is known as lexicography. In lexicography, the counting principle is widely used. The most common use of this principle is found in dictionaries. In a dictionary, each word is arranged as per their alphabets. Words starting with the same letters are arranged accordingly. In such cases, the counting principle is used for finding the position of any given word that is present in the dictionary. 

How is the Counting Principle Used? 

If we consider the example of dictionaries, the letters are arranged by various permutations and combinations between them. As per the determination of any word in the dictionary, its rank is first found out. The rank of a word is found out from its letters by the use of permutation procedures. 

What do we Mean by Permutation and Combination? 

The basic counting principle is based on the concept of permutation and combination. In general, we can be easily confused by these two terms as the working of these is quite similar. To avoid confusion, let us take a look at them separately. 

Combination 

By the term combination, we mean the number of ways in which multiple items or objects get mixed together. The process of combination is used for selecting one of the specified combinations among the group of all possible combinations between two or more objects. These objects can be similar or can be completely different from each other. 

In combination, the sequence of the selection of the items does not matter. It means that if two objects get selected, then whether the 1^st object got selected before the 2^nd object, or the 2^nd object got selected before the 1^st one does not matter. In calculation, the order of selection can be ignored. The combination is mainly used for selecting items or members from a collection, group, or committee. 

The formula of combination is given by:

${}^{n}C{}_r=\frac{n!}{r!\left(n-r\right)!}$

Here, the term ‘ⁿC_r’ denotes the total number of combinations. The term ‘n’ denotes the total number of items present in the group, while ‘r’ denotes the chosen number of items from the group. 

Permutation 

The term permutation is different from the combination. Even though the basic idea is still the same, the major difference between permutation and combination is that the order in which the objects are selected is important in permutation. 

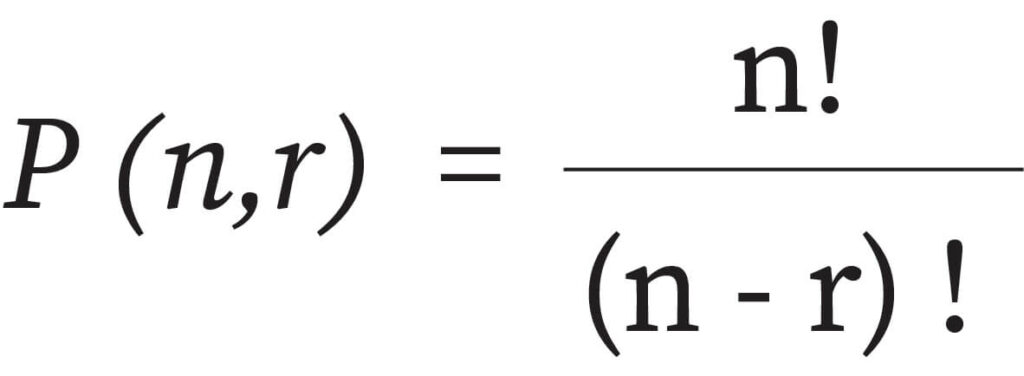
The process of permutation results in the arrangement of the different items. However, the arrangement process takes place alongside ordering. If two objects ‘a’ and ‘b’ are chosen, then (a, b) and (b, a) will be counted separated in permutation. 

The formula of permutation is given by 

${}^{n}P{}_r=\frac{n!}{\left(n-r\right)!}$

Here, the term ‘ⁿP_r’ denotes the total number of permutations. The term ‘n’ denotes the total number of items present in the group, while ‘r’ denotes the chosen number of items from the group. 

Formulas 

The formula for the number of ways of selection of r objects from a group of n objects is ${}^{n}C{}_r=\frac{n!}{r!\left(n-r\right)!}$.

The formula for the number of ways of arrangement of r objects from a group of n objects is ${}^{n}P{}_r=\frac{n!}{\left(n-r\right)!}$.

Practice Problem 

• Find out the possible ways in which an employee can have his/her lunch in the canteen when there are 3 choices in starters and 9 choices for the main course. 
  • Using the fundamental counting principle, we have 3 starter choices and 9 main course choices. 

Therefore, the total number of ways in which the lunch can be done is 3×9=27 ways. 

• If there are 5 books in a library, and you can take only two books, then in how many possible ways can you select the books, considering the order is not important? 
  • If the order of selection is not important, we will use a combination to solve this problem. 

Since there are 5 books in total and we can select only 2 books, therefore n = 5, and r = 2. 

Using the formula for combination, we have 

${}^{5}C{}_2=\frac{5!}{\left(2!\left[\left\{5-2\right\}!\right]\right)}$

${}^{5}C{}_2=\frac{5!}{\left(2!\times 3!\right)}$

${}^{5}C{}_2=\frac{120}{\left(2\times 6\right)}$

${}^{5}C{}_2=\frac{120}{12}$

${}^{5}C{}_2=10$

Therefore, we can select two books among five in 10 different ways, when the order is not important. 

Context and Applications    

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for: 

• Bachelor of Science in Mathematics 
• Master of Science in Mathematics