What are Angles?

In mathematics, angles constitute a very important part. Just like the concept of lines, an angle is a necessary figure that is used for measurement. How do you define its formation? It is formed when two or more lines meet at a point. The point at which two or more lines meet is known as the vertex. When the lines get inclined at this point, they do form various angles. Angles are measured from the vertex in terms of degrees.

What is the Origin of Angle?

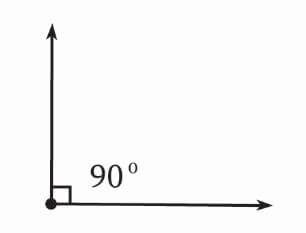
In ancient Greek and Latin study, people found the core for the measurement of various objects that are fixed to a point. To measure this inclination, the term ‘angulus’ was used. This basically stated how the vertex or corner was used to measure the sides that are having that corner as their common intersection point. The properties and various classifications of angles are discussed below.

Real-Life Application

In geometry, the idea of measuring inclinations among various objects is extended further. In real-life, different slopes and planes are created after calculating the optimum angle requirement. In geography, the measurement of angles are mainly used for finding latitude and longitude. There are many types present and they can be categorized on many different parameters.  The main classification is usually based on their measurements or based on their co-relationship with each other. Both types can further be subdivided. Using the Javascript, we can find the angle between two points. They are discussed below.

Types based on their Measurements:

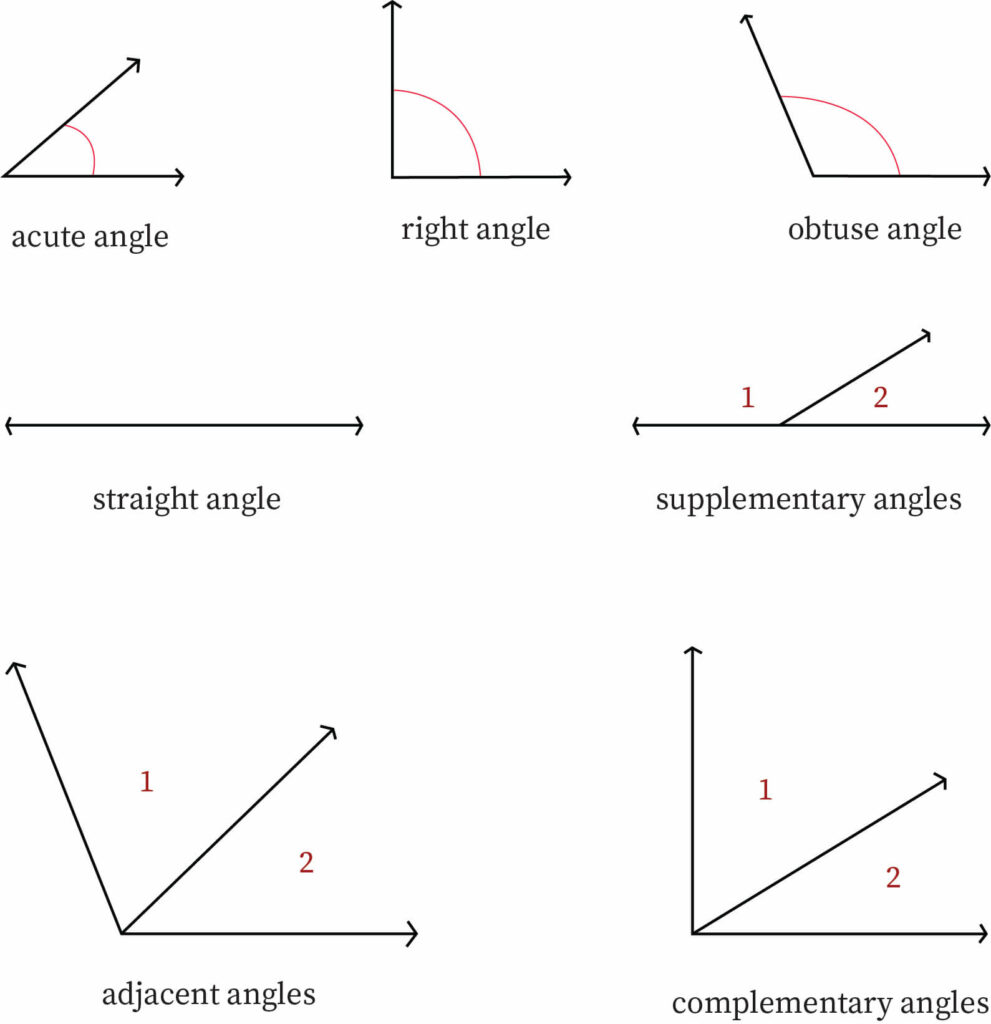
Acute Angle

This is the smallest of all other angles when it comes to measurement. It lies between 0 and 90 degrees. In other words, it is always less than 90 degrees.

Right Angle

If the value of an angle is exactly 90, then this is called a right angle. Here, the two lines intersecting to form the angle are always perpendicular.

Obtuse Angle

An angle that has a value greater than 90 yet less than 180 degrees is called an obtuse angle. The value of this angle is always greater than a right or an acute angle. Also, if an acute and a right angle are added, their combined result gives rise to an obtuse angle.

Straight Angle

It is an angle around a straight line. Its value is 180 degrees. It is formed when two right angles are together.

Reflex Angle

The value of a reflex angle lies between 180 and 360 degrees. If a straight line is measured in all four coordinates, the total angle measured is 360. Any angle less than that value but more than a straight angle is called a reflex angle. The addition of an obtuse with a right angle will result in the formation of a reflex angle.

Angles Based on their Relation

It has been classified according to their correlation with one another. An angle is formed when a ray is rotated about its endpoints. On drawing this in a paper, the angle between the initial and final point forms an arc.

Adjacent Angles

Two angles, which have the same vertex, and point towards the same direction or side without forming any overlapping angle, are known as adjacent angles. There are normally no common interior points between a pair of adjacent angles. Also, there is a set of non-common arms for adjacent angles.

Complementary Angles

When the summation of two angles is exactly equal to a right angle, or 90 degrees, then the two angles are said to be complementary to each other. Both the angles are known as each other’s complement.

Supplementary Angles

If two angles add up to form exactly 180 degrees in total, then both are called as supplementary angles to each other. A pair of supplementary angles which add up together to form a straight angle, is known as a linear pair. Linear pairs are always supplementary in nature.

Vertically Opposite Angles

Intersection of two lines forms four angles, where two pairs of vertically opposite angles exist. These are placed exactly on the opposite sides of the common vertex. Both vertically opposite angles are always the same in value. If the intersecting lines are not perpendicular to each other, then one pair of vertically opposite angles are obtuse, and another pair is acute.

Formulas

• Angles of polygon

Where, n is the number of sides.

• Angles of right-angle triangle

When the hypotenuse and the length of the opposite are known, the sine function can be used

When the hypotenuse and the length of the adjacent sides are known, the cosine function can be used

When the length of the adjacent side and opposite side are known, the tangent function can be used

What are the Conditions for Parallelism?

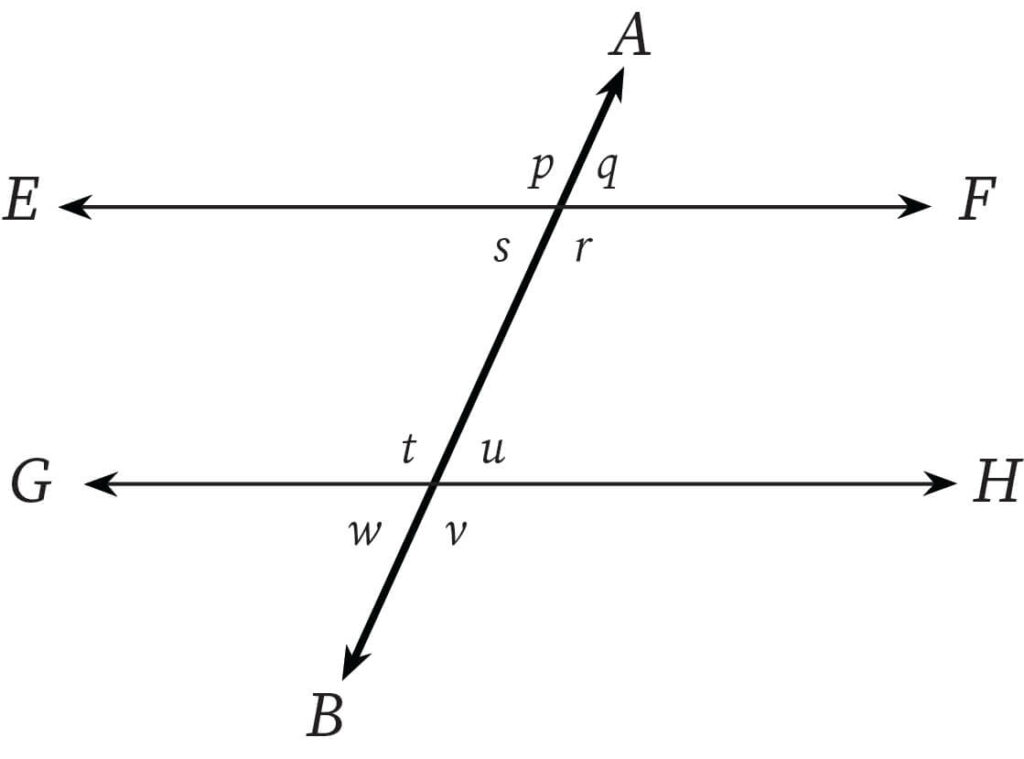
In some specific set of conditions, the criterion for parallelism is satisfied. Such conditions occur when two or more parallel lines are cut through by a transversal line. In such cases, we observe the following conditions

• A pair of corresponding angles are always equal in value.
• The value of a pair of alternate interior angles are found to be exactly equal.
• The transversal line cuts the parallel lines into two different regions.

Basically, the conditions for two lines to be parallel in nature can be explained from the following:

• When the corresponding angles are exactly equal in value.
• When the alternate interior angles have the same value.
• When the interior angles on the same side of the transversal are supplementary the lines are parallel.

Practice Problem

In the above diagram, if p = 70 degrees and u = 110 degrees, find the rest of the angles. As p = 70 degrees, r will be 70 degrees as well. This is because they are vertically opposite.

Also, s = 180 - 70 degrees = 110 degrees, as p and s lie on the same straight line.

Therefore, q = 110 degrees as well, as it is vertically opposite to s.

Similarly, w = u = 110 degrees, as w and u are vertically opposite.

Also, t = 180 - 110 degrees = 70 degrees , as t and u lie on the same straight line.

As a result, v = 70 degrees since v and t are vertically opposite to each other.

Context and Applications

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for

• B.Sc. in Mathematics
• B.Sc. in Physics
• M.Sc. in Mathematics