What is a Ratio?
A ratio is a comparison between two numbers of the same kind. It represents how many times one number contains another. It also represents how small or large one number is compared to the other.
How are Ratios Expressed?
In a ratio, the comparison between numbers is shown using division. Ratios can be represented in many forms. Consider two numbers x and y. The ratio between x and y can be represented as:
- the ratio of x to y
- x is to y
- x:y
- x/y
Generally, the representation "x:y" is used. The first number in a ratio is the antecedent, and the last number is the consequent. Hence, in the above example, x would be the antecedent and the y would be the consequent. In a ratio, all the entities must have the same units.
Types of Ratios
There are two types of ratios: part-to-part, and part-to-whole.
- A part-to-part ratio represents how two different entities are related to each other.
- A part-to-whole ratio shows how one entity is related to the whole system.
For example, a city contains x number of people below the age of 18 and y number of people above the age of 18. Hence, the ratio of people below the age of 18 to the people above the age of 18 in the city would be x:y. The ratio of people below the age of 18 to the total number of people in the city would be x:(x+y). Here, x:y is a part-to-part ratio, and x:(x+y) is a part-to-whole ratio.
Procedure for Finding the Ratio
Consider a case where the ratio between two entities needs to be found in a given problem. The following are the steps to find the ratio between the two entities:
- First, the quantities or values of both the entities whose ratios need to be determined are identified or calculated.
- Next, they are written in the form of a fraction.
- The fraction is then simplified if possible and the final ratio is obtained.
For example, there are 30 boys and 15 girls in a class of 45 students, and you are asked to find the ratio of girls to boys in the class. Following the above steps:
- The two entities are 15 and 30.
- Now, 15 and 30 will be written as a fraction: 15/30.
- The fraction can be further simplified to 1/2. Hence, the final ratio obtained is 1:2, so the ratio of girls to boys in the class will be 1:2.
Properties of a Ratio
Consider the ratio of two numbers, m and n. It will have the following properties:
- If m = n, then the ratio between m and n will be equal to 1 (m:n = 1).
- If m>n, then the ratio between m and n will be greater than 1 (m:n > 1).
- If m<n, then the ratio between m and n will be lesser than 1 (m:n < 1).
- A ratio remains the same if both the antecedent and consequent are multiplied or divided by the same non-zero number.
- Two ratios can be compared just like real numbers.
Ratios in Triangles
Ratios play a significant role in triangles. Ratios are used in right-angled triangles to find the trigonometric functions and sides, in similar triangles to find the areas and the sides of the triangles, and so on.
Ratios in Right Triangles
In a right-angle triangle, one of the three angles is equal to 90 degrees. The image below shows a right-angled triangle.
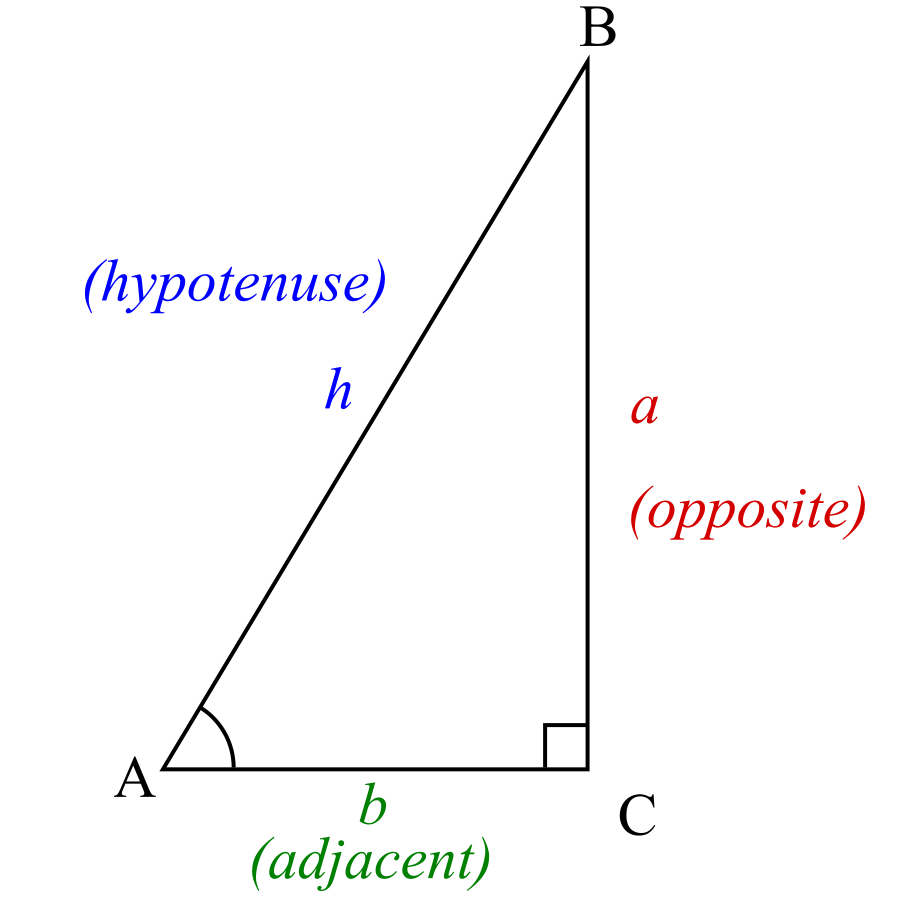
In the above triangle, consider angle A as a reference angle. Hence, the side BC will be the opposite side, and the side AC will be the adjacent side. The side AB is the hypotenuse. Hence, the trigonometric identities sine, cosine, and tangent can be found for the given triangle.
For the right-angle triangle ABC given above, the trigonometric ratios can be calculated using the following formulas:
Ratios in Similar Triangles

Two triangles are said to be similar if one of the triangles can be obtained by scaling another one to a certain factor. There are three tests to identify whether the triangles are similar or not. The tests are the SSS test, SAS test, and AA or AAA test.
- According to the SSS test, if all the three sides of one triangle are in an equal proportion to all the corresponding three sides of another triangle then, the triangles are said to be similar.
- According to the SAS test, if any of the two sides and one angle of a triangle are in equal proportion to the corresponding two sides and one angle of another triangle, then the triangles are said to be similar.
- According to the AAA or AA test, if all the three angles or two angles of one triangle are equal to the corresponding angles of another triangle, then the triangles are said to be similar.
Ratios are also used in similar triangles to find the areas of the triangle.
Formulas
For any right-angled triangle having ,
For any triangles and ,
Context and Applications
Ratios are used on a daily basis in various fields and also in day-to-day life. One real-life examples of ratios is cutting a pizza in the ratio of 1:4 for 4 people. You can also find the ratios of:
- One type of fruit to another
- One type of fruit to the total fruits in a basket
- The average speed to the top speed of a bike
- And so on
Ratios are useful for students studying various undergraduate and postgraduate courses, such as Bachelors or Masters in Engineering; B.S. in Mathematics, Physics, and Chemistry; and Masters in Science, Mathematics, Physics, and Chemistry.
Practice Problems
1. Which of the following is the comparison of one or more numbers?
a. Similarity
b. Ratio
c. Multiplication
d. Factorization
Answer: b
Explanation: A ratio is the comparison of one or more numbers. Similarity is the term used when two shapes are similar, meaning they are the same in shape and size. Multiplication is the product of two numbers, and factorization is the process of finding out the factors of numbers.
2. Which of the following ratios represent how two different entities are related to each other?
a. Part-to-part ratio
b. Part-to-whole ratio
c. Whole-to-part ratio
d. Factorized ratio
Answer: a
Explanation: A part-to-part ratio represents how two different entities are related to each other. The rest of the given ratios do not represent how two different entities are related to each other.
3. Which of the following in a right-angled triangle is the ratio of the opposite side and the hypotenuse?
a. Sine of any angle
b. Cosine of any angle
c. Tangent of any angle
d. Cot of any angle
Answer: a
Explanation: The sine of any angle in a right-angled triangle is the ratio of the opposite side and the hypotenuse. The cosine of any angle in a right-angled triangle is the ratio of the adjacent side and the hypotenuse. The tangent of any angle in a right-angled triangle is the ratio of the opposite side and the adjacent side. The cot of any angle in a right-angled triangle is the ratio of the adjacent side and the opposite side.
4. Which of the following is not a test to identify whether triangles are similar or not?
a. SSS test
b. SAS test
c. AA test
d. SA test
Answer: d
Explanation: SA test is not a test to identify whether triangles are similar or not. SSS test, SAS test, and AA test are the tests to identify whether triangles are similar or not.
5. Which of the following ratios represent how one entity is related to the whole system?
a. Part-to-part ratio
b. Part-to-whole ratio
c. Whole-to-part ratio
d. Factorized ratio
Answer: b
Explanation: A part-to-whole ratio represents how one entity is related to the whole system. The rest of the given ratios do not represent how one entity is related to the whole system.
Want more help with your trigonometry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.