What is a Sinusoidal Function?
The family of sinusoidal functions applies to either sine or cosine waves since they are the same except for a horizontal change.
The set of X coordinates of the unit circle is the cosine function, and the set of Y coordinate is the sine function.
NOTE: All sine and cosine functions are periodic. A periodic function can be a sinusoid. This is because a periodic function involves sin, cosec, cos, sec, tan, and cot, while sinusoidal functions only involve sin or cos.
Sinusoidal Wave
The graph for the ‘sine’ or ‘cosine’ function is called a sinusoidal wave.
The standard equation to find a sinusoid is:
y = D + A sin [B (x - C)] or
y = D + A cos [B (x - C)]
where,
- A = Amplitude
- B = No of cycles from 0 to 2π or 360 degrees
- C = Phase shift (horizontal shift)
- D = Sinusoidal axis
- Period = 2π/B
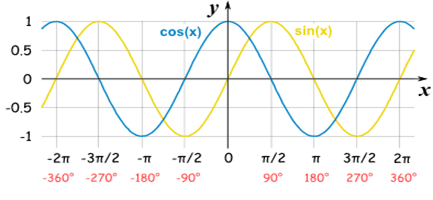
Properties of Sinusoidal Functions (Layman’s Terms)
- Period: The period of a sinusoidal wave is the length of a whole cycle.
- Frequency: The number of whole cycles that occur every second.
- Amplitude: The vertical distance between the sinusoidal axis and the maximum or minimum value of the function.
- Phase Shift: It designates the time difference between two similar signals.
- Sinusoidal Axis: The horizontal line lying between the crests and the troughs of the graph of the function.
Characteristics of Sine and Cosine Functions
The sine and cosine functions have several distinct characteristics:
- They are periodic functions with a period of 2π.
- The domain of each function is (−∞,∞), and the range is [−1,1].
- The graph of y = sin x is symmetric about the origin because it is an odd function.
- The graph of y = cos x is symmetric about the y-axis because it is an even function.
Period, Amplitude, and Midline
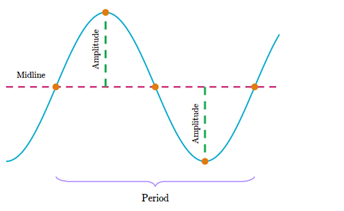
- Midline: The horizontal that line passes precisely between the maximum and minimum points of the graph in the middle.
- Amplitude: It is the vertical distance between one of the extreme points and the midline.
- Period: The difference between two maximum points in succession or two minimum points in succession (these distances must be equal).
How to Calculate the Period of a Sinusoidal Function?
The general equation of the sine function,
y = D + A sin [B (x - C)]
The equation that shows the relation of B to the period is given as P = 2π|B|. If |B|>1, then the period is less than 2π, and the function undergoes a horizontal compression, whereas if |B| < 1, then the period is greater than 2π and the function undergoes a horizontal stretch.
For example,
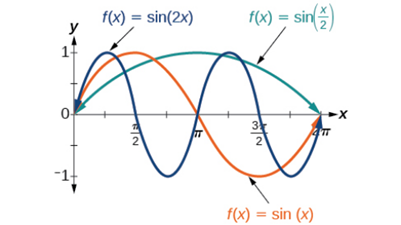
- f(x) = sin (x), B = 1, so the period is 2π, which we knew.
- If f(x) = sin (2x), then B = 2, so the period is π and the graph is compressed.
- If f(x)= sin (x2), then B=12, so the period is 4π and the graph is stretched. Notice in the below figure how the period is indirectly related to |B|.
How to Determine the Amplitude of Sinusoidal Function?
For a sinusoidal function, returning to the general formula,
y = D + A sin [B (x - C)]
We have learned how the variable B refers to the period. Now let’s switch to variable A to evaluate how the amplitude, or the most significant distance from the others, is connected.
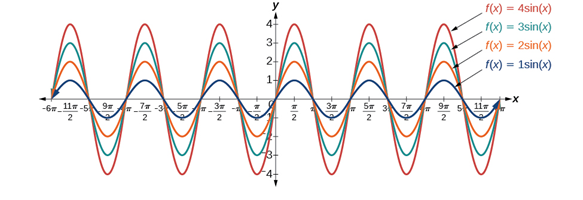
A represents the vertical stretch factor, and the amplitude is its absolute value |A|. Thus, the local maxima will be a distance |A| above the vertical midline of the graph, which is the line x = D; because D = 0 in this case, the midline is the x-axis.
The local minima will be the same distance below the midline.
If |A| > 1, the graph is stretched.
For example, the amplitude of f(x) = 4 sin x is twice the amplitude of f(x) = 2 sin x.
If |A| < 1, the graph is compressed.
Finding Features from the Graph
We can analyze it to find the midline, amplitude, and time provided in the graph of a sinusoidal function. Consider the following graph, for instance.

The sine wave in the graph has a maximum point at (1,7), then a minimum point at (3,3), and then a further maximum point at (5,7).
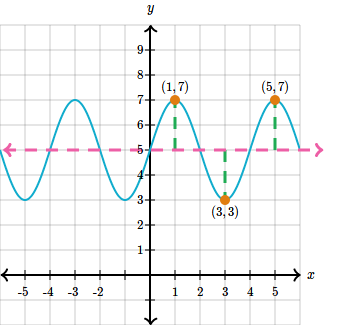
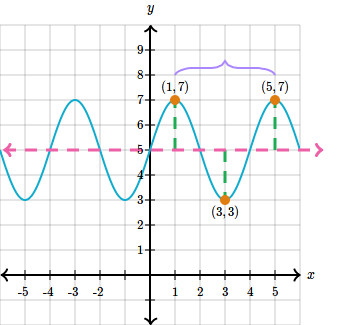
The horizontal line that passes exactly between Y=7 (the maximum value) and Y=3 (the minimum value) is Y=5, so that’s the midline.
The vertical distance between the midline and each of the extremum points is 2, so the amplitude is that.
The interval between the two maximum points in succession is 4, so that’s the period.
We know that without altering its shape, a sinusoidal wave propagates. To study wave propagation in the distributed linear method, sine waves are used.
Frequency
The concept of frequency is used in some applications of periodic phenomena instead of the period.
The number of periods (or cycles) per unit of time is the frequency of a sinusoidal function.
Since frequency is the number of cycles per unit time and the amount of time to complete one cycle is the period, the equation that shows the relationship between frequency and time is as follows:
frequency = 1/period
Formulas
It the equation of a sinusoidal function is y = D + A sin [B (x - C)], then the following formulas hold:
- Period = 2π|B|
- Amplitude = |A|
- Frequency = 1/period = |B|2π
- Sinusoidal axis: y=D
- Horizontal shift = C units
Common Mistakes
- Degrees vs Radians
In calculus, all the trigonometric calculations are done considering that the angles are specified in radians and not in degree.
- Sin(x) is not multiplication
- Sin (x+y) ≠ Sin (x) + Sin(y)
- Sin 3x ≠ 3 * Sin(x)
- Powers of sine functions
- Sin(xn) ≠ (Sin x)n
- Inverse in Sine function
- Sin-1(x) ≠ 1/Sin(x)
Context & Applications
This concept is applicable for pre-graduation, graduation, and post-graduation students and many engineering branches.
Trigonometry can have applications in:
- Measuring the height of a tall building or a mountain.
- Developing video games.
- Construction industry.
- Archaeological excavation.
Related Concepts
- Cosine
- Trigonometry
Want more help with your trigonometry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Sinusoidal Functions Homework Questions from Fellow Students
Browse our recently answered Sinusoidal Functions homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.